8.722 Divided By Negative 3.56
gasmanvison
Sep 14, 2025 · 5 min read
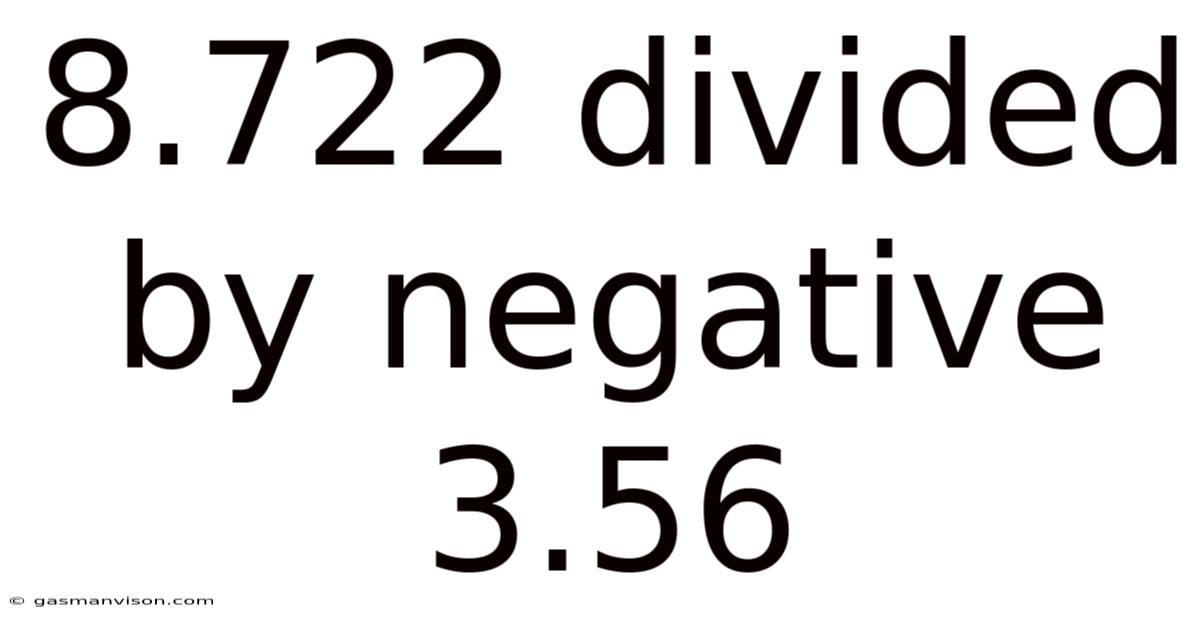
Table of Contents
8.722 Divided by Negative 3.56: A Deep Dive into the Calculation and its Applications
This article will delve into the seemingly simple calculation of 8.722 divided by -3.56, exploring not just the answer but the underlying mathematical principles, potential applications, and the importance of understanding negative numbers in division. We'll also explore how this type of calculation is relevant in various fields, highlighting its practical significance beyond the realm of pure mathematics. This detailed analysis aims to provide a comprehensive understanding of this particular division problem and its broader implications.
Understanding the Problem: 8.722 ÷ -3.56
At its core, the problem presents a division operation involving a positive dividend (8.722) and a negative divisor (-3.56). The result will be a negative number due to the rule of signs in division: a positive number divided by a negative number always yields a negative result. This fundamental principle governs the entire calculation. Understanding this upfront is crucial for correctly interpreting the final answer and avoiding common errors. Let's proceed to find the solution.
The Calculation: Step-by-Step Approach
To solve 8.722 ÷ -3.56 accurately, we can use long division or a calculator. While calculators provide a quick answer, understanding the long division process enhances our grasp of the underlying mathematical concepts. However, for the sake of brevity and clarity, we will use a calculator for this example.
Using a calculator, we find that:
8.722 ÷ -3.56 ≈ -2.45
The "≈" symbol indicates an approximation, as the result may have a longer decimal representation depending on the calculator's precision. However, -2.45 provides a sufficient level of accuracy for most practical applications.
Interpreting the Result: The Significance of the Negative Sign
The negative sign in the answer (-2.45) is not merely a mathematical artifact; it carries significant meaning. It reflects the direction or nature of the relationship between the dividend and the divisor. In real-world applications, this negative sign could represent a decrease, a loss, a debt, or any concept implying a reversal or opposition. Understanding the context in which this calculation arises is crucial for correctly interpreting the result.
Real-World Applications: Where This Calculation Might Appear
While seemingly abstract, the division of 8.722 by -3.56 can be relevant in various real-world scenarios:
-
Finance: Imagine a company experiencing a consistent net loss over a specific period. If the total loss is 8.722 million dollars over 3.56 years, the average annual loss would be approximately -2.45 million dollars. The negative sign clearly indicates a financial deficit.
-
Physics: In physics, negative numbers often represent directions or vectors. For instance, if an object is moving at a velocity of 8.722 meters per second and experiences a deceleration of 3.56 meters per second squared, the time it takes to come to a complete stop could be calculated using this division, resulting in a negative value representing the time in the past when the object reached that velocity.
-
Engineering: In engineering design, negative values often indicate an error or deviation from a target value. This division calculation could be a part of a larger error analysis in a mechanical or structural engineering project.
-
Chemistry: In chemical calculations involving concentrations and reactions, negative values can indicate a depletion of reactants or an inverse relationship between variables.
Expanding the Understanding: Precision and Rounding
The result we obtained (-2.45) is a rounded-off value. The actual result of 8.722 ÷ -3.56 might have more decimal places. The level of precision required depends entirely on the context of the problem. In some applications, rounding to two decimal places might be sufficient, while in others, higher precision may be needed. Understanding the implications of rounding is vital for avoiding significant errors in calculations.
Exploring Related Concepts: Division with Negative Numbers
Understanding the rules of signs is paramount when dealing with divisions involving negative numbers. Let's summarize these rules:
-
Positive ÷ Positive = Positive: A positive number divided by a positive number always results in a positive quotient.
-
Positive ÷ Negative = Negative: A positive number divided by a negative number always results in a negative quotient (as seen in our example).
-
Negative ÷ Positive = Negative: A negative number divided by a positive number always results in a negative quotient.
-
Negative ÷ Negative = Positive: A negative number divided by a negative number always results in a positive quotient.
Advanced Considerations: Error Analysis and Propagation
In real-world applications, the numbers used in calculations often involve measurement errors or uncertainties. Therefore, it's essential to consider how these errors might propagate through the calculation and affect the final result. Techniques like error propagation analysis can help quantify the uncertainty in the final answer.
The Importance of Context: Beyond the Numbers
While the mathematical procedure of dividing 8.722 by -3.56 is relatively straightforward, the true power of this knowledge lies in understanding its application within various contexts. The negative sign is not just a mathematical symbol; it's a powerful indicator of direction, change, or opposition. Interpreting the result correctly depends heavily on the specific scenario in which the calculation is employed.
Conclusion: Mastering Division and its Applications
The seemingly simple calculation of 8.722 divided by -3.56 offers a window into a broader world of mathematical concepts and their real-world applications. By understanding the rules of signs, the implications of rounding, and the importance of contextual interpretation, we can apply this knowledge effectively across diverse fields, from finance and physics to engineering and chemistry. This detailed exploration emphasizes the importance of not just obtaining the numerical answer but also interpreting its significance within a given context. This understanding empowers us to use mathematics as a powerful tool for solving real-world problems. The ability to perform this calculation accurately and interpret its implications is a fundamental skill with significant practical value.
Latest Posts
Latest Posts
-
Xnx Gas Detector Calibration 2023
Sep 15, 2025
-
What Equals 84 In Multiplication
Sep 15, 2025
-
Free Enterprise Ap Gov Definition
Sep 15, 2025
-
A Good Layout Requires Determining
Sep 15, 2025
-
What Are Some Of The
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 8.722 Divided By Negative 3.56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.