8 Divided By 1 3
gasmanvison
Sep 02, 2025 · 5 min read
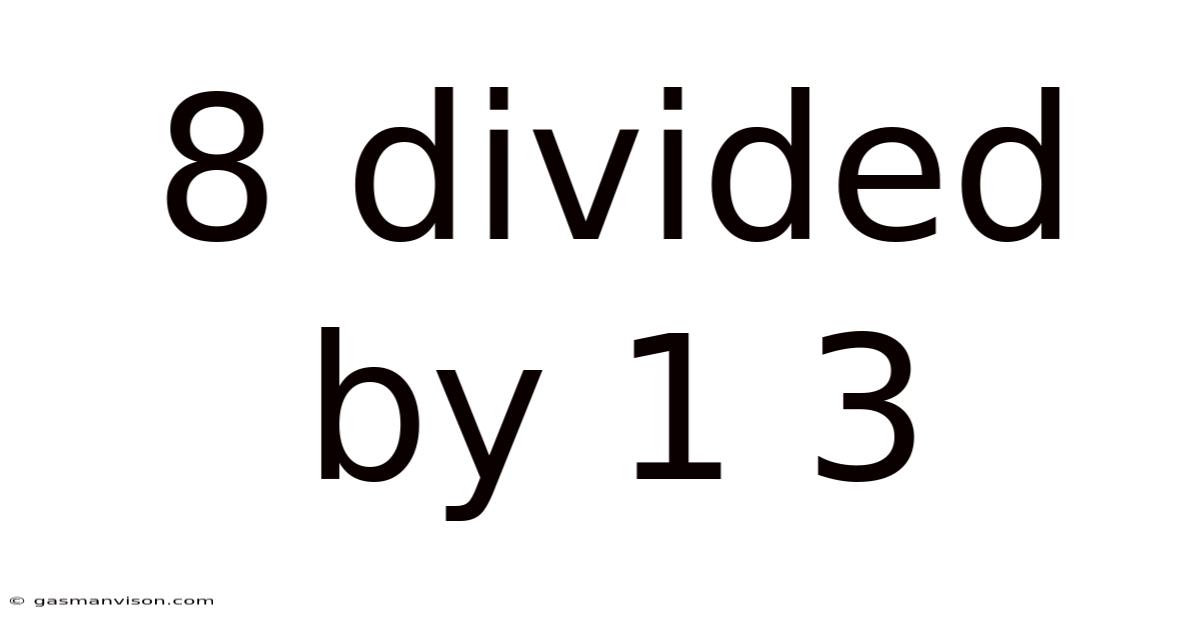
Table of Contents
Decoding 8 Divided by 1⅓: A Deep Dive into Fraction Division
This article explores the seemingly simple yet surprisingly nuanced problem of dividing 8 by 1⅓. We'll move beyond the basic answer to delve into the underlying mathematical principles, explore different solution methods, and uncover the practical applications of this type of calculation. Understanding this seemingly simple division problem provides a strong foundation for tackling more complex fraction problems and enhances your overall mathematical proficiency. This comprehensive guide will equip you with the skills and knowledge to confidently solve similar problems and apply them in various contexts.
Understanding the Problem: 8 ÷ 1⅓
The problem, 8 divided by 1⅓, presents a common scenario in mathematics involving the division of a whole number by a mixed number (a number consisting of a whole number and a fraction). This type of problem requires a strong grasp of fraction manipulation, specifically converting mixed numbers to improper fractions and understanding the process of reciprocal multiplication. The apparent simplicity hides the richness of the underlying mathematical concepts. Let's unravel this step by step.
Method 1: Converting to Improper Fractions
This is the most common and arguably the most efficient method for solving division problems involving fractions. The first step is to convert the mixed number, 1⅓, into an improper fraction.
-
Step 1: Convert the mixed number to an improper fraction. To do this, multiply the whole number (1) by the denominator (3), add the numerator (1), and keep the same denominator. This gives us ⁴⁄₃.
-
Step 2: Rewrite the division problem. The problem now becomes 8 ÷ ⁴⁄₃.
-
Step 3: Invert and multiply. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of ⁴⁄₃ is ³⁄₄. Therefore, the problem transforms into 8 × ³⁄₄.
-
Step 4: Simplify and solve. We can simplify before multiplying. 8 can be divided by 4, resulting in 2. The equation simplifies to 2 × ³⁄₁ = 6.
Therefore, 8 divided by 1⅓ equals 6.
Method 2: Using Decimal Equivalents
While the improper fraction method is generally preferred for its accuracy and avoidance of rounding errors, we can also solve this using decimal equivalents.
-
Step 1: Convert the mixed number to a decimal. 1⅓ is equal to 1.333... (the 3s repeat infinitely). For practical purposes, we can use a reasonable approximation, such as 1.33.
-
Step 2: Perform the division. Divide 8 by 1.33. Using a calculator, this gives an approximate answer of 6.015.
-
Step 3: Consider the limitations. This method introduces a small degree of inaccuracy due to the rounding of the decimal equivalent. The more decimal places you use, the more accurate the result will be, but it also adds complexity.
Method 3: Long Division with Fractions
This method demonstrates the fundamental principles of division in a more visual manner. It is less efficient than the improper fraction method but provides a deeper understanding of the process.
-
Step 1: Express 8 as a fraction. We can rewrite 8 as ⁸⁄₁.
-
Step 2: Perform long division with fractions. This involves dividing ⁸⁄₁ by ⁴⁄₃. To do this, we multiply ⁸⁄₁ by the reciprocal of ⁴⁄₃, which is ³⁄₄.
-
Step 3: Multiply the numerators and denominators. This gives (8 x 3) / (1 x 4) = ²⁴⁄₄.
-
Step 4: Simplify the result. ²⁴⁄₄ simplifies to 6.
Practical Applications: Real-World Scenarios
Understanding fraction division, as exemplified by this problem, has several practical applications in everyday life and various professional fields:
-
Cooking and Baking: Scaling recipes up or down often involves dividing or multiplying fractional quantities of ingredients. For instance, if a recipe calls for 1⅓ cups of flour and you want to make only half the recipe, you'd need to calculate ½ x 1⅓.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Dividing lengths or quantities often involves fractions and mixed numbers.
-
Finance and Budgeting: Dividing budgets, calculating proportions of investments, or determining the cost per unit often involves working with fractions and decimals.
-
Data Analysis and Statistics: Many statistical calculations involve fractions and the manipulation of data expressed as ratios or proportions.
-
Sewing and Tailoring: Calculating fabric requirements or adjusting pattern sizes often requires precise fractional calculations.
Expanding the Understanding: More Complex Problems
The principles used to solve 8 ÷ 1⅓ can be applied to more complex problems involving:
-
Dividing mixed numbers by mixed numbers: The same steps of converting to improper fractions and then inverting and multiplying can be followed. For instance, 2⅔ ÷ 1⅚ would require converting both mixed numbers to improper fractions before proceeding with the calculation.
-
Dividing fractions by whole numbers: This simplifies to multiplying the fraction by the reciprocal of the whole number (which is 1/whole number).
-
Dividing whole numbers by fractions: This involves multiplying the whole number by the reciprocal of the fraction.
Mastering the foundational concepts illustrated in this problem will provide a solid base for tackling more intricate mathematical challenges involving fractions and mixed numbers.
Beyond the Calculation: Developing Mathematical Intuition
While obtaining the correct answer (6) is essential, understanding the underlying principles is equally crucial. The ability to confidently manipulate fractions, convert between different forms (mixed number, improper fraction, decimal), and choose the most efficient method to solve a problem is a hallmark of strong mathematical proficiency. This isn't just about getting the right answer; it's about developing a deeper understanding of how numbers interact and the underlying logic of mathematical operations.
Conclusion: Mastering Fraction Division
The problem of 8 divided by 1⅓ serves as an excellent illustration of the importance of understanding fraction division. We've explored several different methods for solving this seemingly simple problem, highlighting the underlying mathematical principles and emphasizing the practical applications of such calculations in various fields. By mastering these techniques and fostering a strong understanding of the underlying concepts, you’ll be well-equipped to tackle more complex fraction problems and confidently apply this knowledge in diverse real-world scenarios. Remember, mathematics isn't just about memorizing formulas; it's about developing a deep understanding of how numbers work and the logic behind mathematical operations. This understanding will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Is A Grasshopper A Decomposer
Sep 02, 2025
-
38 Deg C To Fahrenheit
Sep 02, 2025
-
Chlorine 35 Protons Neutrons Electrons
Sep 02, 2025
-
105 Degrees Fahrenheit To Celsius
Sep 02, 2025
-
2x 2 X 1 3
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 8 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.