8 Times What Equals 56
gasmanvison
Sep 10, 2025 · 6 min read
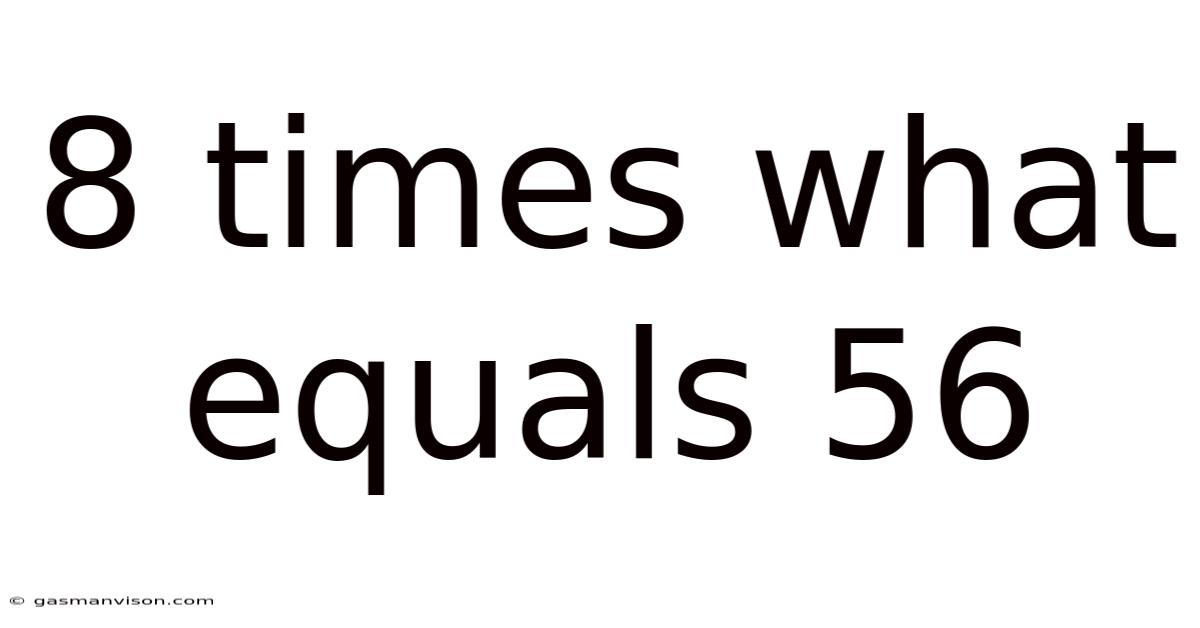
Table of Contents
Unraveling the Mystery: 8 Times What Equals 56? A Deep Dive into Multiplication and Problem Solving
This seemingly simple question, "8 times what equals 56?", opens a door to a world of mathematical concepts, problem-solving strategies, and even practical applications. While the answer itself is straightforward for many, exploring the underlying principles provides a valuable learning opportunity, particularly for those looking to strengthen their foundational mathematical skills or for educators seeking engaging ways to teach multiplication. This article delves deep into this question, exploring various approaches to find the solution, connecting it to broader mathematical concepts, and demonstrating its relevance in real-world scenarios.
Meta Description: Discover the solution to "8 times what equals 56?" and explore the underlying mathematical concepts, problem-solving strategies, and real-world applications of this simple yet insightful question. Learn different approaches to solve similar problems and enhance your mathematical skills.
1. The Direct Approach: Unveiling the Answer
The most direct way to answer "8 times what equals 56?" involves employing the fundamental concept of division. Since multiplication and division are inverse operations, we can find the unknown number by dividing 56 by 8.
8 x ? = 56
? = 56 ÷ 8
? = 7
Therefore, the answer is 7. Eight times seven equals fifty-six (8 x 7 = 56). This simple calculation forms the bedrock of understanding the problem.
2. Visualizing Multiplication: A Pictorial Approach
For those who benefit from visual aids, representing the problem pictorially can significantly improve understanding. Imagine arranging objects into groups of eight. How many groups of eight do you need to reach a total of 56 objects? Visualizing this process helps solidify the concept of multiplication and its inverse, division.
You could draw 7 groups of 8 dots, for example, demonstrating that 7 groups of 8 dots add up to a total of 56 dots. This visual representation reinforces the numerical solution and provides a tangible understanding of the mathematical relationship.
3. Exploring Different Multiplication Strategies
Beyond the simple division approach, several strategies can help solve similar multiplication problems. These strategies are particularly useful when dealing with larger numbers or more complex equations:
-
Repeated Addition: This is a fundamental approach, especially for younger learners. Adding eight seven times (8 + 8 + 8 + 8 + 8 + 8 + 8) yields 56. This method provides a tangible understanding of multiplication as repeated addition.
-
Using Multiplication Tables: Familiarity with multiplication tables provides a quick and efficient way to solve this type of problem. A well-memorized multiplication table instantly reveals that 8 multiplied by 7 equals 56.
-
Factoring: This advanced strategy involves breaking down numbers into their factors. Since 56 can be factored as 8 x 7, the solution becomes immediately apparent. Understanding factoring is crucial for advanced mathematical concepts.
-
Long Division: For larger numbers, long division provides a structured approach to finding the answer. While not necessary for this specific problem, mastering long division is essential for solving more complex mathematical problems.
4. Extending the Concept: Word Problems and Real-World Applications
The question "8 times what equals 56?" is not merely an abstract mathematical exercise. It serves as a foundation for solving real-world problems:
-
Sharing Equally: Imagine you have 56 candies to distribute equally among 8 friends. How many candies does each friend receive? This translates directly to the problem of dividing 56 by 8, leading to the same solution: 7 candies per friend.
-
Calculating Costs: Suppose each pack of pencils costs $8, and you spent $56 in total. How many packs did you buy? This scenario again requires dividing the total cost ($56) by the cost per pack ($8), yielding the answer: 7 packs of pencils.
-
Measuring Distances: If you travel at a constant speed of 8 kilometers per hour and cover a total distance of 56 kilometers, how many hours did it take? This problem translates directly to dividing the total distance (56 km) by the speed (8 km/hour), leading to the solution of 7 hours.
-
Scaling Recipes: Imagine you're baking and a recipe calls for 8 cups of flour to make 56 cookies. How many cups of flour would you need to make 7 cookies (assuming a proportional scaling)? This involves setting up a proportion and solving for the unknown variable, which again connects to the core concept of dividing 56 by 8.
These examples illustrate how the seemingly simple question of "8 times what equals 56?" forms a basis for solving numerous real-world problems, highlighting the practical application of mathematical concepts in everyday life.
5. Connecting to Broader Mathematical Concepts
This simple equation touches upon several important mathematical concepts:
-
Inverse Operations: Understanding that multiplication and division are inverse operations is crucial for solving this and similar problems. This concept forms a fundamental building block of algebra and beyond.
-
Number Properties: The properties of numbers, such as commutativity (the order of numbers in multiplication doesn't change the result), are subtly involved. Whether you calculate 8 x 7 or 7 x 8, the answer remains the same (56).
-
Proportions and Ratios: The problem can be extended to understand proportions and ratios. The ratio of 8 to 56 is equivalent to the ratio of 1 to 7. This concept is essential for solving more complex problems involving scaling, percentages, and other mathematical applications.
-
Algebraic Equations: This simple problem can be expressed as an algebraic equation: 8x = 56, where 'x' represents the unknown number. Solving this equation involves the same process of dividing both sides by 8 to isolate 'x', which demonstrates a foundational understanding for more complex algebraic equations.
6. Problem-Solving Strategies Beyond the Numerical Solution
Beyond finding the numerical answer, the process of solving this problem highlights valuable problem-solving skills:
-
Understanding the Problem: Clearly defining the question and identifying the unknown variable is the first step in effective problem-solving.
-
Choosing the Right Strategy: Selecting the appropriate mathematical approach – division, repeated addition, or other methods – is crucial for efficient problem-solving.
-
Checking the Answer: Verifying the solution through alternative methods or estimations is essential to ensure accuracy. In this case, multiplying 8 by 7 confirms the correctness of the solution.
-
Generalizing the Approach: Learning to adapt the problem-solving approach to similar problems with different numbers is essential for developing proficiency in mathematics. The skills gained in solving "8 times what equals 56?" can be directly applied to solving problems involving other numbers.
7. The Importance of Practice and Repetition
Mastering multiplication and related concepts requires consistent practice. Regular practice with similar problems, involving different numbers and contexts, strengthens mathematical skills and builds confidence. The more exposure you have to these types of problems, the faster and more efficiently you'll be able to solve them. Practice can be incorporated through various means including worksheets, online games, and real-world applications.
8. Conclusion: A Simple Question with Profound Implications
The question "8 times what equals 56?" may seem trivial at first glance. However, a deeper exploration reveals its significance as a foundation for understanding fundamental mathematical concepts, honing problem-solving skills, and applying mathematical knowledge to real-world situations. By understanding the various approaches to solve this problem and its connections to broader mathematical concepts, individuals can significantly enhance their mathematical abilities and develop a stronger foundation for future learning. From simple arithmetic to complex algebraic equations, this seemingly simple question serves as a stepping stone to a deeper appreciation of the power and practicality of mathematics.
Latest Posts
Latest Posts
-
Honest Is To Genuine As
Sep 10, 2025
-
Slider Owns A Hamburger Restaurant
Sep 10, 2025
-
What Time Zone Is La
Sep 10, 2025
-
How Many Inches Is 150mm
Sep 10, 2025
-
Which Sentence Is More Formal
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 8 Times What Equals 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.