90000 Is 1 10 Of
gasmanvison
Sep 20, 2025 · 4 min read
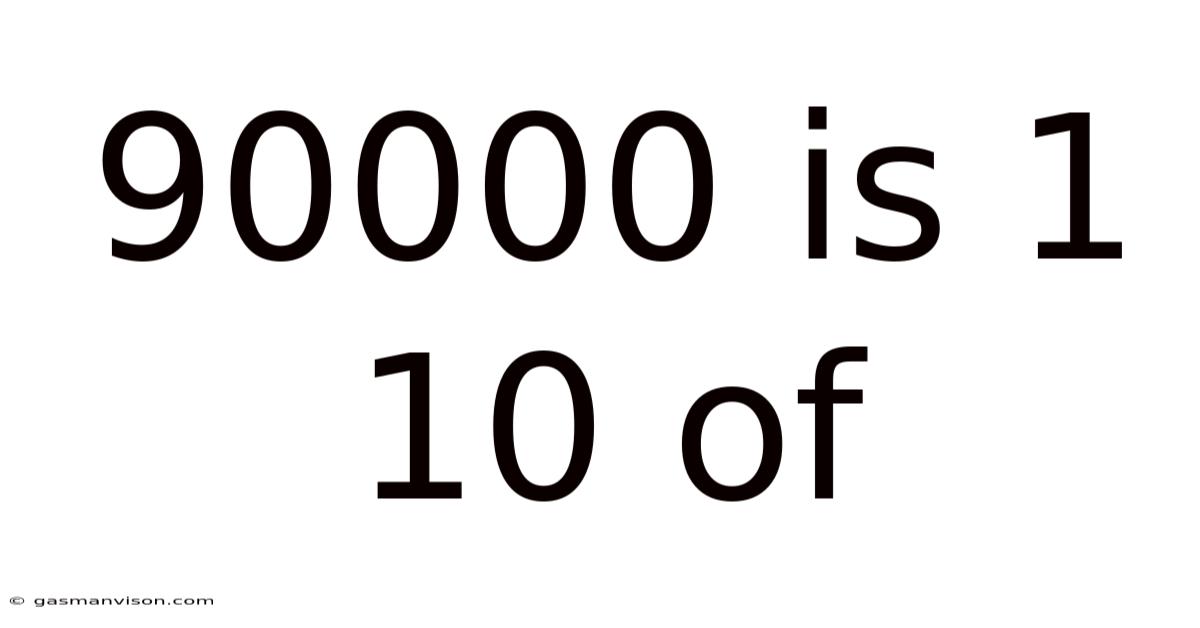
Table of Contents
90,000 is 1/10 of: Solving the Math Problem and Understanding Proportions
This article delves into the seemingly simple question: "90,000 is 1/10 of what number?" While the calculation itself is straightforward, understanding the underlying concepts of fractions, proportions, and their applications in real-world scenarios is crucial. We'll explore the solution, discuss different approaches to solving similar problems, and highlight the importance of proportional reasoning in various fields. This detailed explanation aims to provide a comprehensive understanding, beneficial for students, professionals, and anyone curious about mathematics.
Understanding the Problem: Fractions and Proportions
The core of this problem lies in understanding fractions and proportions. A fraction represents a part of a whole. In this case, 1/10 signifies one-tenth of a larger quantity. A proportion, on the other hand, is a statement of equality between two ratios. We can express the problem as a proportion:
1/10 = 90,000/x
Where 'x' represents the unknown number we're trying to find. This equation states that one-tenth is equivalent to the ratio of 90,000 to the unknown number.
Solving the Equation: Three Methods
We can solve this equation using several methods:
1. Cross-Multiplication: This is a common and straightforward technique for solving proportions. We cross-multiply the terms:
1 * x = 10 * 90,000
This simplifies to:
x = 900,000
Therefore, 90,000 is 1/10 of 900,000.
2. Using the Reciprocal: Since 1/10 represents one-tenth, we can find the whole by multiplying 90,000 by the reciprocal of 1/10, which is 10/1 or simply 10:
90,000 * 10 = 900,000
This method directly utilizes the relationship between a fraction and its whole.
3. Decimal Conversion: We can convert the fraction 1/10 to its decimal equivalent, which is 0.1. The problem then becomes:
0.1 * x = 90,000
Dividing both sides by 0.1 (or multiplying by 10), we get:
x = 900,000
This method demonstrates the interchangeability between fractions and decimals in solving proportions.
Real-World Applications of Proportional Reasoning
Understanding proportions is essential in numerous real-world situations. Here are a few examples:
-
Scaling Recipes: If a recipe calls for 1/2 cup of sugar and you want to double the recipe, you use proportional reasoning to determine the amount of sugar needed (1 cup). Similarly, reducing a recipe involves the same principle.
-
Calculating Percentages: Percentages are essentially fractions with a denominator of 100. Calculating discounts, tax amounts, or interest rates all involve proportional reasoning. For example, finding 15% of a price is equivalent to finding 15/100 of that price.
-
Map Scales: Maps utilize proportions to represent large geographical areas on a smaller scale. The map's scale indicates the ratio between the distance on the map and the actual distance on the ground.
-
Financial Modeling: In finance, proportions are used extensively in areas like budgeting, forecasting, and investment analysis. For example, determining the percentage allocation of investments across different asset classes requires understanding and applying proportional reasoning.
-
Engineering and Construction: Engineers and construction workers use proportions to scale blueprints, calculate material quantities, and ensure structural integrity. Accurate scaling is critical in these fields, often involving complex calculations based on proportional relationships.
-
Scientific Experiments: In scientific experiments, proportions are crucial for accurate measurements, data analysis, and reproducing results. Maintaining consistent ratios of chemicals or adjusting sample sizes requires precise proportional reasoning.
Expanding the Concept: Solving More Complex Proportions
The basic principle of solving proportions remains consistent even with more complex scenarios. Consider this example:
"If 15% of a number is 3000, what is the number?"
We can set up a proportion:
15/100 = 3000/x
Cross-multiplying, we get:
15x = 300,000
x = 20,000
Therefore, 3000 is 15% of 20,000.
Dealing with Different Units:
Proportions can involve different units. For example:
"If a car travels 120 miles in 2 hours, how far will it travel in 5 hours at the same speed?"
We can set up a proportion:
120 miles / 2 hours = x miles / 5 hours
Cross-multiplying and solving for x:
2x = 600
x = 300 miles
Therefore, the car will travel 300 miles in 5 hours. Notice how the units (miles and hours) are maintained consistently throughout the proportion.
Importance of Accuracy and Checking Your Work
When working with proportions, especially in real-world applications, accuracy is paramount. Always double-check your calculations and ensure the units are consistent. A small error in a proportion can lead to significant discrepancies in the results. For instance, in engineering, a slight inaccuracy in a proportion could compromise structural integrity. In finance, a small error could lead to substantial financial losses.
Conclusion: Mastering Proportional Reasoning
The seemingly simple problem of "90,000 is 1/10 of what number?" opens a window into the vast world of proportions and their applications. Understanding proportions is a fundamental mathematical skill with far-reaching implications. From everyday tasks like cooking to complex engineering projects, mastering proportional reasoning is essential for problem-solving and critical thinking in various aspects of life. This article provides a comprehensive overview of how to approach and solve such problems, emphasizing the importance of accuracy, understanding the underlying concepts, and applying these principles to real-world scenarios. By grasping the concepts discussed here, you’ll be well-equipped to tackle more challenging proportional problems and apply this vital skill to various fields.
Latest Posts
Latest Posts
-
What Is Half Of 7 8
Sep 20, 2025
-
Are Trigonal Bipyramidal Molecules Polar
Sep 20, 2025
-
Whats Half Of 2 3 Cup
Sep 20, 2025
-
Is 4 Quarts A Gallon
Sep 20, 2025
-
60 Ml How Many Ounces
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 90000 Is 1 10 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.