Cos X Sin 2x 1
gasmanvison
Sep 14, 2025 · 5 min read
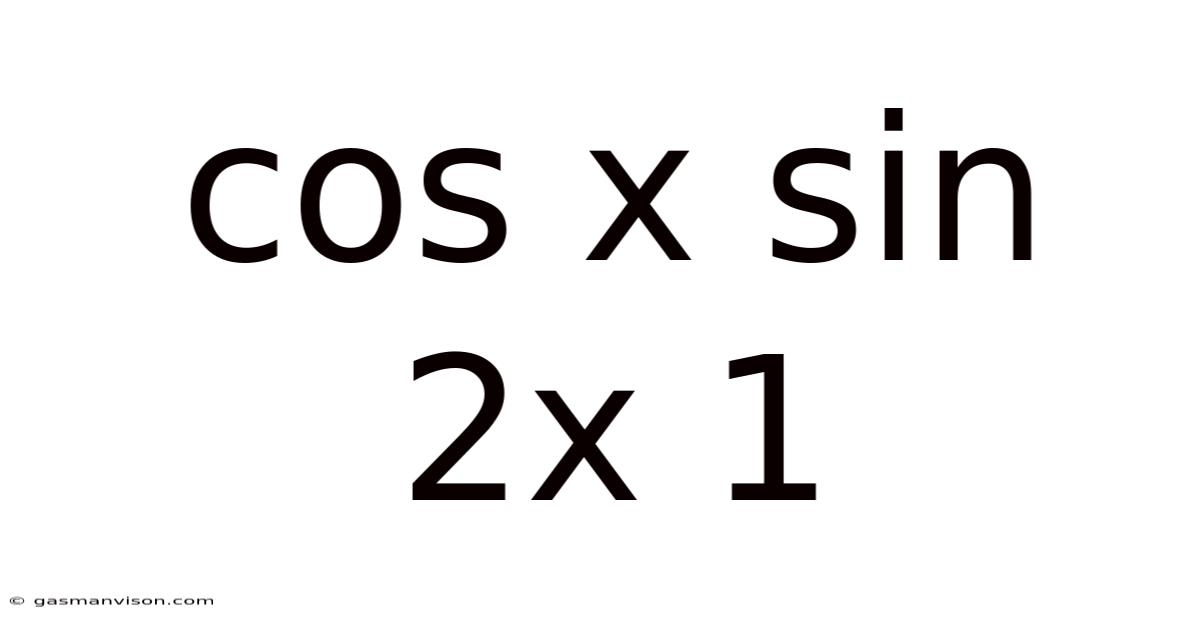
Table of Contents
Exploring the Trigonometric Expression: cos x sin 2x + 1
This article delves into the intricacies of the trigonometric expression cos x sin 2x + 1, exploring its simplification, applications, and potential uses in various mathematical contexts. We'll examine its properties, uncover hidden identities, and discuss strategies for solving equations involving this expression. Understanding this seemingly simple expression reveals a surprising depth of mathematical richness. This exploration will be valuable for students of trigonometry, calculus, and anyone interested in the beauty and power of mathematical identities.
Meta Description: Uncover the hidden depths of the trigonometric expression cos x sin 2x + 1. This comprehensive guide explores its simplification, applications, and solutions to equations involving this intriguing mathematical concept.
1. Simplifying cos x sin 2x + 1 using Trigonometric Identities
The key to understanding and manipulating cos x sin 2x + 1 lies in leveraging fundamental trigonometric identities. The double-angle formula for sine, sin 2x = 2 sin x cos x, provides a crucial starting point. Substituting this identity into our expression, we get:
cos x (2 sin x cos x) + 1
Simplifying further, we obtain:
2 sin x cos²x + 1
This form is already significantly simpler than the original expression, but we can explore further simplifications depending on the context and desired outcome. For example, we can use the Pythagorean identity, sin²x + cos²x = 1, to express cos²x in terms of sin²x:
cos²x = 1 - sin²x
Substituting this into our simplified expression:
2 sin x (1 - sin²x) + 1
This expands to:
2 sin x - 2 sin³x + 1
This final form expresses the original expression entirely in terms of the sine function. The choice of which simplified form to use depends heavily on the specific problem or application. Sometimes, the form 2 sin x cos²x + 1 is more convenient; other times, the expression in terms of sine alone (2 sin x - 2 sin³x + 1) is preferable.
2. Solving Equations Involving cos x sin 2x + 1
Let's consider solving equations where cos x sin 2x + 1 is involved. Suppose we have the equation:
cos x sin 2x + 1 = 0
Using the simplified form 2 sin x cos²x + 1 = 0, we can rearrange the equation:
2 sin x cos²x = -1
This equation is more challenging to solve directly. Numerical methods or graphical techniques might be necessary to find approximate solutions. However, understanding the behavior of the constituent functions – sine and cosine – can help us analyze the possible solutions.
Alternatively, using the form 2 sin x - 2 sin³x + 1 = 0, we have a cubic equation in sin x. Solving cubic equations can be complex, often requiring the use of the cubic formula or numerical methods.
Let's consider a slightly different equation:
cos x sin 2x + 1 = k, where k is a constant.
The solutions to this equation will depend heavily on the value of k. For instance, if k=1, then cos x sin 2x = 0, which implies either cos x = 0 or sin 2x = 0. This leads to specific solutions for x. Different values of k will yield different solution sets.
3. Graphical Representation and Analysis
Visualizing the function f(x) = cos x sin 2x + 1 graphically provides valuable insights into its behavior. Plotting this function reveals its periodic nature and identifies key features like maxima, minima, and zeros. The graph helps illustrate the range of possible values and the intervals where the function is positive or negative. This visual representation aids in understanding the solutions to equations involving this expression. Software like Desmos or GeoGebra can be used to generate such graphs. Observing the graph allows for a better understanding of the function's periodicity and the distribution of its zeros and extrema, ultimately leading to more efficient problem solving.
4. Applications in Calculus and Differential Equations
The expression cos x sin 2x + 1 can appear in various calculus problems, such as:
-
Differentiation: Finding the derivative of this expression involves applying the chain rule and product rule. The derivative would be useful in optimization problems or in determining the rate of change of the function.
-
Integration: Integrating this expression might require techniques like integration by parts or trigonometric substitution. The integral would represent the area under the curve of the function.
-
Differential Equations: This expression could appear in differential equations, requiring techniques like separation of variables or integrating factors to find solutions.
5. Relationship to Other Trigonometric Identities
The expression cos x sin 2x + 1 is closely related to several other trigonometric identities. Its simplification relies heavily on the double-angle formula for sine and the Pythagorean identity. Understanding its connection to these fundamental identities allows for a more profound understanding of its behavior and potential transformations. Exploring these connections reveals a network of interconnected trigonometric relationships. This interconnectedness highlights the elegance and internal consistency of trigonometry.
6. Advanced Applications and Further Exploration
Beyond the fundamental applications discussed, cos x sin 2x + 1 could appear in more advanced mathematical contexts:
-
Fourier Analysis: This expression might emerge in the context of Fourier series or transforms, particularly when dealing with periodic functions.
-
Signal Processing: In signal processing, trigonometric expressions like this one often represent signals or waveforms, and their analysis is crucial for signal manipulation and understanding.
-
Physics: Many physical phenomena are modeled using trigonometric functions, and this expression could appear in modeling oscillations, waves, or other periodic processes.
7. Conclusion
The trigonometric expression cos x sin 2x + 1, although seemingly simple, reveals a significant depth of mathematical richness. Through simplification using fundamental trigonometric identities, we can transform it into more manageable forms, facilitating equation solving and analysis. Its graphical representation offers valuable insights into its behavior. Furthermore, its applications extend to various areas like calculus, differential equations, and potentially more advanced mathematical fields. A thorough understanding of this expression strengthens one's grasp of trigonometry and its far-reaching applications. Further exploration into its properties and applications could lead to discoveries and insights in various scientific and mathematical domains. The simplicity of the expression belies its power and potential within a wide range of mathematical and scientific contexts. Its adaptability and connections to other fundamental trigonometric identities solidify its significance in mathematical study.
Latest Posts
Latest Posts
-
How To Start A Summary
Sep 14, 2025
-
A Company Manufactures Two Products
Sep 14, 2025
-
Factors Of 80 In Pairs
Sep 14, 2025
-
What Is 14kg In Lbs
Sep 14, 2025
-
Baking Soda Vinegar Reaction Equation
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Cos X Sin 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.