Cos2x Cos 2x Sin 2x
gasmanvison
Sep 06, 2025 · 5 min read
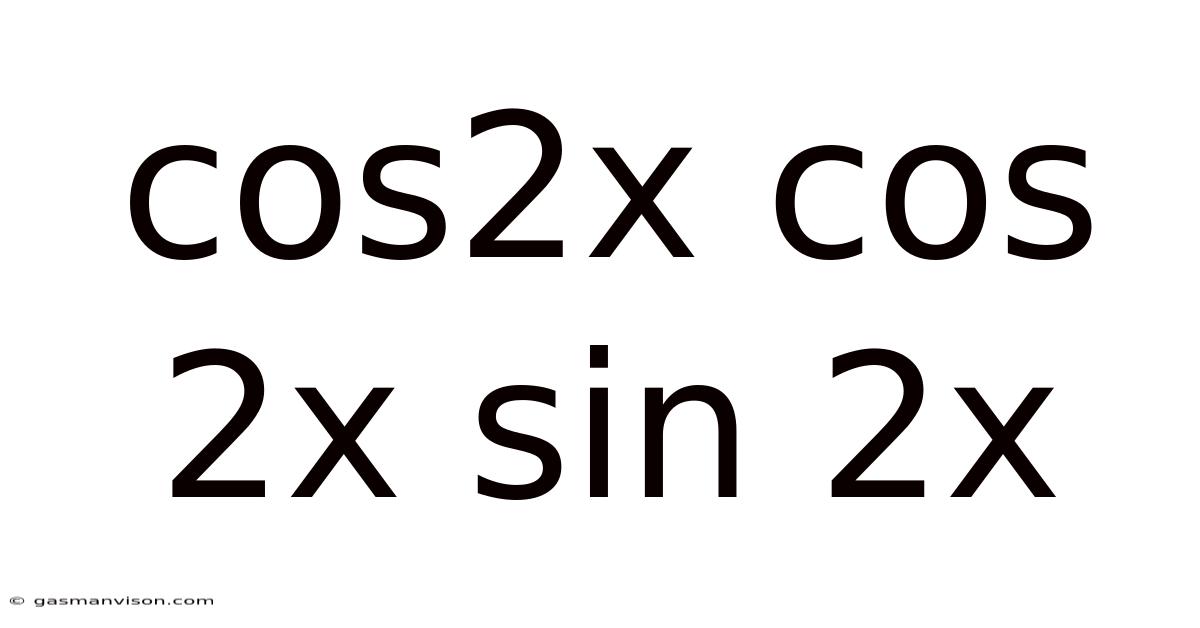
Table of Contents
Decoding the Trigonometric Expression: cos²2x + cos2x sin2x
This article delves deep into the trigonometric expression cos²2x + cos2x sin2x, exploring its simplification, applications, and connections to other trigonometric identities. We'll uncover its hidden properties and demonstrate its practical use in various mathematical contexts. Understanding this expression unlocks a deeper appreciation for the interconnectedness of trigonometric functions and their power in solving complex problems. This comprehensive guide will equip you with the knowledge and tools to confidently tackle similar expressions and expand your understanding of trigonometry.
Meta Description: Explore the intricacies of the trigonometric expression cos²2x + cos2x sin2x. This comprehensive guide simplifies the expression, reveals its applications, and connects it to other trigonometric identities, enhancing your understanding of trigonometry.
Understanding the Components: cos2x and sin2x
Before we embark on simplifying cos²2x + cos2x sin2x, let's refresh our understanding of the double angle formulas for cosine and sine. These are fundamental building blocks for working with this expression.
-
cos2x: The double angle formula for cosine offers several equivalent expressions:
- cos2x = cos²x - sin²x
- cos2x = 2cos²x - 1
- cos2x = 1 - 2sin²x
-
sin2x: Similarly, the double angle formula for sine is:
- sin2x = 2sinx cosx
These alternative forms are crucial, as they allow us to manipulate the expression cos²2x + cos2x sin2x in different ways, potentially leading to simpler forms depending on the context of the problem.
Simplifying cos²2x + cos2x sin2x: Multiple Approaches
The simplification of cos²2x + cos2x sin2x isn't immediately obvious. However, several strategic approaches can lead to a more manageable expression. Let's explore some key methods:
Method 1: Factoring out cos2x
The most straightforward approach involves factoring out the common term cos2x:
cos²2x + cos2x sin2x = cos2x (cos2x + sin2x)
This simplification is elegant and efficient. Notice that (cos2x + sin2x) is a crucial part. Recall the Pythagorean identity: cos²θ + sin²θ = 1. While we have 2x instead of θ, the identity still holds true. Therefore:
cos2x + sin2x = 1
Substituting this back into our factored expression, we get a remarkably simplified result:
cos²2x + cos2x sin2x = cos2x (1) = cos2x
This highlights the power of recognizing and applying fundamental trigonometric identities. The seemingly complex expression simplifies to a single term – cos2x.
Method 2: Expanding using Double Angle Formulas
Alternatively, we can expand the expression using the different forms of the double angle formulas for cos2x and sin2x. This approach demonstrates a different pathway to the same simplified result, solidifying our understanding. Let's explore this method:
Starting with cos²2x + cos2x sin2x, we can replace cos2x with (2cos²x - 1) and sin2x with (2sinxcosx):
(2cos²x - 1)² + (2cos²x - 1)(2sinxcosx)
Expanding this expression will lead to a more complex intermediate step. However, through careful simplification and application of trigonometric identities (like the Pythagorean identity), you'll eventually arrive at the same simplified form: cos2x. This method, while more involved, reinforces the interconnectedness of trigonometric identities and the multiple pathways to simplifying expressions.
Method 3: Using Sum-to-Product Formulas (A More Advanced Approach)
For a more advanced approach, we can leverage sum-to-product formulas. While this method is not the most efficient for this specific expression, it demonstrates the versatility of trigonometric identities. The sum-to-product formulas allow us to express sums of trigonometric functions as products. While not directly applicable for this particular simplification in the most straightforward manner, understanding these formulas is crucial for tackling more complex trigonometric expressions.
Applications of cos2x
Now that we've simplified our original expression to cos2x, let's explore the applications of this fundamental trigonometric function. cos2x appears frequently in various fields, including:
-
Physics: Describing oscillatory motion, such as the motion of a pendulum or a spring-mass system. The function models the displacement or velocity of the object as a function of time.
-
Engineering: Analyzing alternating current (AC) circuits. The cosine function is crucial in representing the sinusoidal voltage and current waveforms.
-
Computer Graphics: Used in creating smooth curves and animations, particularly in 2D and 3D graphics.
-
Signal Processing: Analyzing and manipulating signals with periodic components. The cosine function forms the basis for Fourier analysis, a powerful technique for decomposing complex signals into simpler sinusoidal components.
-
Calculus: cos2x plays a vital role in integration and differentiation problems, often appearing in problems involving trigonometric substitution or integration by parts.
Further Exploration and Related Identities
Understanding cos²2x + cos2x sin2x provides a stepping stone to tackling more intricate trigonometric expressions. Here are some related identities and concepts for further exploration:
-
Triple Angle Formulas: These formulas express trigonometric functions of 3θ in terms of functions of θ. They build upon the double angle formulas and often involve similar simplification techniques.
-
Half Angle Formulas: These formulas express trigonometric functions of θ/2 in terms of functions of θ. They are useful in solving equations or simplifying expressions involving half angles.
-
Product-to-Sum Formulas: These identities express products of trigonometric functions as sums or differences of trigonometric functions. They are often helpful in simplifying expressions involving products of sine and cosine terms.
-
Power-Reducing Formulas: These formulas allow you to express higher powers of trigonometric functions (like cos⁴x or sin³x) as lower powers, simplifying calculations and integration processes.
Conclusion: Mastering Trigonometric Simplification
Simplifying trigonometric expressions like cos²2x + cos2x sin2x requires a strong foundation in trigonometric identities and a strategic approach to problem-solving. By understanding the double angle formulas, Pythagorean identity, and applying factoring techniques, we efficiently simplified the given expression to cos2x. This journey highlights the importance of recognizing and applying fundamental trigonometric identities, fostering a deeper understanding of the interconnectedness within trigonometry. This skill translates directly to more complex problems in calculus, physics, engineering, and other fields where trigonometric functions play a significant role. Mastering these techniques empowers you to approach complex problems with confidence and efficiency. Continuous practice and exploration of related identities will further enhance your skills and deepen your understanding of the elegance and power of trigonometry.
Latest Posts
Latest Posts
-
Lewis Dot Structure For Seo2
Sep 06, 2025
-
Is 20 A Perfect Square
Sep 06, 2025
-
2 Types Of Behavioral Adaptations
Sep 06, 2025
-
How To Compute Percent Yield
Sep 06, 2025
-
Para Comer Una Ensalada Necesitas
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about Cos2x Cos 2x Sin 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.