Factor 2x 2 7x 3
gasmanvison
Sep 10, 2025 · 6 min read
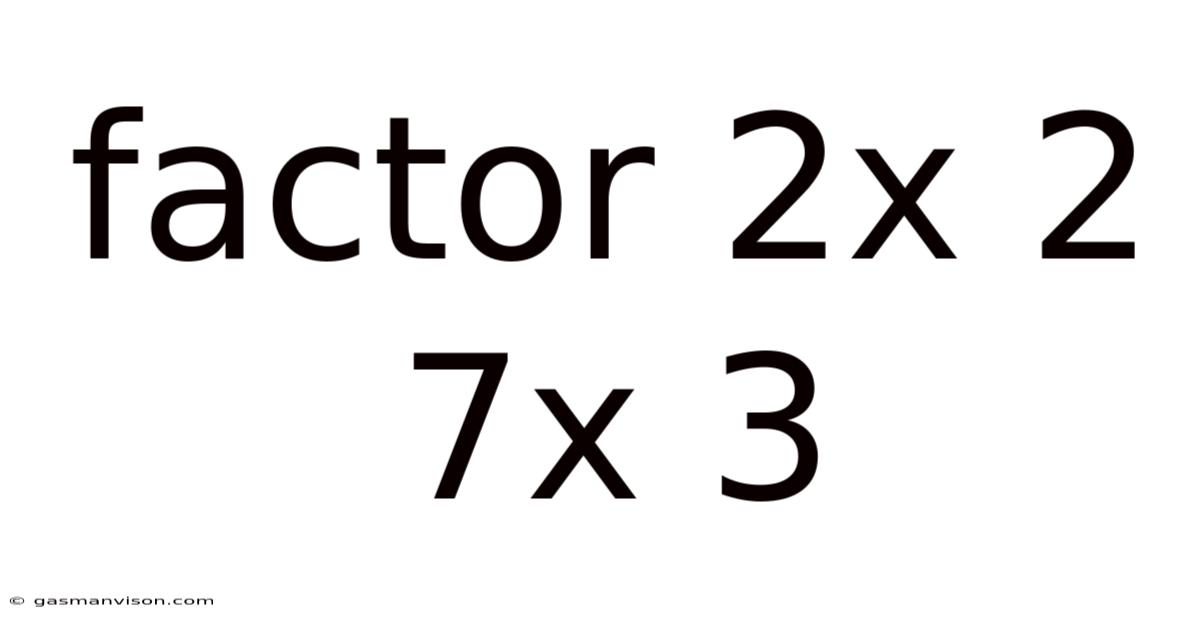
Table of Contents
Decomposing and Solving Quadratic Expressions: A Deep Dive into 2x² + 7x + 3
This article delves into the intricacies of factoring the quadratic expression 2x² + 7x + 3, exploring various methods and providing a comprehensive understanding of the underlying mathematical principles. We'll move beyond simply finding the factors and explore the broader context of quadratic equations, their applications, and the significance of factoring in solving them. This guide is designed for students seeking a deeper understanding of algebra, as well as anyone interested in strengthening their mathematical problem-solving skills.
What is Factoring?
Before diving into the specifics of factoring 2x² + 7x + 3, let's establish a foundational understanding. Factoring, in the context of algebra, is the process of expressing a mathematical expression as a product of simpler expressions. This is essentially the reverse of expanding (or multiplying out) expressions. For example, expanding (x + 2)(x + 3) gives us x² + 5x + 6. Factoring x² + 5x + 6 would then reverse this process, leading us back to (x + 2)(x + 3).
Why is Factoring Important?
Factoring quadratic expressions like 2x² + 7x + 3 is a crucial skill in algebra for several reasons:
-
Solving Quadratic Equations: Many quadratic equations can be solved efficiently by factoring. Setting the factored expression equal to zero allows us to use the zero-product property, which states that if the product of two factors is zero, then at least one of the factors must be zero. This simplifies the process of finding the roots (or solutions) of the equation.
-
Simplifying Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and understand. This is particularly useful in calculus and other advanced mathematical fields.
-
Understanding the Structure of Polynomials: Factoring helps us understand the structure and behavior of polynomials. It reveals the roots of the polynomial and provides insights into its graph.
-
Applications in Real-World Problems: Quadratic equations and their solutions are used to model various real-world phenomena, including projectile motion, area calculations, and optimization problems. The ability to factor these equations is essential for solving these problems.
Methods for Factoring 2x² + 7x + 3
There are several methods to factor 2x² + 7x + 3. We will explore two common approaches:
1. The AC Method:
This method is particularly useful for factoring quadratic expressions of the form ax² + bx + c, where a ≠ 1 (as in our case, where a = 2). The steps are as follows:
-
Find the product AC: In our case, a = 2 and c = 3, so AC = 2 * 3 = 6.
-
Find two numbers that add up to B and multiply to AC: We need two numbers that add up to 7 (our b value) and multiply to 6. These numbers are 1 and 6.
-
Rewrite the middle term: Rewrite the middle term (7x) as the sum of the two numbers found in the previous step: 1x and 6x. Our expression becomes 2x² + 1x + 6x + 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x(2x + 1) + 3(2x + 1)
-
Factor out the common binomial factor: Notice that (2x + 1) is a common factor in both terms. Factor it out:
(2x + 1)(x + 3)
Therefore, the factored form of 2x² + 7x + 3 is (2x + 1)(x + 3).
2. Trial and Error:
This method involves systematically trying different combinations of binomial factors until you find the correct one. It's often faster for simpler quadratic expressions.
Since the coefficient of x² is 2, the factors will likely involve 2x and x. The constant term is 3, so the factors of 3 are 1 and 3. We need to arrange these factors to get the correct middle term, 7x.
Let's try (2x + 1)(x + 3):
Expanding this gives us 2x² + 6x + x + 3 = 2x² + 7x + 3. This matches our original expression, so (2x + 1)(x + 3) is the correct factorization.
Solving the Quadratic Equation 2x² + 7x + 3 = 0
Now that we've factored the expression, we can solve the corresponding quadratic equation:
2x² + 7x + 3 = 0
(2x + 1)(x + 3) = 0
Using the zero-product property, we set each factor equal to zero and solve for x:
2x + 1 = 0 => 2x = -1 => x = -1/2
x + 3 = 0 => x = -3
Therefore, the solutions to the quadratic equation 2x² + 7x + 3 = 0 are x = -1/2 and x = -3.
Understanding the Graph of the Quadratic Function
The quadratic function y = 2x² + 7x + 3 represents a parabola. The solutions we found (-1/2 and -3) represent the x-intercepts of this parabola – the points where the parabola crosses the x-axis. The parabola opens upwards because the coefficient of x² (2) is positive. The vertex of the parabola (the lowest point) can be found using the formula x = -b / 2a, where a = 2 and b = 7. This gives us x = -7/4. Substituting this value back into the equation gives us the y-coordinate of the vertex.
Further Exploration: More Complex Quadratic Expressions
While this article focused on factoring 2x² + 7x + 3, the principles discussed apply to more complex quadratic expressions. Expressions with larger coefficients or those involving irrational or complex roots may require more sophisticated techniques, such as the quadratic formula or completing the square. However, mastering the fundamental techniques presented here provides a solid foundation for tackling these more challenging problems. Understanding the relationship between factoring, solving quadratic equations, and graphing parabolas is crucial for success in algebra and beyond.
Applications in Real-World Scenarios
The ability to factor quadratic expressions isn't just a theoretical exercise; it has practical applications in various fields:
-
Physics: Projectile motion is often modeled using quadratic equations. Factoring these equations helps determine the time it takes for a projectile to reach its maximum height or hit the ground.
-
Engineering: Engineers use quadratic equations to design structures, calculate stresses, and optimize designs. Factoring is crucial in solving these equations and making informed decisions.
-
Economics: Quadratic functions can model cost, revenue, and profit functions. Factoring these functions can help businesses determine the break-even point or maximize profits.
-
Computer Science: Quadratic equations and their solutions are used in algorithms and computer graphics.
Conclusion:
Factoring the quadratic expression 2x² + 7x + 3, while seemingly a simple algebraic task, provides a gateway to understanding the deeper concepts of quadratic equations, their solutions, and their various applications. By mastering the techniques presented in this article – the AC method and trial and error – you equip yourself not only with the ability to solve quadratic equations efficiently but also with a deeper appreciation for the elegance and practicality of algebra in real-world problems. Remember that practice is key. The more you work with factoring quadratic expressions, the more proficient and confident you will become. This understanding will serve as a strong foundation for more advanced mathematical concepts in the future.
Latest Posts
Latest Posts
-
Is Hexane Polar Or Nonpolar
Sep 10, 2025
-
Un Automovilista Debe Saber Que
Sep 10, 2025
-
Square Root Of 20 Simplified
Sep 10, 2025
-
Honest Is To Genuine As
Sep 10, 2025
-
Slider Owns A Hamburger Restaurant
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 7x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.