Factor 2x 2 X 15
gasmanvison
Sep 21, 2025 · 6 min read
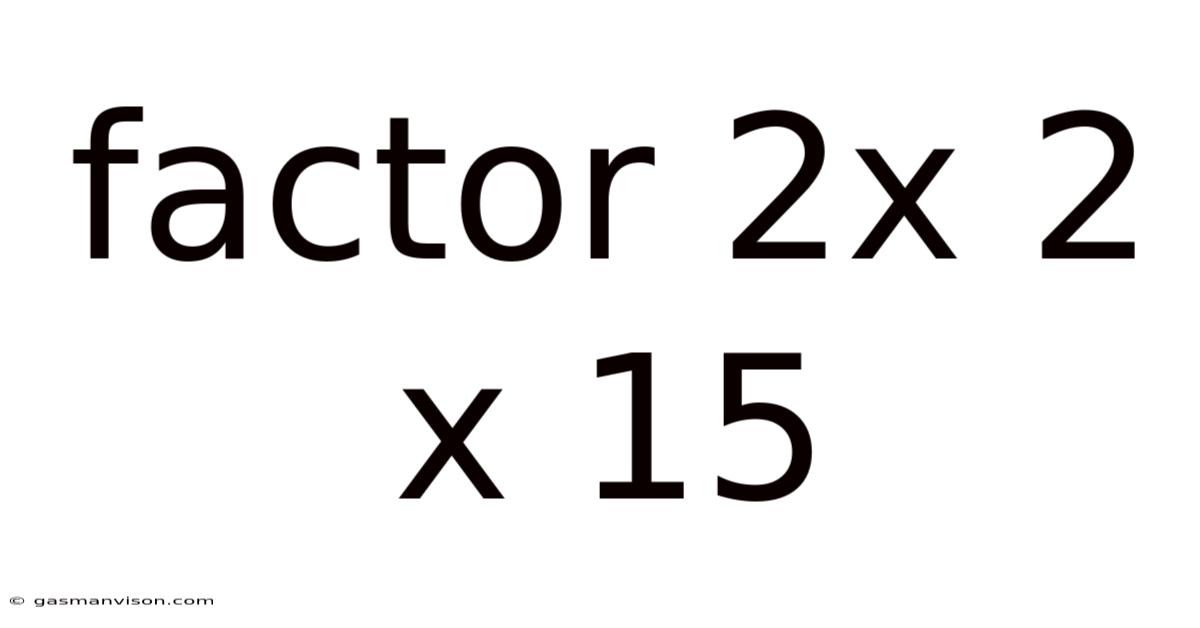
Table of Contents
Decomposing 2 x 2 x 15: A Deep Dive into Prime Factorization and its Applications
This article delves into the seemingly simple mathematical problem of factoring 2 x 2 x 15. While the initial calculation might seem trivial, exploring this problem opens doors to understanding fundamental concepts in number theory, particularly prime factorization, and its wide-ranging applications in various fields. We'll explore the process, the significance of prime numbers, and how this seemingly simple calculation connects to more complex mathematical and computational tasks.
Meta Description: Learn the fundamentals of prime factorization by exploring the decomposition of 2 x 2 x 15. This article details the process, explains the significance of prime numbers, and shows real-world applications of this concept in cryptography and computer science.
Understanding Prime Factorization
Prime factorization is the process of finding the prime numbers that, when multiplied together, equal a given number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This uniqueness is crucial in various mathematical applications.
In our example, 2 x 2 x 15, we are already presented with a factorization, but it’s not a prime factorization because 15 is not a prime number. To find the prime factorization, we need to break down all composite numbers (numbers that are not prime) into their prime components.
Factoring 2 x 2 x 15 into Prime Factors
Let's break down the calculation step-by-step:
-
Identify Composite Numbers: We identify 15 as a composite number.
-
Prime Factorization of 15: We find the prime factors of 15. 15 is divisible by 3 and 5 (both prime numbers). Therefore, 15 = 3 x 5.
-
Complete Prime Factorization: Substituting this back into our original expression, we get: 2 x 2 x 3 x 5.
Therefore, the prime factorization of 2 x 2 x 15 is 2² x 3 x 5. This representation is unique; no other combination of prime numbers will multiply to give the same result.
The Significance of Prime Numbers in Factorization
The concept of prime factorization, as illustrated with our example, is fundamental to number theory. Prime numbers are the building blocks of all integers, and their unique decomposition is the cornerstone of many mathematical algorithms. The difficulty in factoring large numbers into their prime components is the basis of several crucial modern cryptographic systems.
Applications of Prime Factorization
The seemingly simple process of finding the prime factors of a number has far-reaching implications across several fields:
1. Cryptography:
-
RSA Encryption: The RSA algorithm, widely used to secure online transactions, relies heavily on the difficulty of factoring extremely large numbers into their prime components. The public key consists of the product of two large prime numbers, while the private key is derived from these prime factors. The computational effort required to factor these large numbers makes breaking RSA encryption practically infeasible with current computing power. Understanding prime factorization is key to grasping the security of online banking, e-commerce, and secure communication protocols.
-
Other Cryptographic Systems: Many other cryptographic systems, both symmetric and asymmetric, utilize prime numbers and their properties in their design and implementation. The security of these systems directly depends on the computational difficulty of related number-theoretic problems.
2. Computer Science:
-
Algorithm Design: Prime factorization and related concepts are fundamental to many algorithms in computer science, particularly in areas like cryptography, data structures, and algorithm analysis. The efficiency and complexity of these algorithms are often analyzed in terms of their dependence on the size of the input numbers and the prime factorization process.
-
Hashing and Data Structures: Prime numbers are frequently used in hashing algorithms to minimize collisions and improve the efficiency of data structures like hash tables. The selection of prime numbers for hash table sizes often contributes to better performance and reduced search times.
3. Mathematics:
-
Number Theory: Prime factorization is a core concept in number theory. It's used to prove theorems, develop new algorithms, and explore the properties of numbers. The distribution of prime numbers, their density, and related concepts are active areas of research in mathematics.
-
Abstract Algebra: Prime numbers and their properties play a significant role in abstract algebra, particularly in ring theory and field theory. Prime ideals and related concepts are fundamental to these fields.
4. Coding Theory:
- Error Correction: Prime numbers are sometimes used in coding theory for constructing error-correcting codes. These codes help to detect and correct errors that might occur during data transmission or storage. The properties of prime numbers can be leveraged to design efficient and robust error-correcting schemes.
Advanced Concepts Related to Prime Factorization
While 2 x 2 x 15 is a relatively simple example, the complexities surrounding prime factorization grow rapidly with larger numbers. Let's briefly touch upon some more advanced concepts:
-
Trial Division: This is a simple but inefficient method for finding prime factors, particularly for large numbers. It involves testing divisibility by successive prime numbers. While effective for smaller numbers, its computational cost grows exponentially with the size of the number.
-
Sieve of Eratosthenes: This is a more efficient algorithm for finding all prime numbers up to a specified limit. It's a classic algorithm in number theory, and while not directly a prime factorization algorithm, it's a valuable tool in many prime-related computations.
-
Pollard's Rho Algorithm: This is a probabilistic algorithm for factoring integers. It's more efficient than trial division for larger numbers but doesn't guarantee finding all factors.
-
General Number Field Sieve (GNFS): This is currently the most efficient known algorithm for factoring extremely large integers. It's a sophisticated algorithm used to factor numbers with hundreds of digits, essential for breaking some cryptographic systems. However, even GNFS has its computational limits, which makes large prime number-based cryptography secure.
-
The Riemann Hypothesis: This is one of the most important unsolved problems in mathematics. It's related to the distribution of prime numbers and has profound implications for number theory and other mathematical fields. Understanding the distribution of primes is crucial for estimating the difficulty of factoring large numbers.
Conclusion
The seemingly simple problem of factoring 2 x 2 x 15 serves as a gateway to a vast and intricate world of number theory and its applications. While the prime factorization (2² x 3 x 5) is easily obtained in this case, the underlying principles and associated algorithms have profound implications in cryptography, computer science, and various areas of mathematics. Understanding prime factorization is not just about solving simple arithmetic problems; it's about grasping the fundamental building blocks of numbers and their crucial role in securing our digital world and advancing computational frontiers. The seemingly simple act of decomposing a number into its prime factors highlights the power and elegance of mathematical concepts and their surprising relevance in our modern technological landscape. Further exploration into these topics will reveal even greater depth and complexity within the world of numbers.
Latest Posts
Latest Posts
-
What Color Is Opposite Pink
Sep 21, 2025
-
Inverter Sizing Is Based On
Sep 21, 2025
-
A Great Business Idea Is
Sep 21, 2025
-
Food That Is Honestly Presented
Sep 21, 2025
-
Model 4 Period 3 Elements
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 X 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.