Factor 4x 2 X 5
gasmanvison
Sep 16, 2025 · 6 min read
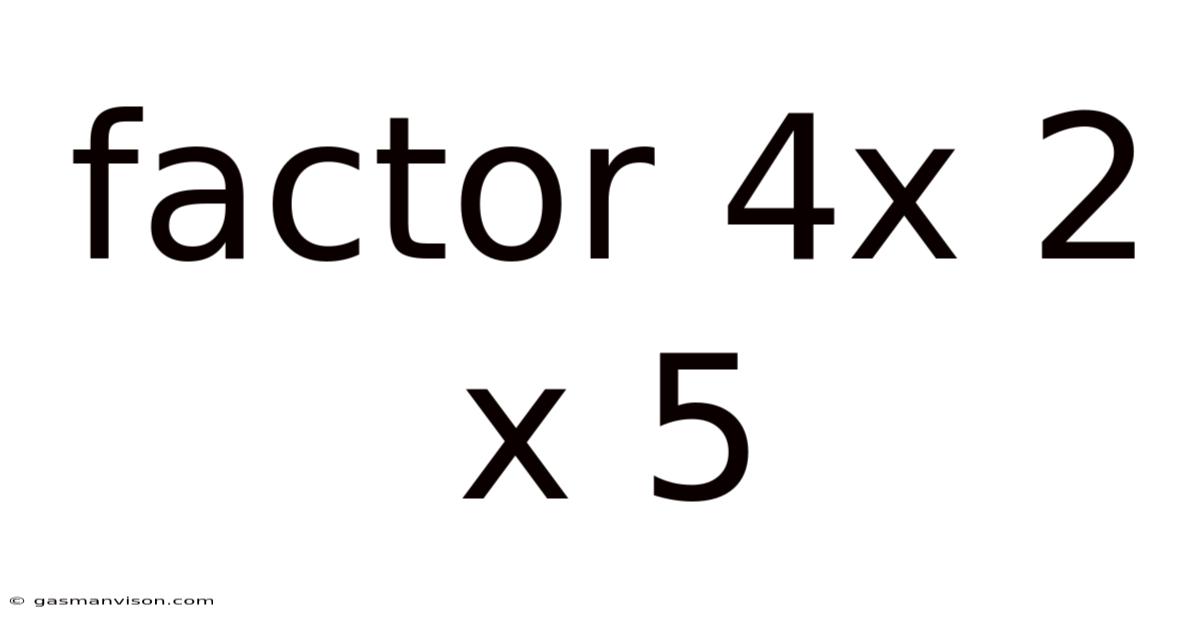
Table of Contents
Decomposing the Multiplication: A Deep Dive into 4 x 2 x 5
This seemingly simple multiplication problem, 4 x 2 x 5, offers a surprisingly rich opportunity to explore fundamental mathematical concepts, delve into various solution strategies, and connect the problem to broader mathematical ideas. This article will dissect this equation, examining its solution from multiple perspectives and highlighting its relevance to different mathematical fields, including arithmetic, algebra, and even number theory. We'll also consider the pedagogical implications of understanding such problems, particularly for young learners.
Meta Description: This article provides a comprehensive exploration of the simple multiplication problem 4 x 2 x 5, examining various solution strategies, connecting it to broader mathematical concepts, and discussing its pedagogical implications for teaching multiplication to young learners.
Understanding the Fundamentals: The Commutative and Associative Properties
Before diving into the various ways to solve 4 x 2 x 5, let's establish the foundational properties that govern multiplication. The commutative property states that the order of the numbers being multiplied does not affect the product. In other words, 4 x 2 x 5 = 2 x 4 x 5 = 5 x 2 x 4, and so on. This flexibility allows us to rearrange the numbers to simplify the calculation.
The associative property dictates that the grouping of numbers during multiplication doesn't alter the outcome. This means (4 x 2) x 5 = 4 x (2 x 5). We can group the numbers in different ways without changing the final answer. These two properties are crucial for efficiently solving multiplication problems, particularly those involving more than two numbers.
Method 1: Sequential Multiplication
The most straightforward approach is to perform the multiplication sequentially. We start with the first two numbers:
4 x 2 = 8
Then, we multiply the result by the remaining number:
8 x 5 = 40
Therefore, 4 x 2 x 5 = 40. This method is simple and easily understood, particularly for beginners learning multiplication. It reinforces the concept of sequential operations.
Method 2: Utilizing the Commutative Property for Easier Calculation
The commutative property allows us to rearrange the numbers to our advantage. Notice that 2 and 5 multiply to 10, a number that's often easier to work with. So, we can rewrite the equation as:
4 x (2 x 5) = 4 x 10 = 40
This approach simplifies the calculation by exploiting the fact that multiplying by 10 is generally simpler than multiplying by other numbers. This strategy highlights the importance of recognizing opportunities for simplification within a mathematical problem.
Method 3: Applying the Associative Property for Simplification
Similar to the previous method, the associative property allows us to group the numbers differently. We can group 4 and 2 first:
(4 x 2) x 5 = 8 x 5 = 40
Or we can group 2 and 5 first:
4 x (2 x 5) = 4 x 10 = 40
Both groupings lead to the same result, demonstrating the power of the associative property in streamlining calculations. This method emphasizes the flexibility offered by the order of operations in multiplication.
Method 4: Visual Representation using Arrays
Multiplication can be visually represented using arrays. Imagine a rectangle with 4 rows and 2 columns. Each cell represents a unit. The total number of cells is 4 x 2 = 8. Now imagine extending this rectangle to have 5 such layers. The total number of cells would be 8 x 5 = 40. This method provides a concrete visual representation of the multiplication process, making it easier for visual learners to grasp the concept. It bridges the gap between abstract mathematical operations and real-world representations.
Method 5: Breaking Down Numbers – Prime Factorization
This method involves breaking down each number into its prime factors. The prime factorization of 4 is 2 x 2, the prime factorization of 2 is simply 2, and the prime factorization of 5 is 5. Therefore, we can rewrite the equation as:
(2 x 2) x 2 x 5 = 2 x 2 x 2 x 5 = 40
This method showcases the fundamental building blocks of numbers and demonstrates how the multiplicative properties are inherent in the prime factorization of numbers. Understanding prime factorization is crucial for numerous advanced mathematical concepts.
Connecting to Larger Concepts: Factors, Multiples, and Divisibility
The equation 4 x 2 x 5 = 40 also provides an excellent opportunity to introduce related concepts:
-
Factors: 4, 2, 5, and 10 are all factors of 40 because they divide evenly into 40. Understanding factors helps in simplifying fractions and solving various mathematical problems.
-
Multiples: 40 is a multiple of 4, 2, 5, 8, 10, and 20. This concept is critical for understanding number patterns and relationships.
-
Divisibility Rules: We can use divisibility rules to determine if a number is divisible by another number. For instance, 40 is divisible by 2 because it's an even number; it's divisible by 5 because it ends in 0; and it's divisible by 10 for the same reason.
These connections enrich the understanding of the initial multiplication problem, placing it within a larger mathematical framework.
Pedagogical Implications: Teaching Multiplication Effectively
The simple equation 4 x 2 x 5 presents a valuable opportunity for teaching multiplication to young learners. The various solution methods discussed above can be tailored to different learning styles:
-
Visual learners: Using arrays and other visual aids.
-
Kinesthetic learners: Using manipulative objects to represent the numbers.
-
Auditory learners: Verbal explanations and discussions.
By introducing multiple methods and connecting the concept to related mathematical ideas, educators can create a more engaging and comprehensive learning experience. This approach fosters a deeper understanding of multiplication beyond simple rote memorization. The ability to choose the most efficient method based on the numbers involved also cultivates problem-solving skills.
Expanding the Horizons: Extending the Concept to Algebra
The principle of multiplication demonstrated in 4 x 2 x 5 readily translates into algebraic concepts. We can represent the numbers using variables:
a x b x c = d
Where a, b, and c represent the numbers 4, 2, and 5 respectively, and d represents the product, 40. This simple substitution introduces the idea of representing numerical relationships symbolically, laying a foundation for understanding algebraic equations and variables.
Further, we can explore the concept of unknowns. For instance:
4 x 2 x x = 40
Solving for 'x' involves applying the reverse operation of multiplication – division. This helps to introduce inverse operations and the concept of solving for unknowns. This bridges the gap between arithmetic and algebra, showcasing the interconnectedness of mathematical concepts.
Conclusion: The Significance of a Simple Problem
The seemingly simple equation 4 x 2 x 5 serves as a microcosm of mathematical principles. Its solution, while straightforward, offers multiple approaches that reveal deeper insights into fundamental mathematical properties such as the commutative and associative properties. By analyzing this problem from various angles, we enhance our understanding not only of multiplication but also of broader mathematical concepts, including prime factorization, factors, multiples, divisibility, and the foundations of algebra. Furthermore, understanding the different pedagogical approaches to teaching this problem highlights the importance of catering to diverse learning styles and building a solid foundation in mathematical reasoning. The seemingly simple 4 x 2 x 5, therefore, proves to be a surprisingly rich and rewarding area of exploration for both students and educators.
Latest Posts
Latest Posts
-
What Is 22kg In Pounds
Sep 16, 2025
-
In Georgia Drivers Must Leav
Sep 16, 2025
-
Is Oh A Strong Base
Sep 16, 2025
-
Height 65 Inches In Feet
Sep 16, 2025
-
13 Times 13 Times 13
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor 4x 2 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.