Factor Completely. Y2 6y 8
gasmanvison
Sep 24, 2025 · 5 min read
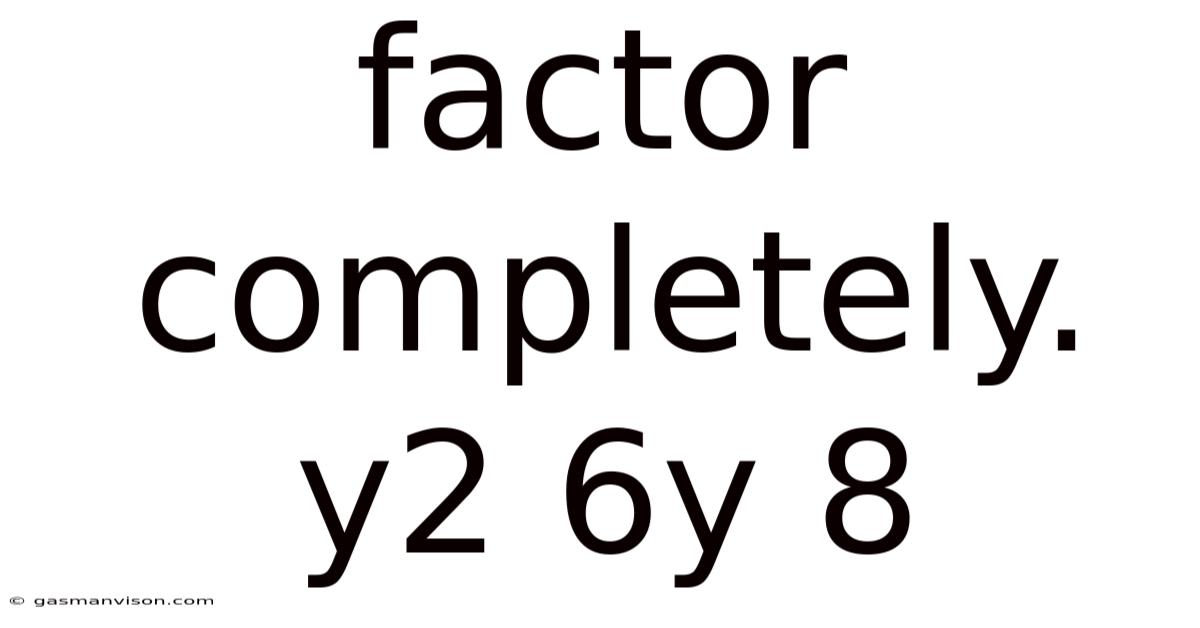
Table of Contents
Factoring Completely: A Deep Dive into y² + 6y + 8
This article provides a comprehensive guide to factoring the quadratic expression y² + 6y + 8 completely. We'll explore various factoring methods, delve into the underlying mathematical principles, and address common misconceptions. Understanding this seemingly simple problem unlocks a deeper understanding of algebra and lays the groundwork for more complex polynomial manipulations. This guide is designed for students, educators, and anyone looking to refresh their factoring skills.
Meta Description: Learn how to completely factor the quadratic expression y² + 6y + 8. This detailed guide covers multiple factoring methods, explains the underlying mathematical principles, and addresses common mistakes. Improve your algebra skills and master polynomial factoring!
Understanding Quadratic Expressions
Before diving into the factoring process, let's establish a solid understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'y') is 2. The general form of a quadratic expression is:
ax² + bx + c
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our example, y² + 6y + 8, we have a = 1, b = 6, and c = 8.
Method 1: Factoring by Inspection (Trial and Error)
This method involves finding two numbers that satisfy two conditions:
- Their product equals 'c' (the constant term): In our case, the product must be 8.
- Their sum equals 'b' (the coefficient of the linear term): In our case, the sum must be 6.
Let's consider the factors of 8:
- 1 and 8
- 2 and 4
- -1 and -8
- -2 and -4
Only the pair 2 and 4 satisfy both conditions: 2 * 4 = 8 and 2 + 4 = 6.
Therefore, we can factor y² + 6y + 8 as:
(y + 2)(y + 4)
This is the completely factored form of the expression. We can verify this by expanding the factored form using the FOIL method (First, Outer, Inner, Last):
(y + 2)(y + 4) = y² + 4y + 2y + 8 = y² + 6y + 8
This confirms our factorization is correct.
Method 2: AC Method (for more complex quadratics)
The AC method is a more systematic approach, particularly useful when dealing with quadratic expressions where 'a' is not equal to 1. While not strictly necessary for y² + 6y + 8, it's a valuable technique to learn for more challenging problems.
- Find the product AC: In our case, A = 1 and C = 8, so AC = 8.
- Find two numbers that multiply to AC and add to B: We need two numbers that multiply to 8 and add to 6. Again, these are 2 and 4.
- Rewrite the middle term: Rewrite 6y as 2y + 4y: y² + 2y + 4y + 8
- Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair: y(y + 2) + 4(y + 2)
- Factor out the common binomial factor: (y + 2)(y + 4)
This again yields the completely factored form: (y + 2)(y + 4).
Method 3: Completing the Square
Completing the square is a powerful technique used to solve quadratic equations and can also be applied to factoring. While less efficient for this specific problem, it's crucial to understand this method for its broader applications.
- Move the constant term to the right side: y² + 6y = -8
- Take half of the coefficient of the linear term (6y), square it, and add it to both sides: Half of 6 is 3, and 3² = 9. So we add 9 to both sides: y² + 6y + 9 = -8 + 9 y² + 6y + 9 = 1
- Factor the perfect square trinomial: The left side is now a perfect square trinomial, which factors as (y + 3)². (y + 3)² = 1
- Take the square root of both sides: y + 3 = ±√1 = ±1
- Solve for y: y = -3 ± 1, which gives y = -2 and y = -4.
- Rewrite in factored form: Since y = -2 and y = -4 are the roots, the factored form is (y + 2)(y + 4).
This method, although more involved, demonstrates another pathway to achieving the same factored result.
Understanding the Significance of Factoring
Completely factoring a quadratic expression like y² + 6y + 8 is not just an algebraic exercise; it holds significant importance in various mathematical contexts:
-
Solving Quadratic Equations: Factoring allows us to easily solve quadratic equations. Setting the factored expression equal to zero, (y + 2)(y + 4) = 0, allows us to find the roots (or zeros) of the equation: y = -2 and y = -4. These values are where the quadratic graph intersects the x-axis.
-
Graphing Quadratic Functions: The factored form reveals the x-intercepts of the parabola represented by the quadratic function y = y² + 6y + 8. These intercepts are crucial for sketching the graph accurately. The vertex of the parabola can also be found using the factored form or other methods.
-
Simplifying Expressions: Factoring simplifies more complex algebraic expressions. It can be used to cancel out common factors, simplifying fractions and other mathematical operations involving polynomials.
-
Further Algebraic Manipulations: Factoring is a fundamental skill used in calculus, particularly in integral and differential calculus, for simplifying expressions and solving problems.
Common Mistakes to Avoid
-
Incorrect Signs: Pay close attention to the signs when choosing factors. Ensure the product and sum of the chosen factors match the constant and coefficient terms correctly.
-
Missing Factors: Always check if there are any common factors among the terms before applying factoring methods. Sometimes, a common factor can be factored out first, simplifying the expression.
-
Incomplete Factoring: Make sure the expression is factored completely. Sometimes, factors themselves might be further factorable.
-
Not Checking Your Work: Always verify your factorization by expanding the factored form using the FOIL method or distribution to ensure it matches the original expression.
Conclusion
Factoring the quadratic expression y² + 6y + 8 completely results in (y + 2)(y + 4). This seemingly simple problem highlights fundamental concepts in algebra and provides a solid foundation for tackling more complex polynomial manipulations. Mastering various factoring methods, understanding their applications, and avoiding common mistakes are essential for success in algebra and beyond. The ability to factor completely opens doors to solving quadratic equations, graphing quadratic functions, simplifying expressions, and tackling advanced mathematical concepts with greater ease and confidence. Remember to practice regularly and utilize different methods to solidify your understanding and build proficiency in factoring.
Latest Posts
Latest Posts
-
What Is 60ml In Oz
Sep 24, 2025
-
Air Pressure Is Highest When
Sep 24, 2025
-
A Phylogenetic Tree Is Arranged
Sep 24, 2025
-
Partial Charges Occur When
Sep 24, 2025
-
Sternbergs Triangular Theory Of Love
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Factor Completely. Y2 6y 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.