Factor X 2 3x 28
gasmanvison
Sep 13, 2025 · 5 min read
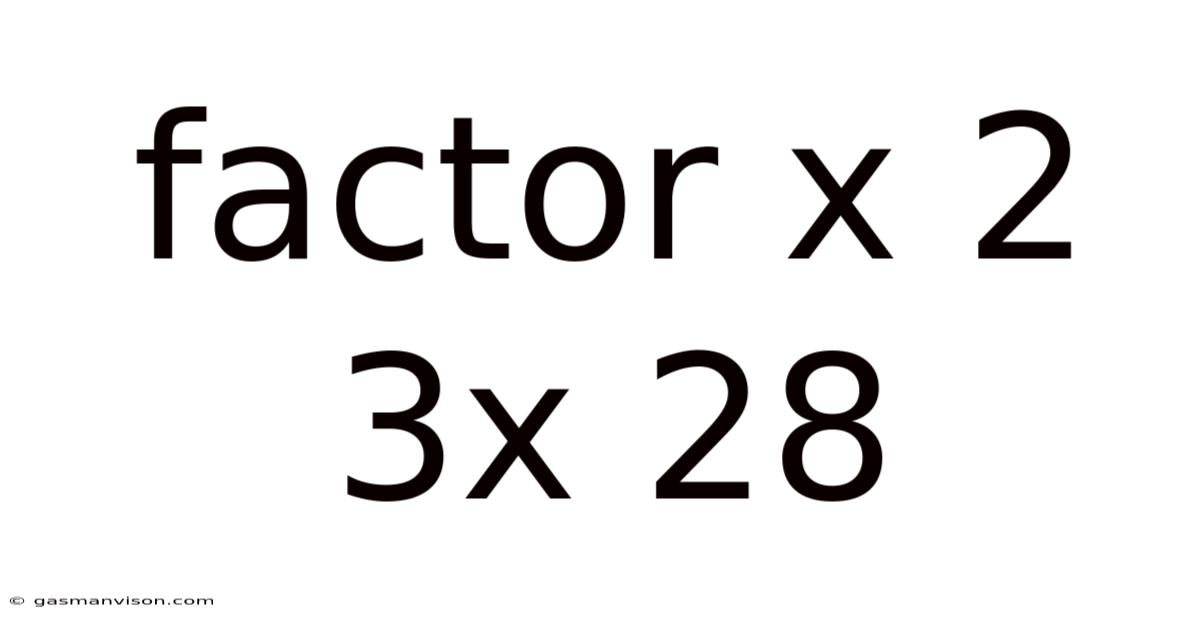
Table of Contents
Deconstructing the Quadratic: A Deep Dive into Factoring x² + 3x - 28
This article will provide a comprehensive exploration of factoring the quadratic expression x² + 3x - 28. We'll move beyond simply providing the answer, delving into the underlying principles, different methods for solving it, and connecting it to broader mathematical concepts. Understanding this seemingly simple problem unlocks a deeper understanding of algebra and its applications.
What is Factoring?
Before diving into the specifics of x² + 3x - 28, let's establish a foundational understanding of factoring. In mathematics, factoring involves expressing a mathematical expression as a product of simpler expressions. Think of it as the reverse of expanding brackets (or using the distributive property). For example, expanding (x + 2)(x + 1) gives us x² + 3x + 2. Factoring x² + 3x + 2 would then give us (x + 2)(x + 1). Factoring simplifies expressions, making them easier to work with and revealing underlying structures. It's a crucial skill in algebra, calculus, and numerous other areas of mathematics.
Approaches to Factoring x² + 3x - 28
Several methods can be employed to factor x² + 3x - 28. We'll explore the most common and effective ones:
1. The AC Method (or Factoring by Grouping)
This method is particularly useful for factoring quadratic expressions in the form ax² + bx + c, where a, b, and c are constants. In our case, a = 1, b = 3, and c = -28.
-
Step 1: Find the product 'ac'. In this case, ac = 1 * -28 = -28.
-
Step 2: Find two numbers that add up to 'b' (3) and multiply to 'ac' (-28). These numbers are 7 and -4 because 7 + (-4) = 3 and 7 * (-4) = -28.
-
Step 3: Rewrite the middle term using these two numbers. We rewrite 3x as 7x - 4x: x² + 7x - 4x - 28
-
Step 4: Factor by grouping. Group the first two terms and the last two terms: (x² + 7x) + (-4x - 28)
-
Step 5: Factor out the greatest common factor (GCF) from each group. The GCF of x² + 7x is x, and the GCF of -4x - 28 is -4: x(x + 7) - 4(x + 7)
-
Step 6: Factor out the common binomial factor. Both terms now share the factor (x + 7): (x + 7)(x - 4)
Therefore, the factored form of x² + 3x - 28 is (x + 7)(x - 4).
2. The Trial and Error Method
This method involves systematically trying different pairs of factors until you find the correct combination. It's often faster for simpler quadratics where a = 1.
Since the coefficient of x² is 1, we know the factors will be of the form (x + p)(x + q), where p and q are constants. We need to find p and q such that p + q = 3 (the coefficient of x) and pq = -28 (the constant term). Through trial and error (considering factor pairs of -28 like 1 and -28, 2 and -14, 4 and -7, etc.), we quickly discover that 7 and -4 satisfy these conditions. Thus, we arrive at the same factored form: (x + 7)(x - 4).
3. Using the Quadratic Formula
While primarily used to find the roots (or zeros) of a quadratic equation, the quadratic formula can indirectly help with factoring. The quadratic formula states:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 3x - 28, a = 1, b = 3, and c = -28. Plugging these values into the formula gives us:
x = [-3 ± √(3² - 4 * 1 * -28)] / 2 * 1 = [-3 ± √121] / 2 = [-3 ± 11] / 2
This gives us two solutions: x = 4 and x = -7. Since the roots of a quadratic equation are related to its factors, we can express the factored form as (x - 4)(x + 7), which is the same result as before. This method is less efficient for factoring directly but highlights the connection between roots and factors.
Understanding the Significance of Factoring
Factoring x² + 3x - 28 is more than just an algebraic exercise. It's a fundamental skill with numerous applications:
-
Solving Quadratic Equations: Setting x² + 3x - 28 = 0 allows us to find the x-intercepts (roots or zeros) of the corresponding quadratic function. These are the values of x where the graph of the function crosses the x-axis. In our case, the roots are x = 4 and x = -7.
-
Simplifying Expressions: Factoring simplifies complex expressions, making them easier to manipulate and analyze. This is crucial in simplifying rational expressions (fractions with polynomials) and in calculus.
-
Graphing Quadratic Functions: The factored form reveals the x-intercepts, which are key points in graphing a parabola (the shape of a quadratic function). Knowing the x-intercepts and the vertex (the highest or lowest point on the parabola) helps to accurately sketch the graph.
-
Solving Real-World Problems: Quadratic equations model many real-world phenomena, including projectile motion, area calculations, and optimization problems. Factoring is instrumental in solving these problems. For example, if the area of a rectangular garden is represented by x² + 3x - 28 square meters, factoring helps determine the possible dimensions of the garden (x + 7 meters and x - 4 meters).
Expanding on the Concept: More Complex Quadratics
While x² + 3x - 28 is a relatively simple quadratic, the principles we've discussed extend to more complex scenarios. Consider quadratics where 'a' is not equal to 1, or those involving irrational or complex roots. The AC method remains a powerful approach, even with more challenging expressions. However, understanding the underlying principles of factoring remains key.
Conclusion: Mastering the Fundamentals
Mastering the art of factoring quadratic expressions like x² + 3x - 28 is essential for success in algebra and beyond. By understanding different factoring techniques and connecting them to the broader context of quadratic equations and their applications, you build a solid foundation for tackling more advanced mathematical concepts. The seemingly simple task of factoring this quadratic expression provides a stepping stone to a deeper comprehension of fundamental algebraic principles and their widespread utility. Remember to practice regularly, exploring different problems and challenging yourself with increasingly complex quadratics. This will solidify your understanding and prepare you for more advanced mathematical studies.
Latest Posts
Latest Posts
-
Nad Medical Abbreviation Physical Exam
Sep 14, 2025
-
How Tall Is 73 Inches
Sep 14, 2025
-
Water Has Surface Tension Because
Sep 14, 2025
-
How Long Is 26 Inches
Sep 14, 2025
-
Convert 30 Ml To Oz
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 3x 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.