Factor X 2 4x 5
gasmanvison
Sep 16, 2025 · 5 min read
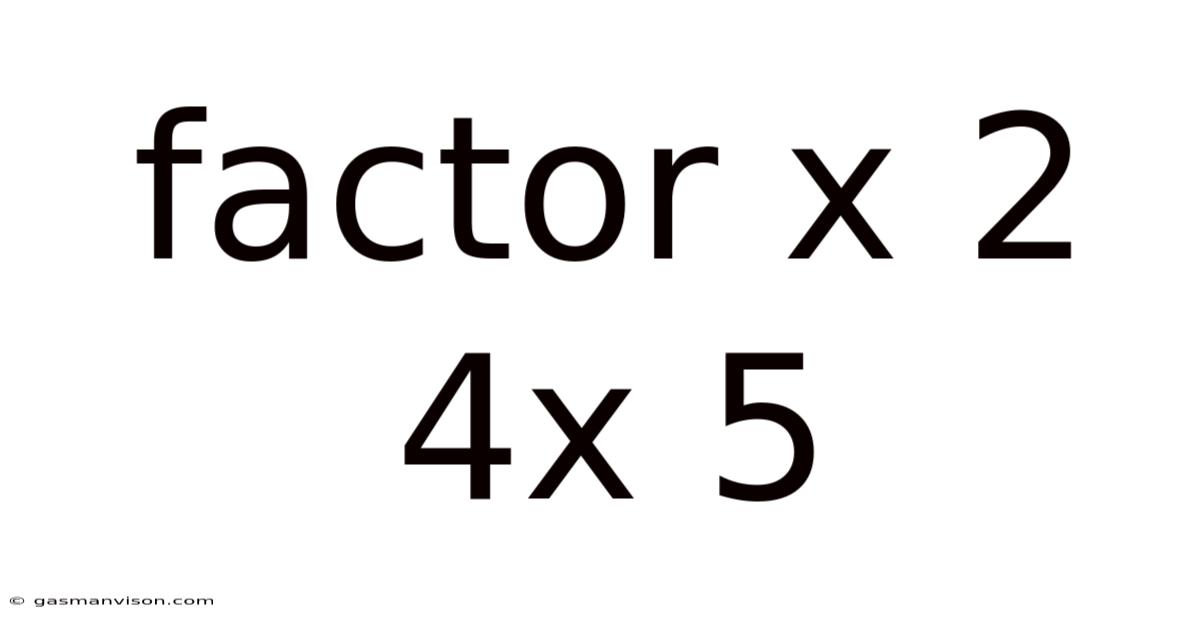
Table of Contents
Unraveling the Mysteries of Factor X² + 4X + 5: A Deep Dive into Quadratic Expressions
This article delves into the intricacies of the quadratic expression x² + 4x + 5, exploring its properties, solving methods, and applications. We'll move beyond simply finding the roots and uncover the deeper mathematical significance of this seemingly simple equation. Understanding this expression provides a strong foundation for tackling more complex quadratic problems and related concepts in algebra and beyond. This comprehensive guide will equip you with the tools to not only solve this specific expression but also to approach similar quadratic equations with confidence.
What is a Quadratic Expression?
Before we dive into the specifics of x² + 4x + 5, let's establish a fundamental understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our expression, x² + 4x + 5, fits this form perfectly, with a = 1, b = 4, and c = 5.
Finding the Roots: The Quest for Solutions
The "roots" or "zeros" of a quadratic expression are the values of x that make the expression equal to zero. These values represent the points where the parabola (the graph of a quadratic equation) intersects the x-axis. There are several methods to find the roots of a quadratic equation, including:
-
Factoring: This involves rewriting the quadratic expression as a product of two linear expressions. However, not all quadratic expressions can be factored easily using integer coefficients. In the case of x² + 4x + 5, factoring with real numbers is not possible.
-
Quadratic Formula: This is a powerful and universally applicable method for finding the roots of any quadratic equation. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression, a = 1, b = 4, and c = 5. Plugging these values into the quadratic formula, we get:
x = [-4 ± √(4² - 4 * 1 * 5)] / 2 * 1 x = [-4 ± √(16 - 20)] / 2 x = [-4 ± √(-4)] / 2 x = [-4 ± 2i] / 2 x = -2 ± i
Notice that the roots are complex numbers, involving the imaginary unit 'i', where i² = -1. This indicates that the parabola representing this quadratic expression does not intersect the x-axis in the real plane.
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, which can then be easily factored. While applicable, it's less efficient than the quadratic formula in this particular case.
The Discriminant: A Window into the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. The discriminant provides valuable information about the nature of the roots:
-
b² - 4ac > 0: The quadratic equation has two distinct real roots. The parabola intersects the x-axis at two different points.
-
b² - 4ac = 0: The quadratic equation has one real root (a repeated root). The parabola touches the x-axis at exactly one point.
-
b² - 4ac < 0: The quadratic equation has two complex conjugate roots, as we found in our example. The parabola does not intersect the x-axis in the real plane.
In our case, the discriminant is 16 - 20 = -4, which is less than zero, confirming the presence of two complex conjugate roots.
Graphical Representation: Visualizing the Parabola
Visualizing the quadratic expression as a parabola helps understand its behavior. Since the coefficient of x² (a = 1) is positive, the parabola opens upwards. The vertex of the parabola, the lowest point, can be found using the formula:
x = -b / 2a = -4 / 2(1) = -2
Substituting x = -2 back into the equation gives the y-coordinate of the vertex:
y = (-2)² + 4(-2) + 5 = 1
Therefore, the vertex of the parabola is at (-2, 1). Because the parabola opens upwards and the vertex is above the x-axis, it doesn't intersect the x-axis, aligning with our finding of complex roots.
Applications of Quadratic Expressions:
Quadratic equations and expressions have wide-ranging applications across various fields, including:
-
Physics: Modeling projectile motion, calculating the trajectory of objects under gravity, and analyzing oscillations.
-
Engineering: Designing structures, optimizing processes, and solving problems related to stress and strain.
-
Economics: Analyzing market trends, predicting consumer behavior, and modeling economic growth.
-
Computer Science: Developing algorithms, optimizing computer programs, and solving computational problems.
-
Finance: Calculating compound interest, determining investment returns, and analyzing financial models.
Further Exploration: Extending the Understanding
Understanding x² + 4x + 5 lays a foundation for delving into more complex concepts:
-
Complex Numbers: The presence of complex roots opens up the fascinating world of complex numbers, with their unique properties and applications.
-
Quadratic Transformations: Exploring how transformations like shifting, stretching, and reflecting affect the graph of the parabola.
-
Polynomial Equations of Higher Degree: Extending the understanding of solving methods to cubic, quartic, and higher-degree polynomial equations.
Conclusion:
The seemingly simple quadratic expression x² + 4x + 5 provides a rich landscape for exploration, highlighting the power of algebraic manipulation and the beauty of mathematical concepts. By understanding its roots, graphical representation, and the implications of the discriminant, we gain a deeper appreciation for the broader field of algebra and its diverse applications. While this specific quadratic doesn't yield real number solutions, the process of solving it reinforces crucial problem-solving skills applicable to a multitude of mathematical challenges. The exploration undertaken here provides a robust foundation for tackling more advanced algebraic concepts and their real-world applications. Remember, the journey of mathematical understanding is continuous, and this is just one step in that exciting process.
Latest Posts
Latest Posts
-
Castor Oil Vs Mineral Oil
Sep 16, 2025
-
What Is 15 Of 600
Sep 16, 2025
-
Combine And Simplify These Radicals
Sep 16, 2025
-
17 3 As A Mixed Number
Sep 16, 2025
-
Three Components Of A Nucleotide
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 4x 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.