Factor X 2 6x 9
gasmanvison
Sep 16, 2025 · 5 min read
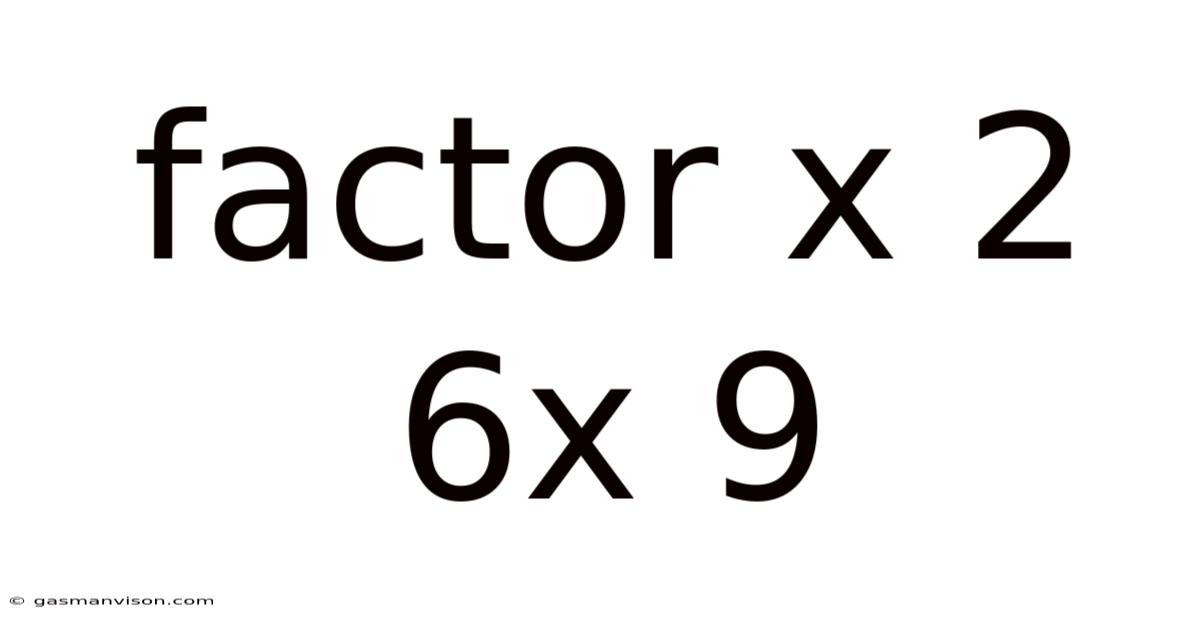
Table of Contents
Factoring x² + 6x + 9: A Comprehensive Guide
This article delves into the process of factoring the quadratic expression x² + 6x + 9, exploring various methods and providing a deeper understanding of the underlying mathematical concepts. We will not only demonstrate how to factor this specific expression but also equip you with the skills to tackle similar quadratic equations. Understanding quadratic factoring is crucial for various mathematical applications, including solving quadratic equations, simplifying algebraic expressions, and even in advanced calculus.
Understanding Quadratic Expressions
Before we dive into factoring x² + 6x + 9, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our example, x² + 6x + 9, a = 1, b = 6, and c = 9.
Method 1: Factoring by Recognizing a Perfect Square Trinomial
The expression x² + 6x + 9 is a special case of a quadratic expression known as a perfect square trinomial. A perfect square trinomial is a trinomial (a three-term polynomial) that can be factored into the square of a binomial. Let's examine its characteristics:
- The first term (x²) is a perfect square: x² = (x)²
- The last term (9) is a perfect square: 9 = (3)²
- The middle term (6x) is twice the product of the square roots of the first and last terms: 2 * x * 3 = 6x
Because all three conditions are met, x² + 6x + 9 is a perfect square trinomial. This means it can be factored directly as:
(x + 3)²
This is equivalent to (x + 3)(x + 3). You can verify this by expanding the factored form using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * 3 = 3x
- Inner: 3 * x = 3x
- Last: 3 * 3 = 9
Adding these terms together gives us x² + 3x + 3x + 9 = x² + 6x + 9, confirming our factorization.
Method 2: Factoring by Using the Quadratic Formula
While the perfect square trinomial method is the most efficient approach for this particular expression, understanding the quadratic formula provides a more general solution for factoring any quadratic expression. The quadratic formula is used to find the roots (or zeros) of a quadratic equation, which are the values of x that make the expression equal to zero. These roots are directly related to the factors of the quadratic expression.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 6x + 9, a = 1, b = 6, and c = 9. Substituting these values into the quadratic formula, we get:
x = [-6 ± √(6² - 4 * 1 * 9)] / (2 * 1) x = [-6 ± √(36 - 36)] / 2 x = [-6 ± √0] / 2 x = -6 / 2 x = -3
Since we only have one root (x = -3), this indicates that the quadratic expression has a repeated root, further confirming that it's a perfect square trinomial. The factor is (x - (-3)) = (x + 3). Because it's a repeated root, the factored form is (x + 3)(x + 3) or (x + 3)².
Method 3: Factoring by Grouping (Less Efficient for this Example)
Factoring by grouping is a method used for factoring polynomials with four or more terms. Although less efficient for this particular trinomial, we can demonstrate the process for educational purposes. To use this method on a trinomial, we would need to rewrite it as a four-term polynomial. This isn't straightforward for x² + 6x + 9 and is generally not recommended for trinomials that are perfect squares.
Solving Quadratic Equations using the Factored Form
Once we have factored x² + 6x + 9 as (x + 3)², we can use this factored form to solve the quadratic equation x² + 6x + 9 = 0. Setting the factored form equal to zero, we get:
(x + 3)² = 0
Taking the square root of both sides:
x + 3 = 0
Solving for x:
x = -3
This confirms that -3 is the root of the equation.
Applications of Factoring Quadratic Expressions
The ability to factor quadratic expressions has numerous applications in various fields:
- Algebra: Simplifying complex algebraic expressions, solving quadratic equations, and finding the roots of polynomial functions.
- Calculus: Finding critical points, determining concavity, and solving optimization problems.
- Physics: Modeling projectile motion, analyzing oscillations, and studying the behavior of systems described by quadratic equations.
- Engineering: Designing structures, analyzing circuits, and modeling various physical phenomena.
- Economics: Analyzing cost functions, profit maximization, and market equilibrium.
Expanding Your Understanding: Factoring Other Quadratic Expressions
While x² + 6x + 9 is a relatively straightforward example, the principles discussed here apply to a broader range of quadratic expressions. To factor other quadratic expressions, consider the following:
- Look for common factors: Before attempting any factorization method, check for common factors among the terms. If present, factor them out first.
- Recognize special cases: Look for perfect square trinomials, difference of squares, and sum/difference of cubes.
- Use the quadratic formula: If other methods fail, the quadratic formula always provides a solution. Remember that the roots of the equation will directly relate to the factors.
- Practice regularly: Consistent practice is key to mastering quadratic factoring. Work through various examples, starting with simpler expressions and progressively tackling more complex ones.
Advanced Concepts: Complex Roots and Discriminant
For some quadratic expressions, the discriminant (the term b² - 4ac within the quadratic formula) may be negative. This indicates that the quadratic equation has complex roots (involving imaginary numbers). While the factorization might not be directly evident in the real number system, understanding complex numbers is crucial for a complete understanding of quadratic equations and their solutions.
Conclusion:
Factoring x² + 6x + 9, as a perfect square trinomial, highlights the efficiency of recognizing special patterns in mathematics. This article provides not only the solution but also a comprehensive understanding of the underlying mathematical principles involved in factoring quadratic expressions, laying a solid foundation for further exploration of algebraic concepts and their applications. Remember that consistent practice and a methodical approach are key to mastering this essential mathematical skill. By understanding different factoring techniques and their application, you can confidently tackle a wide range of algebraic problems.
Latest Posts
Latest Posts
-
Convert 175 C To Fahrenheit
Sep 16, 2025
-
10 0 4 0 5 G 4g
Sep 16, 2025
-
Subject Complements Are Words That
Sep 16, 2025
-
Crossword Puzzle For Respiratory System
Sep 16, 2025
-
20 Twenty Sevens Minus 1 Twenty Seven
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 6x 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.