Factor X 2 8x 16
gasmanvison
Sep 19, 2025 · 5 min read
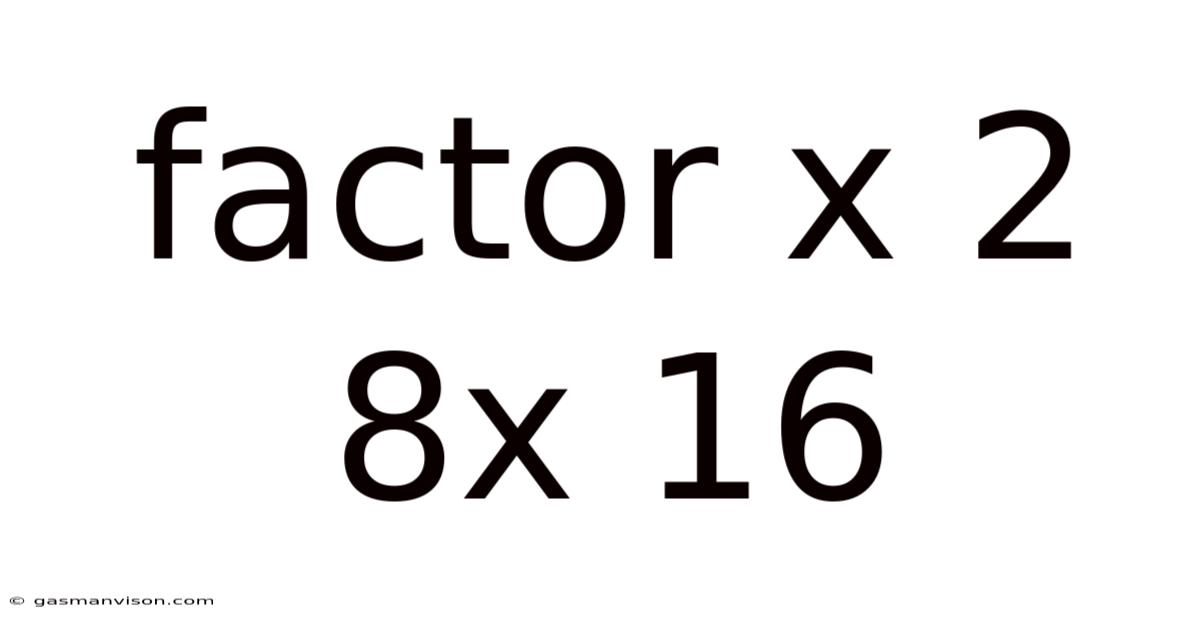
Table of Contents
Unraveling the Mystery of Factor X² - 8X + 16: A Deep Dive into Quadratic Expressions
This article delves into the quadratic expression x² - 8x + 16, exploring its factorization, its graphical representation, its roots, and its applications in various mathematical contexts. Understanding this seemingly simple expression unlocks a deeper comprehension of quadratic equations and their significance in algebra and beyond. This comprehensive guide will equip you with the knowledge and tools to not only solve this specific expression but also tackle similar problems with confidence.
What is a Quadratic Expression?
Before we dive into the specifics of x² - 8x + 16, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (typically 'x') is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and 'a' is not equal to zero. Our expression, x² - 8x + 16, fits this form perfectly, with a = 1, b = -8, and c = 16.
Factoring the Quadratic Expression: x² - 8x + 16
Factoring a quadratic expression involves finding two binomials whose product equals the original expression. This process simplifies the expression and allows for easier manipulation and problem-solving. There are several methods to factor quadratic expressions, and we'll explore a few approaches to factor x² - 8x + 16.
Method 1: The AC Method
This method is particularly useful when the coefficient of x² (a) is not equal to 1. However, it works perfectly well for our expression as well.
- Identify a, b, and c: In our expression, a = 1, b = -8, and c = 16.
- Find two numbers that multiply to ac and add to b: We need two numbers that multiply to (1)(16) = 16 and add to -8. These numbers are -4 and -4.
- Rewrite the expression: Rewrite the middle term (-8x) using these two numbers: x² - 4x - 4x + 16.
- Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair: x(x - 4) - 4(x - 4).
- Factor out the common binomial: Notice that (x - 4) is common to both terms. Factor it out: (x - 4)(x - 4).
- Simplified Form: The factored form is (x - 4)².
Method 2: Perfect Square Trinomial
Observe that x² - 8x + 16 is a perfect square trinomial. This means it can be factored into the square of a binomial. A perfect square trinomial has the form a² + 2ab + b² or a² - 2ab + b², which factors to (a + b)² or (a - b)², respectively.
In our case:
- x² is the square of x (a = x).
- 16 is the square of 4 (b = 4).
- -8x is twice the product of x and -4 (2ab = 2 * x * -4 = -8x).
Therefore, x² - 8x + 16 factors directly to (x - 4)².
Method 3: Using the Quadratic Formula (for finding roots, not direct factorization)
While not a direct factorization method, the quadratic formula can be used to find the roots of the equation x² - 8x + 16 = 0. The roots are the values of x that make the equation true. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 1, b = -8, c = 16):
x = [8 ± √((-8)² - 4 * 1 * 16)] / 2 * 1 = [8 ± √(64 - 64)] / 2 = 8 / 2 = 4
This reveals that the equation x² - 8x + 16 = 0 has a single, repeated root at x = 4. This confirms our factorization (x - 4)².
Graphical Representation of x² - 8x + 16
The graphical representation of a quadratic expression is a parabola. The parabola's vertex represents the minimum or maximum value of the expression. Since the coefficient of x² (a = 1) is positive, the parabola opens upwards, meaning it has a minimum value.
The vertex of the parabola can be found using the formula x = -b / 2a. In our case:
x = -(-8) / 2 * 1 = 4
Substituting x = 4 back into the expression:
y = (4)² - 8(4) + 16 = 0
Therefore, the vertex of the parabola is at (4, 0). This point is also the x-intercept (where the parabola crosses the x-axis), which corresponds to the root we found earlier. The parabola is tangent to the x-axis at x=4, indicating a repeated root.
Applications of Quadratic Expressions
Quadratic expressions have widespread applications across various fields, including:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing parabolic antennas, bridges, and other structures.
- Economics: Modeling profit, revenue, and cost functions.
- Computer Graphics: Creating curves and shapes in two-dimensional and three-dimensional spaces.
- Statistics: Analyzing data distributions and fitting curves to data points.
Solving Equations Involving x² - 8x + 16
Once we have factored the expression, solving equations becomes straightforward. For example, let's solve the equation:
x² - 8x + 16 = 0
Since we know the factored form is (x - 4)², we can rewrite the equation as:
(x - 4)² = 0
Taking the square root of both sides:
x - 4 = 0
Solving for x:
x = 4
This confirms our previous finding that the equation has a single repeated root at x = 4.
Expanding on the Concept: Variations and Extensions
While we have focused on x² - 8x + 16, the principles discussed apply to a broader range of quadratic expressions. Consider these related examples:
- x² + 8x + 16: This expression factors to (x + 4)². The parabola opens upwards, with its vertex at (-4, 0).
- x² - 8x + 15: This factors to (x - 3)(x - 5). The parabola opens upwards, intersecting the x-axis at x = 3 and x = 5.
- x² + 8x + 7: This factors to (x+1)(x+7). The parabola opens upwards, intersecting the x-axis at x = -1 and x = -7.
Understanding the fundamental concepts of factoring, graphing, and solving quadratic equations provides a strong foundation for tackling more complex mathematical problems. The ability to efficiently factor quadratic expressions is essential for various mathematical applications, and mastering these techniques greatly enhances problem-solving capabilities across numerous fields. The simple quadratic expression x² - 8x + 16, despite its appearance, serves as a powerful example of how seemingly simple algebraic expressions hold profound mathematical significance and far-reaching practical applications.
Latest Posts
Latest Posts
-
Who Was The Nun Guda
Sep 19, 2025
-
Radio Set An Vrc 90f
Sep 19, 2025
-
An Activist Would Most Likely
Sep 19, 2025
-
25 X 40 X 4
Sep 19, 2025
-
What Is 3 4 Plus 3 4
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 8x 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.