Factorise X 2 4x 12
gasmanvison
Sep 11, 2025 · 5 min read
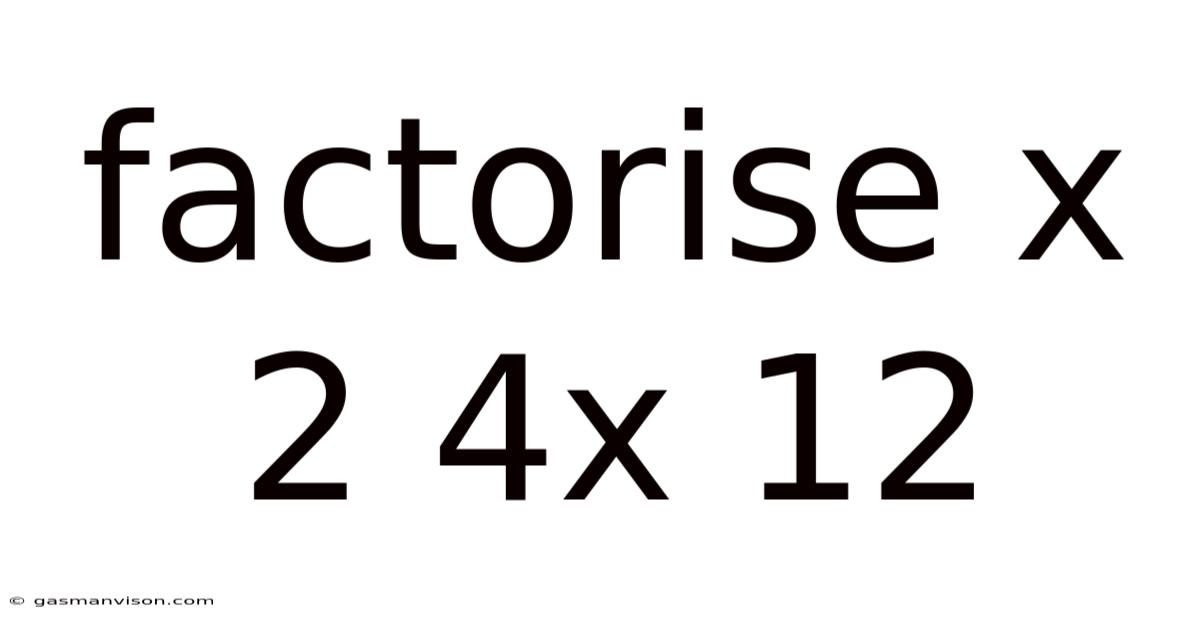
Table of Contents
Factorising Quadratic Expressions: A Deep Dive into x² + 4x + 12
This article provides a comprehensive guide to factorising the quadratic expression x² + 4x + 12, exploring various methods and delving into the underlying mathematical concepts. We'll examine why simple factoring techniques fail in this specific case, and then explore alternative approaches to understand the nature of the expression's roots. This will not only help you solve this particular problem but also equip you with the skills to tackle similar quadratic equations effectively. Understanding quadratic factorisation is crucial for higher-level mathematics and numerous applications in science and engineering.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. Factorising a quadratic expression means rewriting it as a product of two linear expressions. This process is fundamental in solving quadratic equations and simplifying algebraic expressions.
Attempting Standard Factorisation
Let's first try the standard method of factorisation, which involves finding two numbers that add up to the coefficient of x (b = 4 in this case) and multiply to the constant term (c = 12). We need two numbers that add to 4 and multiply to 12. Let's consider the pairs of factors of 12:
- 1 and 12 (sum = 13)
- 2 and 6 (sum = 8)
- 3 and 4 (sum = 7)
None of these pairs add up to 4. This indicates that the quadratic expression x² + 4x + 12 cannot be factorised using simple integer factors. This doesn't mean it's unfactorisable; it simply means the factors are not simple integers.
Exploring Alternative Methods: The Quadratic Formula
Since simple factorisation fails, we can employ the quadratic formula to find the roots of the corresponding quadratic equation x² + 4x + 12 = 0. The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our case, a = 1, b = 4, and c = 12. Substituting these values into the quadratic formula, we get:
x = [-4 ± √(4² - 4 * 1 * 12)] / 2 * 1 x = [-4 ± √(16 - 48)] / 2 x = [-4 ± √(-32)] / 2
Notice that we have a negative number under the square root. This means the roots of the equation are complex numbers, involving the imaginary unit 'i', where i² = -1.
Understanding Complex Numbers and Their Role in Factorisation
The expression √(-32) can be simplified as follows:
√(-32) = √(16 * -2) = √16 * √-2 = 4√-2 = 4i√2
Therefore, the roots of the quadratic equation are:
x = (-4 + 4i√2) / 2 = -2 + 2i√2 x = (-4 - 4i√2) / 2 = -2 - 2i√2
These are the two complex roots of the quadratic equation. Since we have found the roots, we can now express the quadratic expression in its factorised form using these roots:
x² + 4x + 12 = (x - (-2 + 2i√2))(x - (-2 - 2i√2)) x² + 4x + 12 = (x + 2 - 2i√2)(x + 2 + 2i√2)
This is the complete factorisation of the quadratic expression, showcasing its complex roots.
Completing the Square: An Alternative Approach
Another method to solve quadratic equations is completing the square. This technique involves manipulating the quadratic expression to create a perfect square trinomial. The steps are as follows:
- Group the x terms: x² + 4x + 12
- Take half of the coefficient of x (4/2 = 2) and square it (2² = 4): This is the value we will use to complete the square.
- Add and subtract the value obtained in step 2: x² + 4x + 4 - 4 + 12
- Rewrite the first three terms as a perfect square: (x + 2)² - 4 + 12
- Simplify: (x + 2)² + 8
This gives us the quadratic expression in vertex form: (x + 2)² + 8 = 0. Solving for x would again yield the same complex roots we obtained using the quadratic formula. This confirms that the expression cannot be factored into simple real number expressions.
The Discriminant and the Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. It determines the nature of the roots of the quadratic equation:
- If b² - 4ac > 0: The equation has two distinct real roots.
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has two distinct complex roots (conjugate pairs).
In our case, b² - 4ac = 16 - 48 = -32, which is less than 0. This confirms that our quadratic expression has two distinct complex roots, as we have already found.
Graphical Representation and Understanding the Roots
Graphing the quadratic function y = x² + 4x + 12 reveals a parabola that opens upwards (since the coefficient of x² is positive). Crucially, the parabola lies entirely above the x-axis. This means the quadratic equation y = x² + 4x + 12 = 0 has no real roots; the parabola never intersects the x-axis. The complex roots we found represent the points where the parabola would intersect the x-axis in the complex plane.
Applications of Complex Numbers and Quadratic Factorisation
While seemingly abstract, complex numbers and the factorisation of quadratic expressions with complex roots have practical applications in various fields:
- Electrical Engineering: Complex numbers are used extensively in analyzing alternating current (AC) circuits. Impedance, a measure of opposition to current flow, is often represented as a complex number.
- Signal Processing: Complex numbers are crucial in the analysis and manipulation of signals, such as sound waves and radio waves. The Fourier transform, a powerful tool in signal processing, relies heavily on complex numbers.
- Quantum Mechanics: Complex numbers are fundamental to the mathematical framework of quantum mechanics, describing the wave function of particles.
- Fluid Dynamics: Complex analysis helps solve problems in fluid flow and potential theory.
Conclusion: Mastering Quadratic Factorisation
Factorising the quadratic expression x² + 4x + 12 presents a valuable learning opportunity. While simple integer factorisation isn't possible, the use of the quadratic formula and completing the square reveal its complex roots and allow for a complete factorisation. Understanding the discriminant helps predict the nature of the roots, and the graphical representation provides visual insight. This exploration highlights the importance of complex numbers and their pervasive applications in various scientific and engineering disciplines. By mastering these techniques, you enhance your problem-solving skills in algebra and prepare yourself for more advanced mathematical concepts. Remember, the inability to factor using simple methods doesn’t imply an expression is unfactorisable; it merely indicates the nature of its roots and requires the application of more sophisticated techniques.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factorise X 2 4x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.