Gcf Of 12 And 42
gasmanvison
Sep 15, 2025 · 6 min read
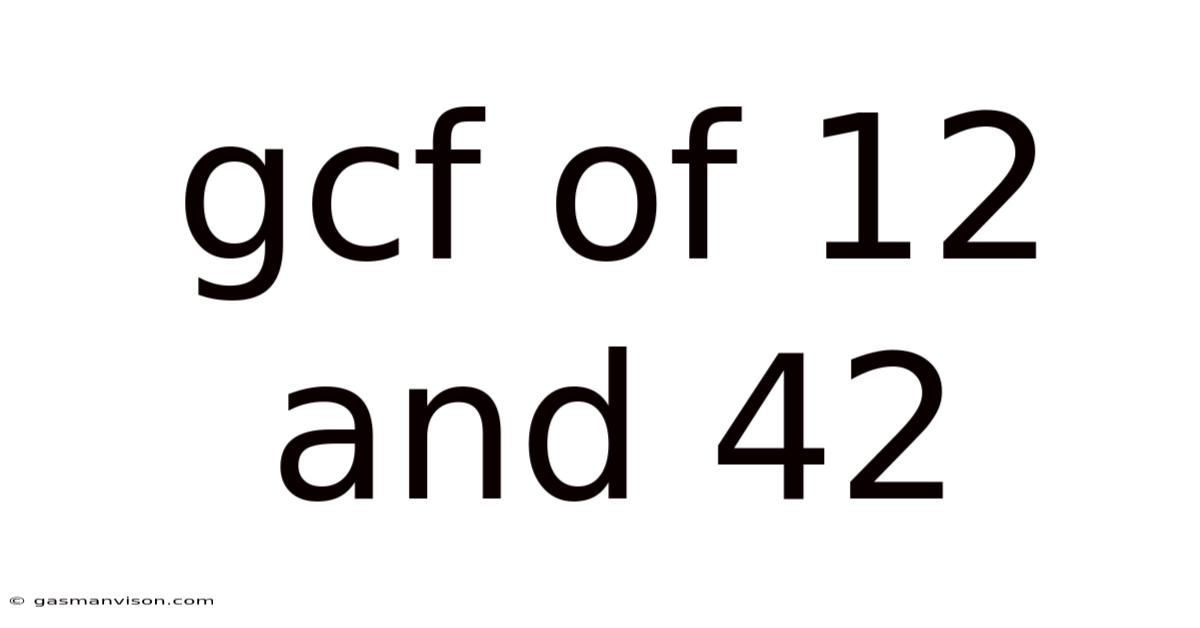
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 12 and 42: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications ranging from simplifying fractions to solving complex algebraic problems. This article delves into the various methods for calculating the GCF of 12 and 42, providing a comprehensive understanding of the underlying principles and showcasing different approaches, from prime factorization to the Euclidean algorithm. We will also explore the practical applications and significance of GCF in various mathematical contexts.
Meta Description: Learn how to find the greatest common factor (GCF) of 12 and 42 using multiple methods, including prime factorization and the Euclidean algorithm. This in-depth guide explores the concept of GCF and its applications in mathematics.
Understanding the Greatest Common Factor (GCF)
Before we jump into calculating the GCF of 12 and 42, let's solidify our understanding of what a GCF actually represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 6 and 9 is 3 because 3 is the largest number that divides both 6 and 9 without any remainder.
Method 1: Prime Factorization
The prime factorization method is a reliable and intuitive approach to finding the GCF. It involves breaking down each number into its prime factors – the smallest positive integers that only divide by 1 and themselves. Let's apply this to 12 and 42:
- Prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Prime factorization of 42: 42 = 2 x 3 x 7
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. In this case, both 12 and 42 share the prime factors 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF of 12 and 42 is 2 x 3 = 6.
This method is particularly useful for visualizing the shared factors and is readily applicable to finding the GCF of more than two numbers. However, for larger numbers, finding the prime factorization can become time-consuming.
Method 2: Listing Factors
A more straightforward (though potentially less efficient for larger numbers) method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
By comparing the two lists, we observe that the common factors are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 42 is 6. This method, while simple, becomes less practical as the numbers get larger due to the increasing number of factors to consider.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, especially when dealing with larger numbers. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 12 and 42:
- Start with the larger number (42) and the smaller number (12).
- Divide the larger number by the smaller number and find the remainder: 42 ÷ 12 = 3 with a remainder of 6.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (6).
- Repeat step 2: 12 ÷ 6 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 6.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers, making it a preferred method in computer science and other fields requiring frequent GCF calculations.
Applications of GCF
The concept of the greatest common factor has numerous applications across various mathematical domains and real-world scenarios:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 12/42 can be simplified by dividing both the numerator and the denominator by their GCF, which is 6, resulting in the simplified fraction 2/7.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations where the solutions are restricted to integers. GCF plays a significant role in determining the solvability and finding integer solutions to these equations.
-
Modular Arithmetic: GCF is essential in understanding modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). This has applications in cryptography and computer science.
-
Geometry: GCF is used in geometric problems involving finding the dimensions of objects that can be divided into smaller, identical units. For example, finding the largest square tiles that can perfectly cover a rectangular floor.
-
Music Theory: GCF helps in understanding musical intervals and harmonies by finding the greatest common divisor of the frequencies of notes.
-
Computer Science: The Euclidean algorithm, which efficiently calculates the GCF, is a fundamental algorithm used in various areas of computer science, including cryptography and data structures.
Beyond 12 and 42: Extending the Concepts
The methods described above can be generalized to find the GCF of any two (or more) integers. For example, let's consider finding the GCF of 24, 36, and 60:
Method 1: Prime Factorization:
- 24 = 2³ x 3
- 36 = 2² x 3²
- 60 = 2² x 3 x 5
The common prime factors are 2 and 3. The lowest power of 2 is 2², and the lowest power of 3 is 3¹. Therefore, the GCF(24, 36, 60) = 2² x 3 = 12.
Method 2: Euclidean Algorithm (for multiple numbers):
While the Euclidean algorithm is primarily designed for two numbers, we can extend it by finding the GCF of two numbers at a time. First, find the GCF of 24 and 36 (which is 12). Then, find the GCF of the result (12) and the third number (60), which is also 12. Therefore, GCF(24, 36, 60) = 12.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with widespread applications. This article has explored three key methods – prime factorization, listing factors, and the Euclidean algorithm – for determining the GCF, illustrating their application using the example of 12 and 42. Understanding these methods empowers you to tackle various mathematical problems and appreciate the elegance and practicality of number theory. The Euclidean algorithm, in particular, stands out as an efficient and robust approach, especially when dealing with larger numbers or complex scenarios. Mastering these techniques will solidify your mathematical foundation and open doors to more advanced concepts in number theory and related fields. Remember that understanding the underlying principles is as crucial as knowing the mechanics of calculation.
Latest Posts
Latest Posts
-
Correlation In A Scatter Plot
Sep 15, 2025
-
Unless Prohibited By A Sign
Sep 15, 2025
-
Lewis Dot Structure For Icl5
Sep 15, 2025
-
What Is 20 Of 720
Sep 15, 2025
-
Whats 48 Inches In Feet
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.