Gcf Of 16 And 32
gasmanvison
Sep 12, 2025 · 6 min read
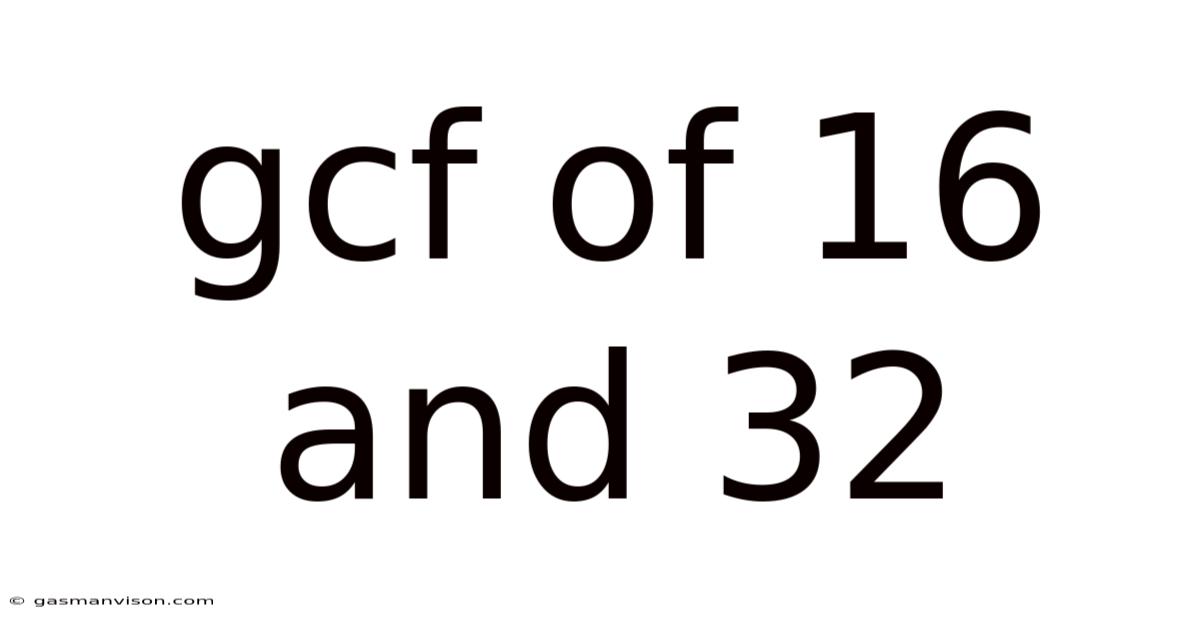
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 16 and 32: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and exploring different methods for calculating the GCF not only provides a solid foundation in number theory but also opens doors to more complex mathematical concepts. This article delves into the GCF of 16 and 32, demonstrating various approaches, explaining the underlying theory, and showcasing the practical applications of this fundamental concept.
Meta Description: Learn how to find the greatest common factor (GCF) of 16 and 32 using multiple methods. This comprehensive guide explains the concept, explores different techniques, and highlights the importance of GCF in mathematics and beyond.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
This seemingly basic concept forms the bedrock of various mathematical operations, including simplification of fractions, solving algebraic equations, and understanding modular arithmetic. Mastering the calculation of the GCF is crucial for progress in higher-level mathematics.
Method 1: Listing Factors
The most straightforward method for finding the GCF of relatively small numbers like 16 and 32 is to list all their factors and identify the largest common one.
Factors of 16: 1, 2, 4, 8, 16 Factors of 32: 1, 2, 4, 8, 16, 32
By comparing the two lists, we can clearly see that the common factors are 1, 2, 4, 8, and 16. The largest of these common factors is 16. Therefore, the GCF of 16 and 32 is 16.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. This method is particularly useful for larger numbers where listing all factors becomes cumbersome. Let's apply this to find the GCF of 16 and 32.
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2⁵
The GCF is found by identifying the common prime factors and taking the lowest power of each. In this case, both numbers only have 2 as a prime factor. The lowest power of 2 present in both factorizations is 2⁴ (which is 16). Therefore, the GCF of 16 and 32 is 16.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's illustrate this with 16 and 32:
- Start with the larger number (32) and the smaller number (16): 32 and 16
- Subtract the smaller number from the larger number: 32 - 16 = 16
- Replace the larger number with the result (16): 16 and 16
- Since the two numbers are now equal, the GCF is 16.
The Euclidean algorithm provides a systematic and efficient approach, particularly advantageous when dealing with significantly larger numbers where prime factorization might become computationally intensive.
Understanding the Relationship between LCM and GCF
The least common multiple (LCM) and the greatest common factor (GCF) are closely related concepts. For any two positive integers a and b, the product of their GCF and LCM is always equal to the product of the two numbers themselves. This relationship can be expressed as:
GCF(a, b) * LCM(a, b) = a * b
Using this relationship, if we know the GCF of 16 and 32 (which is 16), we can calculate the LCM:
GCF(16, 32) * LCM(16, 32) = 16 * 32 16 * LCM(16, 32) = 512 LCM(16, 32) = 512 / 16 LCM(16, 32) = 32
Applications of GCF in Real-World Scenarios
The concept of the GCF extends far beyond the realm of abstract mathematics. It has practical applications in various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For instance, the fraction 32/16 can be simplified to 2/1 by dividing both the numerator and denominator by their GCF, which is 16.
-
Dividing Objects into Equal Groups: Imagine you have 16 apples and 32 oranges, and you want to divide them into the largest possible equal groups without any leftovers. The GCF of 16 and 32 (16) tells you that you can create 16 groups, each containing one apple and two oranges.
-
Geometric Problems: GCF can be used to solve problems involving dimensions and areas. For example, determining the largest square tiles that can perfectly cover a rectangular floor with dimensions 16ft by 32ft.
-
Music Theory: The GCF is instrumental in understanding musical intervals and harmonies. Finding the GCF of two note frequencies helps determine the simplest ratio between them.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors with the lowest powers. For the Euclidean algorithm, you would apply it iteratively, first finding the GCF of two numbers and then using that result to find the GCF with the next number, and so on.
For example, let's find the GCF of 16, 32, and 48:
- Prime factorization:
- 16 = 2⁴
- 32 = 2⁵
- 48 = 2⁴ x 3
- The common prime factor is 2, and the lowest power is 2⁴. Therefore, the GCF(16, 32, 48) = 16.
Conclusion
Finding the greatest common factor (GCF) of 16 and 32, as demonstrated through various methods, underscores the fundamental importance of number theory in mathematics and its practical applications in diverse fields. Understanding the different approaches—listing factors, prime factorization, and the Euclidean algorithm—equips you with the tools to tackle more complex problems involving GCF and related concepts like LCM. By mastering these techniques, you’ll develop a strong foundation in mathematics and appreciate the elegance and practicality of seemingly simple arithmetic concepts. The GCF, seemingly a simple concept, is a cornerstone upon which much of higher-level mathematics is built.
Latest Posts
Latest Posts
-
60 Is 1 10 Of
Sep 12, 2025
-
If Joe Ran 390 Feet
Sep 12, 2025
-
Molecular Mass Of Aluminum Sulfate
Sep 12, 2025
-
Collaborate Teammate Synonym Or Antonym
Sep 12, 2025
-
What Are Young Penguins Called
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.