Gcf Of 35 And 63
gasmanvison
Sep 21, 2025 · 6 min read
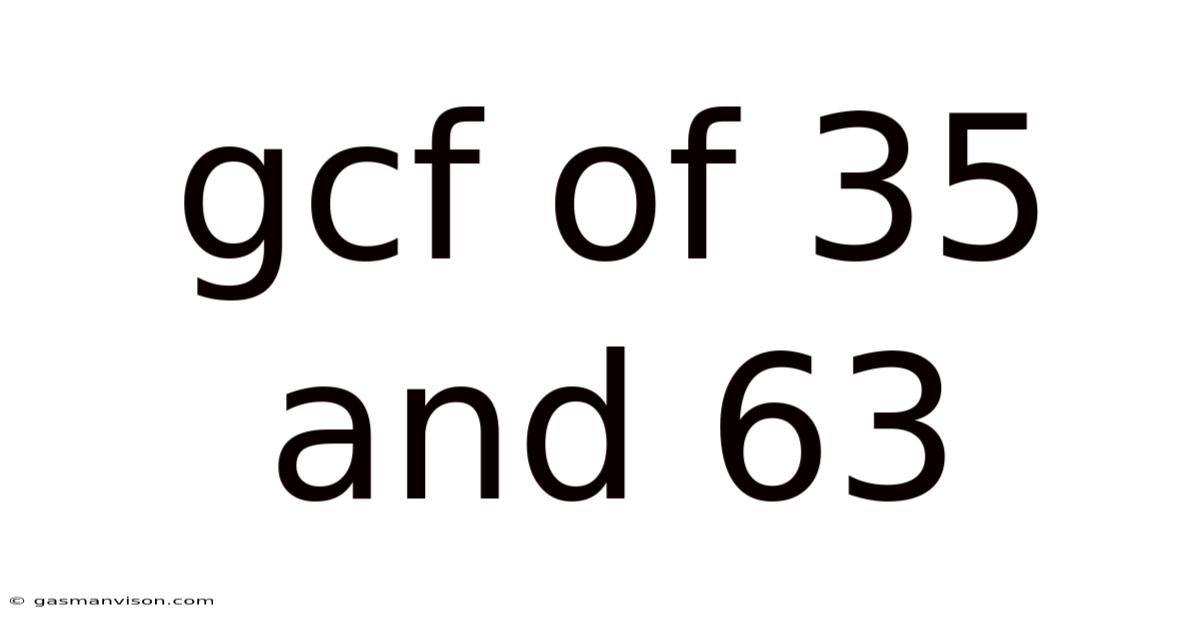
Table of Contents
Finding the Greatest Common Factor (GCF) of 35 and 63: A Comprehensive Guide
This article delves into the fascinating world of number theory, specifically focusing on how to determine the greatest common factor (GCF), also known as the greatest common divisor (GCD), of 35 and 63. We'll explore multiple methods, from elementary techniques suitable for beginners to more advanced approaches, providing a comprehensive understanding of this fundamental concept in mathematics. Understanding GCF is crucial not only for academic success but also for various applications in fields like computer science and cryptography. This in-depth guide will equip you with the knowledge and skills to confidently tackle GCF problems, regardless of the numbers involved.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Finding the GCF is a cornerstone of many mathematical operations and problem-solving techniques.
Methods for Finding the GCF of 35 and 63
Several methods can be used to find the GCF of 35 and 63. Let's explore the most common ones:
1. Listing Factors Method:
This method involves listing all the factors of each number and then identifying the largest factor common to both.
- Factors of 35: 1, 5, 7, 35
- Factors of 63: 1, 3, 7, 9, 21, 63
By comparing the two lists, we can see that the common factors are 1 and 7. The greatest of these common factors is 7. Therefore, the GCF of 35 and 63 is 7.
This method is straightforward for smaller numbers but becomes cumbersome and inefficient for larger numbers with many factors.
2. Prime Factorization Method:
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
- Prime factorization of 35: 5 x 7
- Prime factorization of 63: 3 x 3 x 7 (or 3² x 7)
To find the GCF, we identify the common prime factors and multiply them together. Both 35 and 63 share the prime factor 7. Therefore, the GCF of 35 and 63 is 7.
This method is more efficient than the listing factors method, especially when dealing with larger numbers. It provides a systematic approach to finding the GCF, regardless of the size of the numbers.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 35 and 63:
- 63 = 1 x 35 + 28 (Subtract 35 from 63, the remainder is 28)
- 35 = 1 x 28 + 7 (Subtract 28 from 35, the remainder is 7)
- 28 = 4 x 7 + 0 (Subtract multiples of 7 from 28 until the remainder is 0)
The last non-zero remainder is 7, which is the GCF of 35 and 63.
The Euclidean algorithm is particularly useful for finding the GCF of larger numbers because it avoids the need to find all factors. It's a highly efficient and elegant method widely used in computer science for its computational efficiency.
Applications of Finding the Greatest Common Factor
Understanding and applying the GCF has various real-world applications:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For instance, the fraction 35/63 can be simplified to 5/9 by dividing both the numerator and denominator by their GCF, which is 7.
-
Solving Word Problems: Many word problems involving division and sharing require finding the GCF to determine the largest possible equal groups or shares. For example, if you have 35 apples and 63 oranges, and you want to divide them into equal-sized bags with the same number of apples and oranges in each bag, the GCF (7) will determine the maximum number of bags you can make. Each bag will contain 5 apples and 9 oranges.
-
Geometry: GCF finds applications in geometry problems related to finding the dimensions of squares or rectangles that can be formed from a given area or perimeter.
-
Computer Science and Cryptography: The Euclidean algorithm, which is used to find the GCF, plays a vital role in various cryptographic algorithms and computer science applications, particularly in RSA encryption. It's used for tasks such as key generation and modular arithmetic computations.
-
Music Theory: GCF is used in music theory to find the greatest common divisor of the number of beats in a measure and the number of beats in a phrase, allowing for the accurate determination of rhythmic relationships and patterns.
-
Data Analysis: GCF can help in data analysis by finding the common factors in datasets, facilitating better organization and analysis.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 35, 63, and 105:
-
Prime Factorization Method:
- Prime factorization of 35: 5 x 7
- Prime factorization of 63: 3² x 7
- Prime factorization of 105: 3 x 5 x 7
The common prime factors are 7. Therefore, the GCF of 35, 63, and 105 is 7.
-
Euclidean Algorithm Extension: While the standard Euclidean algorithm is for two numbers, you can extend it by repeatedly finding the GCF of two numbers at a time. First, find the GCF of 35 and 63 (which is 7). Then, find the GCF of 7 and 105 (which is 7). Therefore, the GCF of 35, 63, and 105 is 7.
Conclusion:
Finding the greatest common factor (GCF) is a fundamental concept in number theory with diverse applications across various fields. This comprehensive guide has explored different methods for determining the GCF, focusing particularly on the numbers 35 and 63, demonstrating the efficiency and versatility of each technique. From the straightforward listing factors method to the highly efficient Euclidean algorithm, the choice of method depends on the complexity and size of the numbers involved. Understanding these methods empowers you to tackle GCF problems confidently and appreciate the significance of this mathematical concept in various practical contexts. Mastering the GCF not only enhances your mathematical skills but also opens doors to understanding more advanced mathematical concepts and their applications in various disciplines. Remember to choose the method that best suits your needs and the complexity of the problem you are facing.
Latest Posts
Latest Posts
-
Whats 700 000 In Pennies
Sep 21, 2025
-
Startservice Failed With Error 4294967201
Sep 21, 2025
-
The Xyz Office Supplies Company
Sep 21, 2025
-
Batesian Mimicry Vs Mullerian Mimicry
Sep 21, 2025
-
Symbol Of The Legislative Branch
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 35 And 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.