Gcf Of 40 And 24
gasmanvison
Sep 09, 2025 · 5 min read
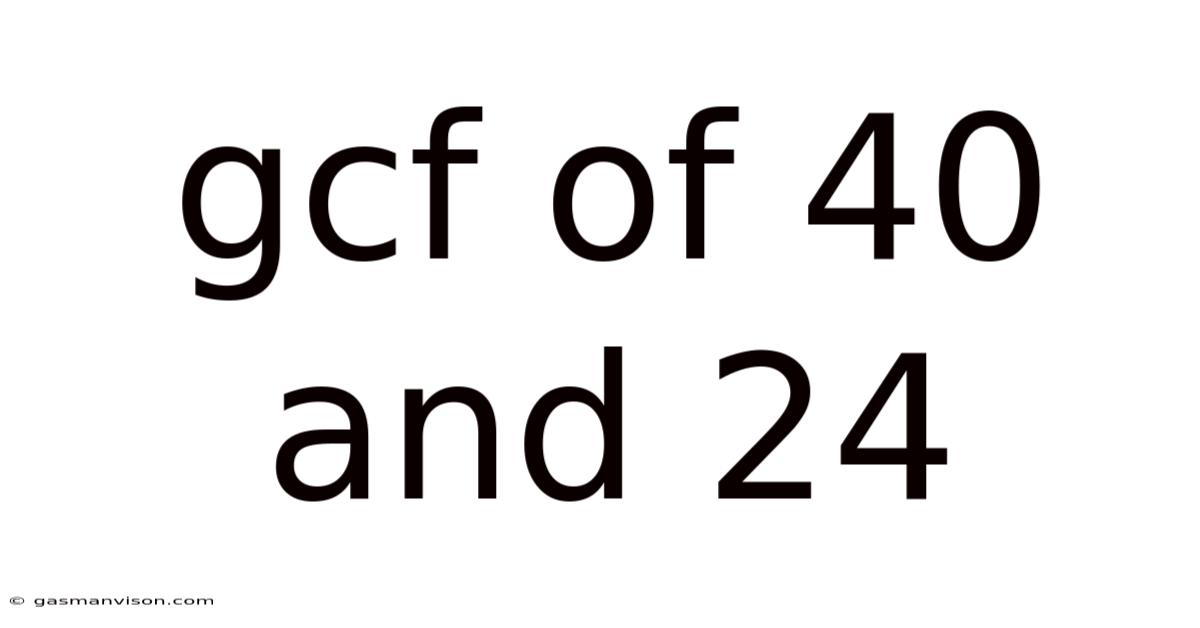
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 40 and 24: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications spanning various fields, from cryptography to computer science. This article will delve into the intricacies of determining the GCF of 40 and 24, exploring multiple methods and illustrating the underlying mathematical principles. We'll also touch upon the broader significance of GCFs and their practical uses.
Meta Description: Learn how to find the greatest common factor (GCF) of 40 and 24 using various methods, including prime factorization, the Euclidean algorithm, and listing factors. Discover the significance of GCFs in mathematics and their real-world applications.
Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and even in more advanced mathematical concepts. The GCF of two numbers is the largest number that divides both numbers without leaving a remainder. Let's explore how to find the GCF of 40 and 24 using several effective techniques.
Method 1: Prime Factorization
Prime factorization is a powerful technique for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
First, let's find the prime factorization of 40:
40 = 2 x 2 x 2 x 5 = 2³ x 5
Next, let's find the prime factorization of 24:
24 = 2 x 2 x 2 x 3 = 2³ x 3
Now, we identify the common prime factors and their lowest powers present in both factorizations. Both 40 and 24 share three factors of 2 (2³). There are no other common prime factors. Therefore, the GCF of 40 and 24 is 2³ = 8.
This method is particularly useful for understanding the fundamental structure of numbers and is a solid foundation for more advanced mathematical concepts. It's also relatively easy to understand and apply, making it ideal for beginners.
Method 2: Listing Factors
A more straightforward, though potentially less efficient for larger numbers, method involves listing all the factors of each number and identifying the greatest common factor.
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Comparing the two lists, we can see that the common factors are 1, 2, 4, and 8. The greatest of these common factors is 8. Therefore, the GCF of 40 and 24 is 8.
This method is intuitive and easy to visualize, but it can become cumbersome when dealing with larger numbers with numerous factors. It's a good method for smaller numbers, allowing for a clear visual representation of the factors.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 40 and 24:
- Step 1: 40 ÷ 24 = 1 with a remainder of 16.
- Step 2: 24 ÷ 16 = 1 with a remainder of 8.
- Step 3: 16 ÷ 8 = 2 with a remainder of 0.
The last non-zero remainder is 8, which is the GCF of 40 and 24. The Euclidean algorithm is significantly more efficient than listing factors, especially when dealing with large numbers. It's a fundamental algorithm in number theory and has numerous applications in computer science and cryptography.
Understanding the Significance of the GCF
The GCF has far-reaching implications across various mathematical and practical applications. Some key applications include:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 40/24 can be simplified by dividing both the numerator and denominator by their GCF, 8, resulting in the simplified fraction 5/3.
-
Solving Algebraic Equations: GCFs play a vital role in factoring algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and easier solving of equations.
-
Geometry and Measurement: GCFs are used in geometry when finding the dimensions of the largest square that can tile a rectangular area. For instance, if you have a rectangle with sides of 40 units and 24 units, the largest square that can perfectly tile this rectangle has sides of 8 units.
-
Cryptography: GCFs are fundamental to certain cryptographic algorithms, contributing to the security of data encryption and decryption processes. Understanding GCFs is crucial in fields like public-key cryptography.
-
Computer Science: The Euclidean algorithm, used for calculating the GCF, is a core algorithm in computer science, used in various applications, including modular arithmetic and cryptography. Its efficiency makes it highly valuable in optimizing computational processes.
Beyond the Basics: Extending the Concept
The concept of GCF extends beyond just two numbers. We can find the GCF of three or more numbers by applying the same principles. For example, to find the GCF of 40, 24, and 16, we could use prime factorization or the Euclidean algorithm iteratively. The prime factorization method would involve finding the prime factors of each number and identifying the common factors with the lowest power. The Euclidean algorithm could be applied repeatedly, finding the GCF of two numbers at a time.
Furthermore, the concept of GCF is closely related to the least common multiple (LCM). The LCM of two numbers is the smallest number that is a multiple of both numbers. There's a relationship between the GCF and LCM: The product of the GCF and LCM of two numbers is equal to the product of the two numbers. This relationship provides a useful shortcut for finding the LCM once the GCF is known.
Conclusion: Mastering the GCF
Understanding the greatest common factor is a cornerstone of number theory with practical applications across numerous fields. This article has explored three distinct methods for finding the GCF of 40 and 24: prime factorization, listing factors, and the Euclidean algorithm. We've also discussed the broader significance of the GCF, its use in simplifying fractions, solving equations, and its role in more advanced mathematical concepts and practical applications. Mastering the GCF not only enhances your mathematical skills but also provides a foundation for understanding more complex mathematical ideas and their applications in the real world. By understanding the underlying principles and applying the appropriate methods, you can confidently tackle GCF problems of varying complexity.
Latest Posts
Latest Posts
-
Greg Has 60 Building Blocks
Sep 09, 2025
-
Zane Is Mixing Fruit Punch
Sep 09, 2025
-
Which Phrase Best Describes Osorno
Sep 09, 2025
-
Are Peptide Bonds Ester Linkages
Sep 09, 2025
-
Faceing Math Lesson 7 Answers
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 40 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.