Gcf Of 48 And 72
gasmanvison
Sep 24, 2025 · 5 min read
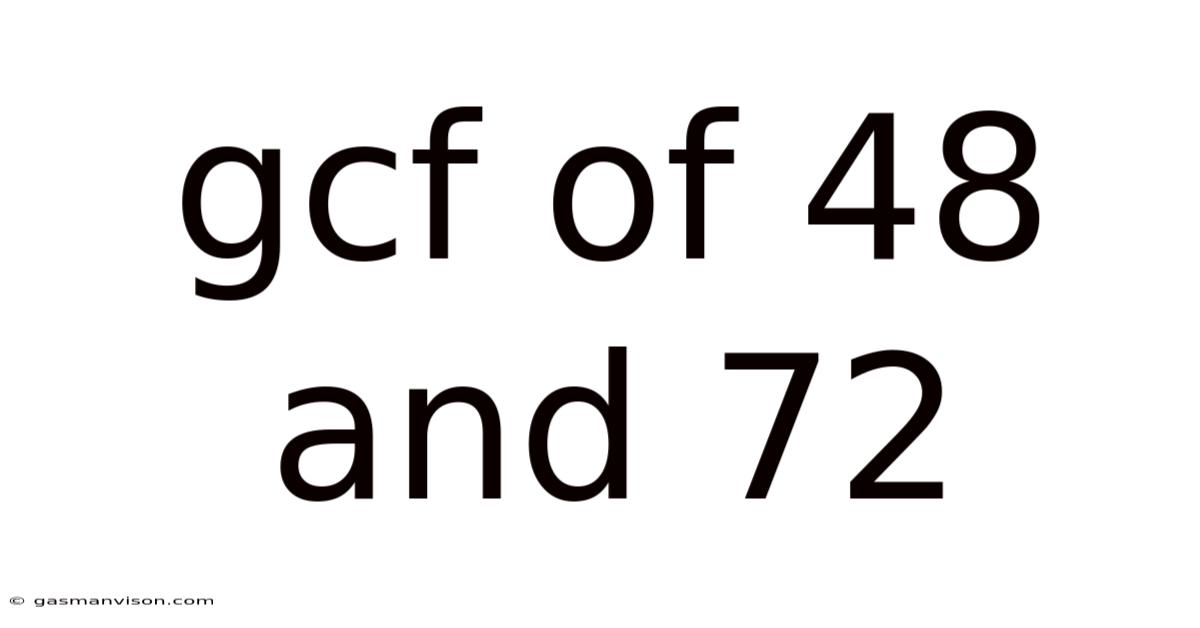
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 48 and 72: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications spanning various fields, from simplifying fractions to solving complex algebraic equations. This article provides a comprehensive exploration of how to determine the GCF of 48 and 72, employing several different methods, and expanding upon the underlying mathematical principles involved. Understanding these methods will empower you to efficiently calculate the GCF of any pair of numbers.
What is the Greatest Common Factor (GCF)?
Before delving into the specific calculation for 48 and 72, let's solidify our understanding of the GCF. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. It's essentially the largest number that's a common factor to all the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF(12, 18) = 6.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers, is to list all the factors of each number and then identify the largest common factor.
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Comparing the two lists, we can see that the common factors are 1, 2, 3, 4, 6, 8, 12, and 24. The greatest of these common factors is 24. Therefore, the GCF(48, 72) = 24.
This method is simple to understand but becomes less efficient as the numbers get larger. Finding all the factors of very large numbers can be time-consuming.
Method 2: Prime Factorization
Prime factorization is a more systematic and efficient method for finding the GCF, particularly for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- Prime factorization of 48: 2 x 2 x 2 x 2 x 3 = 2⁴ x 3¹
- Prime factorization of 72: 2 x 2 x 2 x 3 x 3 = 2³ x 3²
To find the GCF using prime factorization, we identify the common prime factors and take the lowest power of each. Both 48 and 72 share the prime factors 2 and 3.
- The lowest power of 2 is 2³ = 8
- The lowest power of 3 is 3¹ = 3
Multiplying these lowest powers together, we get: 8 x 3 = 24. Therefore, the GCF(48, 72) = 24.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 48 and 72:
- 72 ÷ 48 = 1 with a remainder of 24
- 48 ÷ 24 = 2 with a remainder of 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 24. Therefore, the GCF(48, 72) = 24. This method is particularly efficient for larger numbers because it avoids the need to find all factors.
Applications of the GCF
The GCF has numerous applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 48/72 can be simplified by dividing both the numerator and the denominator by their GCF (24), resulting in the equivalent fraction 2/3.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations whose solutions are restricted to integers. The GCF plays a significant role in determining the solvability and finding solutions to these equations.
-
Least Common Multiple (LCM): The GCF is closely related to the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. The relationship between the GCF and LCM is given by the formula: LCM(a, b) x GCF(a, b) = a x b. Knowing the GCF allows for easy calculation of the LCM.
-
Modular Arithmetic: The GCF is fundamental in modular arithmetic, which deals with remainders after division. Concepts like modular inverses and solving congruences rely heavily on the GCF.
-
Cryptography: Number theory, including the concept of GCF, forms the backbone of many modern cryptographic systems, ensuring secure communication and data protection.
Further Exploration of Number Theory Concepts
Understanding the GCF opens doors to exploring more advanced concepts in number theory:
-
Relatively Prime Numbers: Two numbers are relatively prime (or coprime) if their GCF is 1. This means they share no common factors other than 1.
-
Extended Euclidean Algorithm: This is an extension of the Euclidean algorithm that not only finds the GCF but also finds integers x and y such that ax + by = GCF(a, b). This has applications in cryptography and other areas.
-
Chinese Remainder Theorem: This theorem deals with solving systems of congruences and utilizes the concept of GCF in its solution.
Conclusion:
Finding the greatest common factor of 48 and 72, as demonstrated through various methods, is more than just a simple arithmetic exercise. It's a gateway to understanding fundamental principles in number theory with broad applications in mathematics, computer science, and cryptography. Mastering these methods equips you with valuable skills for solving more complex mathematical problems and appreciating the elegance and power of number theory. By understanding the different approaches—listing factors, prime factorization, and the Euclidean algorithm—you can choose the most efficient method depending on the size and complexity of the numbers involved. The GCF is not merely a mathematical concept; it’s a building block for more advanced mathematical structures and real-world applications.
Latest Posts
Latest Posts
-
2 1 2 Feet In Inches
Sep 24, 2025
-
How Long Is 5 Weeks
Sep 24, 2025
-
5 X 5 X 2
Sep 24, 2025
-
Which Sentence Describes Impressionist Paintings
Sep 24, 2025
-
Lewis Dot Structure Of Hocl
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 48 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.