Gcf Of 48 And 8
gasmanvison
Sep 20, 2025 · 5 min read
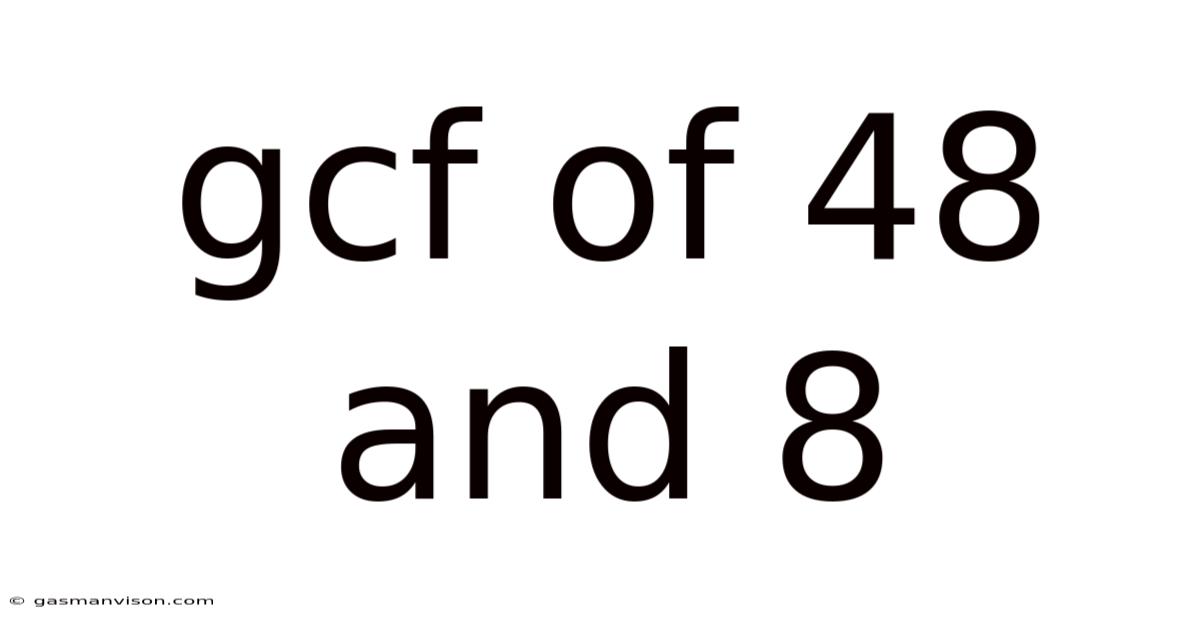
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 48 and 8: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This article delves into the process of determining the GCF of 48 and 8, exploring multiple methods, and highlighting the significance of this mathematical operation. We'll cover various techniques, from prime factorization to the Euclidean algorithm, providing a comprehensive understanding suitable for both beginners and those seeking a refresher. This in-depth explanation will also touch upon the practical applications of GCF in different fields, making it a valuable resource for students and enthusiasts alike.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Finding the GCF is a crucial skill in simplifying fractions, solving algebraic problems, and understanding number theory concepts.
Method 1: Prime Factorization
The prime factorization method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. This is arguably the most intuitive method for finding the GCF, especially for smaller numbers. Let's apply it to find the GCF of 48 and 8:
- Prime factorization of 48: 48 can be broken down as 2 x 2 x 2 x 2 x 3, or 2⁴ x 3.
- Prime factorization of 8: 8 can be expressed as 2 x 2 x 2, or 2³.
Now, identify the common prime factors and their lowest powers:
Both 48 and 8 share three factors of 2 (2³). Therefore, the GCF of 48 and 8 is 2³.
2³ = 8
Therefore, the GCF of 48 and 8 is 8.
Method 2: Listing Factors
This method is straightforward, particularly useful for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
- Factors of 8: 1, 2, 4, 8
Comparing the two lists, we can see that the common factors are 1, 2, 4, and 8. The largest of these common factors is 8. Therefore, the GCF of 48 and 8 is 8.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. This method is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 48 and 8:
- Divide the larger number (48) by the smaller number (8): 48 ÷ 8 = 6 with a remainder of 0.
Since the remainder is 0, the smaller number (8) is the GCF.
Therefore, the GCF of 48 and 8 is 8.
Method 4: Using the Division Algorithm
The division algorithm states that for any two integers 'a' and 'b', where b ≠ 0, there exist unique integers 'q' and 'r' such that a = bq + r, where 0 ≤ r < |b|. This method uses successive division until the remainder becomes zero. The last non-zero remainder is the GCF.
Let's find the GCF of 48 and 8:
- Divide 48 by 8: 48 = 8 * 6 + 0
The remainder is 0, so the GCF is the divisor, which is 8.
Why is Finding the GCF Important?
The GCF has several crucial applications in various mathematical and real-world contexts:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For instance, the fraction 48/8 can be simplified by dividing both the numerator and the denominator by their GCF (8), resulting in the simplified fraction 6/1 or simply 6.
-
Solving Algebraic Equations: GCF plays a role in factoring polynomials and simplifying algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and easier manipulation of the equation.
-
Number Theory: GCF is a fundamental concept in number theory, used in various theorems and proofs related to prime numbers, divisibility, and modular arithmetic.
-
Real-World Applications: GCF finds applications in areas such as:
- Geometry: Determining the dimensions of squares or rectangles with the largest possible sides from given areas.
- Measurement: Converting measurements to simpler units by finding common factors.
- Resource Allocation: Dividing resources (e.g., sweets among children) fairly.
Further Exploration: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors with the lowest powers. For the Euclidean algorithm, you would find the GCF of two numbers, and then find the GCF of the result and the next number, repeating the process until all numbers are considered.
For example, to find the GCF of 48, 8, and 16:
- Prime factorization of 48: 2⁴ x 3
- Prime factorization of 8: 2³
- Prime factorization of 16: 2⁴
The common prime factor is 2, and the lowest power is 2³. Therefore, the GCF of 48, 8, and 16 is 8.
Conclusion:
Determining the greatest common factor is a cornerstone of number theory and has far-reaching implications in various fields. This article has explored multiple methods – prime factorization, listing factors, the Euclidean algorithm, and the division algorithm – to calculate the GCF, demonstrating their effectiveness in different situations. Understanding these methods provides a solid foundation for tackling more complex mathematical problems and appreciating the elegance and power of fundamental mathematical concepts. The simplicity of finding the GCF of 48 and 8 belies the depth and breadth of its applications across numerous mathematical domains and real-world scenarios. The ability to efficiently calculate the GCF is a valuable skill for students and anyone working with numbers.
Latest Posts
Latest Posts
-
30ml Is How Many Ounces
Sep 20, 2025
-
Who Defines Lumber Inspection Criteria
Sep 20, 2025
-
11 1 0 01 0 11 0 111
Sep 20, 2025
-
Which Characteristic Describes The Troposphere
Sep 20, 2025
-
Spell Deer Without A D
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 48 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.