Graph Y 1 2f X
gasmanvison
Sep 14, 2025 · 6 min read
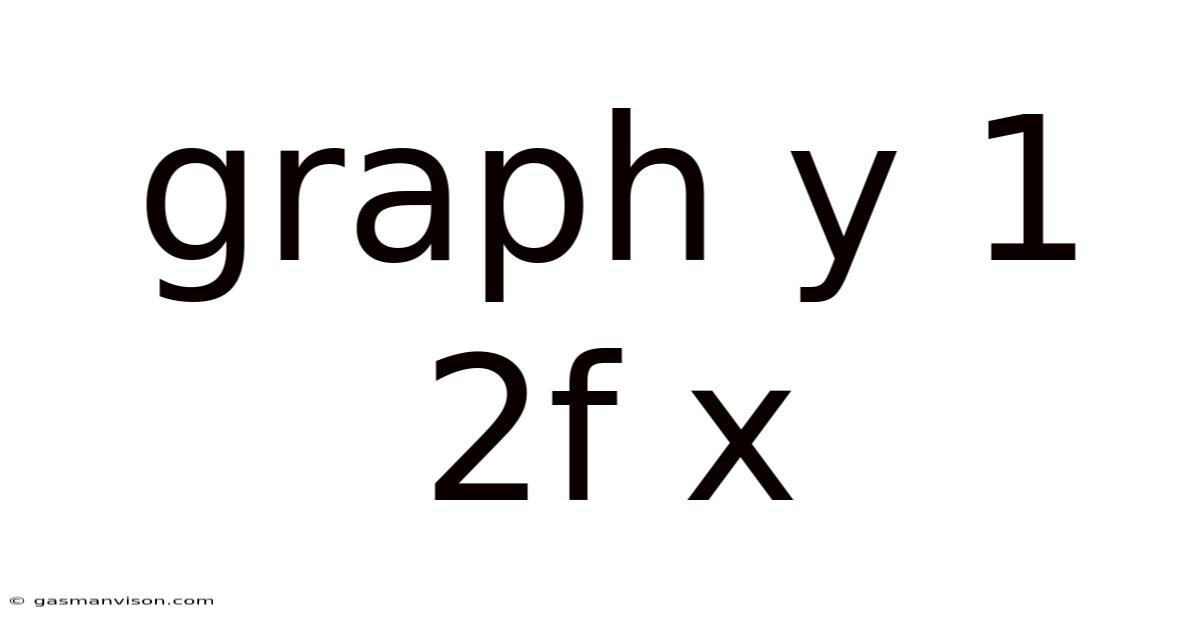
Table of Contents
Decoding the Graph of y = 1/(2f(x)): A Comprehensive Guide
This article delves into the intricacies of graphing the function y = 1/(2f(x)), exploring its transformations, asymptotes, and behavior relative to the parent function f(x). We'll examine how changes to f(x) affect the graph of y, providing a comprehensive understanding for students and anyone interested in function transformations and graph analysis. Understanding this transformation is key to mastering more complex function manipulations and problem-solving in calculus and related fields.
Understanding the Parent Function f(x)
Before diving into the intricacies of y = 1/(2f(x)), it's crucial to have a solid grasp of the parent function, f(x). The nature of f(x) – whether it's linear, quadratic, polynomial, exponential, trigonometric, or otherwise – significantly dictates the characteristics of the transformed function. The behavior of f(x), including its intercepts, asymptotes, and overall shape, directly influences the resulting graph of y = 1/(2f(x)). For example, the zeros of f(x) will become vertical asymptotes in the transformed function, while the horizontal asymptote of f(x) will be affected by the scaling factor.
The Transformation: 1/(2f(x))
The expression y = 1/(2f(x)) involves two key transformations applied to the original function f(x):
-
Multiplication by 1/2: This represents a vertical compression (or shrinking) of the function f(x) by a factor of 1/2. Every y-coordinate of f(x) is halved. This scaling affects the amplitude and overall vertical extent of the graph.
-
Reciprocal Function: The entire compressed function (1/2 * f(x)) is then subjected to a reciprocal transformation (1/x). This is where the most significant changes occur.
Analyzing the Effects of the Reciprocal Transformation (1/x)
The reciprocal transformation, 1/x, is a powerful operation that drastically alters the graph's characteristics. Here's a breakdown of its key effects:
-
Vertical Asymptotes: Wherever f(x) = 0 (the x-intercepts of the original function), the transformed function y = 1/(2f(x)) will have vertical asymptotes. This is because division by zero is undefined. These asymptotes are vertical lines at the x-coordinates where f(x) crosses the x-axis.
-
Horizontal Asymptote: If f(x) approaches 0 as x approaches infinity (or negative infinity), then y = 1/(2f(x)) will have a horizontal asymptote at y = 0. This is because as the denominator gets very large, the fraction approaches zero. Conversely, if f(x) approaches a non-zero value as x approaches infinity (or negative infinity), then y = 1/(2f(x)) will have a horizontal asymptote at y = 1/(2 * (limit of f(x) as x approaches infinity)).
-
Sign Changes: The sign of f(x) dictates the sign of y. If f(x) is positive, y will be positive. If f(x) is negative, y will be negative. This leads to sections of the graph being above or below the x-axis, reflecting the sign changes in f(x).
-
Behavior Around Asymptotes: The graph will approach the vertical asymptotes either from positive infinity or negative infinity, depending on whether f(x) approaches 0 from positive or negative values. Similarly, the approach to the horizontal asymptote will depend on the long-term behavior of f(x).
-
Symmetry: If f(x) exhibits certain symmetries (even or odd), these symmetries might be preserved or altered in the transformed function. Careful analysis is needed to determine how the reciprocal and scaling transformations affect the symmetry of the original function.
Illustrative Examples:
Let's examine several cases to solidify our understanding:
Example 1: f(x) = x
If f(x) = x, then y = 1/(2x). This is a simple reciprocal function with a vertical asymptote at x = 0 and a horizontal asymptote at y = 0. The graph will be in the first and third quadrants.
Example 2: f(x) = x²
If f(x) = x², then y = 1/(2x²). This graph will resemble the previous example but will be entirely above the x-axis, since 2x² is always positive. Again, a vertical asymptote exists at x = 0, and a horizontal asymptote at y = 0.
Example 3: f(x) = x - 1
If f(x) = x - 1, then y = 1/(2(x-1)). This function has a vertical asymptote at x = 1 and a horizontal asymptote at y = 0. The graph will be similar to 1/(2x), but shifted one unit to the right.
Example 4: f(x) = sin(x)
If f(x) = sin(x), then y = 1/(2sin(x)). This becomes considerably more complex. Vertical asymptotes occur at every x where sin(x) = 0 (i.e., at multiples of π). The graph will exhibit periodic vertical asymptotes, and its behavior around these asymptotes will oscillate between positive and negative infinity. There is no horizontal asymptote in the traditional sense; the function oscillates infinitely.
Example 5: f(x) = e^x
If f(x) = e^x, then y = 1/(2e^x). There are no vertical asymptotes since e^x is always positive. However, there's a horizontal asymptote at y = 0 because as x approaches negative infinity, e^x approaches 0, making 1/(2e^x) approach infinity. Conversely, as x approaches positive infinity, 1/(2e^x) approaches 0.
Advanced Considerations:
-
Domain and Range: Carefully determine the domain and range of both f(x) and y = 1/(2f(x)). The domain of the transformed function will exclude the values of x where f(x) = 0. The range will depend on the behavior of f(x) and the reciprocal transformation.
-
Derivatives and Calculus: For those familiar with calculus, analyzing the derivatives of y = 1/(2f(x)) can provide further insight into its behavior, such as identifying local maxima, minima, and points of inflection. The derivative will involve the chain rule and the quotient rule.
-
Numerical Methods: In cases where the analysis becomes too complex, numerical methods (like plotting points or using graphing software) can be used to visualize the graph accurately.
Conclusion:
The transformation y = 1/(2f(x)) introduces a combination of scaling and reciprocal operations, leading to a potentially dramatic change in the graph compared to the parent function f(x). Understanding the effects of the reciprocal transformation, specifically the creation of vertical asymptotes and alterations to horizontal asymptotes, is key to sketching and analyzing this type of function. By systematically considering the characteristics of f(x) and applying the rules of transformations, one can effectively visualize and interpret the graph of y = 1/(2f(x)) for a wide range of parent functions. Remember to always analyze the zeros of f(x) to identify vertical asymptotes, and the behavior of f(x) as x approaches infinity to determine horizontal asymptotes. This detailed understanding forms a crucial foundation for more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
Label The Stages Of Mitosis
Sep 14, 2025
-
Which Illustration Depicts Homologous Chromosomes
Sep 14, 2025
-
How Many Oz In 375ml
Sep 14, 2025
-
Auto Insurance Is Needed Primarily
Sep 14, 2025
-
Amplify Supply Drop Best Design
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Graph Y 1 2f X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.