Graph Y 1 2x 2
gasmanvison
Sep 12, 2025 · 5 min read
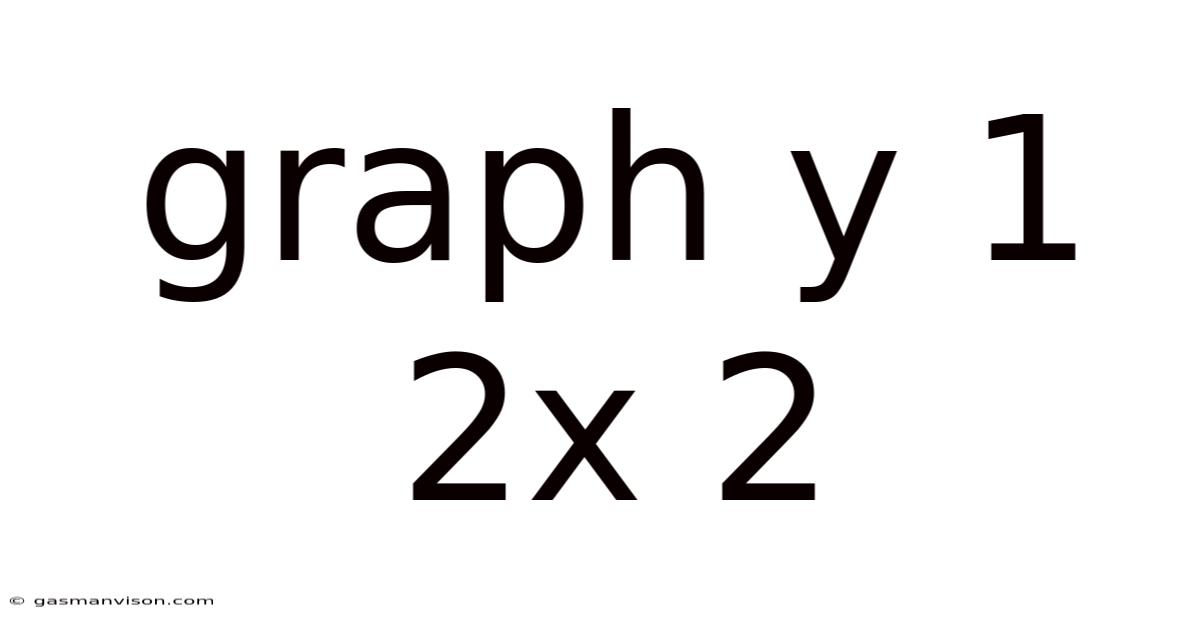
Table of Contents
A Deep Dive into the Linear Equation: y = 1/2x + 2
This article provides a comprehensive exploration of the linear equation y = 1/2x + 2, covering its graphical representation, key characteristics, applications, and related concepts. We'll delve into the slope-intercept form, finding x and y-intercepts, determining the slope, and analyzing its behavior in relation to other linear equations. Understanding this seemingly simple equation unlocks a wealth of knowledge in algebra and its practical applications.
Meta Description: Unlock the secrets of the linear equation y = 1/2x + 2. This in-depth guide covers its graph, slope, intercepts, practical applications, and how it relates to other linear equations. Learn to visualize and understand this fundamental concept in algebra.
Understanding the Slope-Intercept Form: y = mx + b
The equation y = 1/2x + 2 is written in the slope-intercept form, a standard way to represent linear equations. In this form:
- y represents the dependent variable (the output).
- x represents the independent variable (the input).
- m represents the slope of the line (the rate of change of y with respect to x).
- b represents the y-intercept (the point where the line crosses the y-axis, where x = 0).
In our equation, y = 1/2x + 2, the slope (m) is 1/2, and the y-intercept (b) is 2. This tells us a lot about the line's characteristics before we even graph it.
Graphing the Equation y = 1/2x + 2
To graph this equation, we can use two primary methods:
1. Using the Slope and Y-intercept:
- Y-intercept: The y-intercept is 2, meaning the line passes through the point (0, 2). Plot this point on your coordinate plane.
- Slope: The slope is 1/2, which can be interpreted as "rise over run." This means for every 2 units you move horizontally (run) along the x-axis, you move 1 unit vertically (rise) along the y-axis. Starting from the y-intercept (0, 2), move 2 units to the right and 1 unit up to find another point on the line (2, 3). You can repeat this process to find more points or move in the opposite direction (2 units left and 1 unit down) to find the point (-2, 1).
Once you have at least two points, draw a straight line passing through them. This line represents the graph of y = 1/2x + 2.
2. Using a Table of Values:
Create a table of x and y values that satisfy the equation:
| x | y = 1/2x + 2 |
|---|---|
| -4 | 0 |
| -2 | 1 |
| 0 | 2 |
| 2 | 3 |
| 4 | 4 |
Plot these points on the coordinate plane and draw a straight line through them. This will produce the same graph as the slope-intercept method.
Finding the X-intercept
The x-intercept is the point where the line crosses the x-axis (where y = 0). To find it, set y = 0 in the equation and solve for x:
0 = 1/2x + 2
-2 = 1/2x
x = -4
Therefore, the x-intercept is (-4, 0).
Analyzing the Slope
The slope of 1/2 indicates a positive correlation between x and y. As x increases, y also increases. The magnitude of the slope (1/2) indicates the steepness of the line. A slope of 1/2 means the line is relatively gentle; it's not as steep as a line with a slope of 2, for example.
Comparing with Other Linear Equations
Let's compare y = 1/2x + 2 with other linear equations to highlight its characteristics:
- y = x + 2: This line has a slope of 1, meaning it's steeper than y = 1/2x + 2. Both lines have the same y-intercept.
- y = 1/2x - 1: This line has the same slope as y = 1/2x + 2 but a different y-intercept (-1). The lines are parallel because they have the same slope.
- y = -2x + 2: This line has the same y-intercept but a negative slope (-2), indicating a negative correlation between x and y. The lines intersect at the y-intercept.
These comparisons illustrate how the slope and y-intercept influence the position and orientation of the line on the coordinate plane.
Applications of Linear Equations
Linear equations like y = 1/2x + 2 have numerous applications in various fields:
- Physics: Describing motion with constant velocity (where slope represents velocity and y-intercept represents initial position).
- Economics: Modeling linear relationships between variables like price and quantity demanded.
- Finance: Calculating simple interest, where the slope represents the interest rate.
- Engineering: Modeling linear relationships between physical quantities.
- Computer Science: Representing data relationships in algorithms and data structures.
Understanding linear equations is crucial for solving real-world problems involving linear relationships.
Advanced Concepts and Extensions
The understanding of y = 1/2x + 2 can be extended to more complex concepts:
- Systems of Linear Equations: Solving for multiple variables by considering multiple linear equations simultaneously.
- Linear Inequalities: Exploring regions on the coordinate plane defined by inequalities involving linear expressions.
- Linear Programming: Optimizing linear objective functions subject to linear constraints.
- Calculus: Understanding the slope as the derivative of a linear function and its role in finding tangents and rates of change.
Conclusion
The seemingly simple linear equation y = 1/2x + 2 serves as a foundational concept in algebra and mathematics, with broad applications across various disciplines. By understanding its slope-intercept form, graphing techniques, and relationships with other linear equations, we can effectively visualize, interpret, and utilize this powerful tool to solve problems and model real-world phenomena. Its study lays the groundwork for understanding more advanced mathematical concepts and their real-world implications. Mastering this equation provides a strong basis for tackling more complex mathematical challenges and opens doors to a deeper understanding of quantitative relationships. From simple graphical representation to its applications in diverse fields, y = 1/2x + 2 offers a gateway to the world of linear algebra and its practical power. Continue exploring and expanding your knowledge of this crucial mathematical concept!
Latest Posts
Latest Posts
-
Still Wines Are Those With
Sep 12, 2025
-
7 Pounds How Many Ounces
Sep 12, 2025
-
2 Quarts How Many Ounces
Sep 12, 2025
-
3 Components Of American System
Sep 12, 2025
-
Ca3 Po4 2 Molar Mass
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Graph Y 1 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.