Half Of 1 2 3
gasmanvison
Sep 08, 2025 · 5 min read
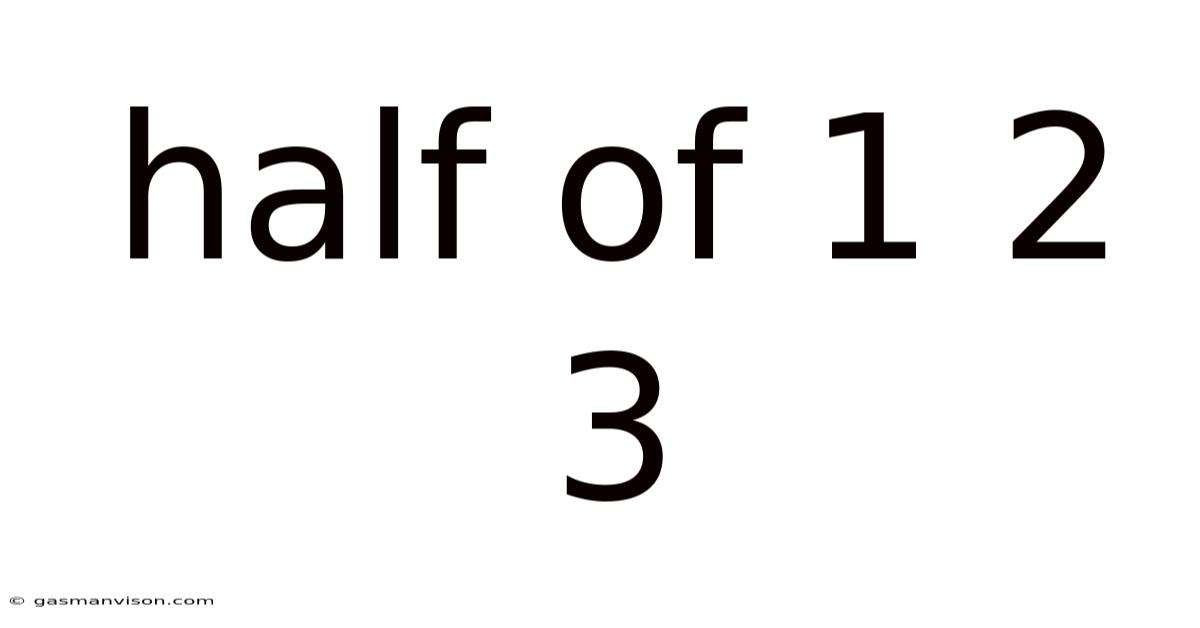
Table of Contents
Decoding "Half of 1, 2, 3": A Deep Dive into Fractions, Number Sense, and Problem-Solving
This seemingly simple phrase, "half of 1, 2, 3," opens a door to a fascinating exploration of mathematical concepts, problem-solving strategies, and the development of number sense. At its core, it's a basic fractions problem, but its implications extend far beyond elementary arithmetic. This article will dissect the problem, explore its variations, and delve into the pedagogical significance of understanding such seemingly simple concepts. We'll also consider its application in real-world scenarios and how it can be used to build stronger mathematical foundations.
What is "Half of 1, 2, 3"? A Simple Start
The most straightforward interpretation of "half of 1, 2, 3" involves finding half of each number individually. This leads to a simple set of answers:
- Half of 1: 1/2 or 0.5
- Half of 2: 2/2 = 1
- Half of 3: 3/2 or 1.5
This is the immediate and most commonly expected answer. However, the ambiguity inherent in the phrasing allows for a more nuanced exploration of mathematical thinking and problem-solving.
Beyond the Obvious: Exploring Ambiguity and Interpretation
The phrase's lack of explicit mathematical symbols allows for alternative interpretations. For instance, one could interpret it as finding half of the sum of 1, 2, and 3. In this case:
- Sum of 1, 2, and 3: 1 + 2 + 3 = 6
- Half of the sum: 6/2 = 3
This demonstrates how seemingly simple word problems can have multiple valid interpretations, emphasizing the importance of precise language and careful reading comprehension in mathematics. This ambiguity provides a valuable opportunity to discuss the importance of clarity in communication, a skill crucial not only in mathematics but also in many other fields.
Expanding the Concept: Fractions and Number Sense
Understanding "half of 1, 2, 3" directly relates to understanding fractions – a fundamental concept in mathematics. This problem serves as an excellent tool for developing number sense, which encompasses the intuitive understanding of numbers, their relationships, and their magnitudes. It allows for:
- Visual Representation: Using diagrams, manipulatives (like fraction circles or bars), or even simple drawings can help visualize what half of each number represents. This concrete representation strengthens understanding and makes the abstract concept more accessible.
- Decimal Equivalents: Converting fractions to decimals (1/2 = 0.5, 3/2 = 1.5) reinforces the connection between different number representations and strengthens computational skills.
- Comparison and Ordering: Comparing the results (0.5, 1, 1.5) allows for practice in ordering numbers and understanding their relative magnitudes.
Real-World Applications: Making it Relevant
While seemingly abstract, the concept of "half of 1, 2, 3" has numerous real-world applications:
- Sharing: Dividing items equally among people. For example, sharing three cookies among two friends involves finding half of three (1.5 cookies each).
- Measurement: Measuring ingredients in recipes, cutting materials to specific lengths, or calculating distances often involves working with fractions and halves.
- Data Analysis: In simpler data sets, understanding proportions and calculating averages involves similar calculations.
- Money Management: Splitting bills, calculating discounts, or understanding portions of a budget frequently requires fractional calculations.
Extending the Challenge: Variations and Extensions
The problem can be expanded in several ways to challenge students at different levels:
- Different Fractions: Instead of "half," use other fractions like "one-third," "one-quarter," or "two-thirds" to increase complexity. This introduces more challenging fraction calculations.
- Larger Numbers: Using larger numbers increases the complexity of the calculations and provides more opportunities to practice arithmetic skills.
- Combining Operations: Incorporate addition, subtraction, multiplication, or a combination of operations to create more complex multi-step problems. For example: "Find half of the sum of 1, 2, and 3, then add 2."
- Algebraic Representation: Introduce algebraic notation to represent the problem. For instance, let x represent "half of," and write the problem as x(1) + x(2) + x(3). This bridges the gap between arithmetic and algebra.
Pedagogical Implications: Teaching for Understanding
Teaching the concept of "half of 1, 2, 3" effectively involves more than simply providing the answers. It's about fostering:
- Conceptual Understanding: Focus on the meaning of fractions and their visual representation rather than just rote memorization of procedures.
- Problem-Solving Skills: Encourage students to explore different approaches and interpretations, fostering critical thinking and problem-solving abilities.
- Number Sense Development: Use various activities and representations to build students' intuition about numbers and their relationships.
- Communication Skills: Encourage students to articulate their thinking processes and explain their solutions clearly and concisely.
Beyond the Numbers: Cultivating Mathematical Thinking
The simple phrase "half of 1, 2, 3" provides a valuable springboard for developing crucial mathematical thinking skills. It's not just about getting the right answer but about:
- Understanding the Problem: Carefully reading and interpreting the question, identifying keywords, and understanding what's being asked.
- Developing a Strategy: Choosing appropriate methods and strategies to solve the problem. This might involve drawing diagrams, using manipulatives, or breaking the problem down into smaller, more manageable steps.
- Executing the Strategy: Accurately performing the calculations involved.
- Evaluating the Solution: Checking the answer for reasonableness and accuracy. Does it make sense in the context of the problem?
Conclusion: The Power of Simplicity
While seemingly trivial, the phrase "half of 1, 2, 3" offers a powerful tool for teaching fundamental mathematical concepts and developing crucial problem-solving skills. By exploring its various interpretations and extending the challenge, educators can create engaging learning experiences that foster a deeper understanding of fractions, number sense, and the process of mathematical thinking itself. The true value lies not solely in the numerical answers, but in the journey of exploration, interpretation, and application that this seemingly simple phrase facilitates. It serves as a microcosm of the broader mathematical landscape, showcasing the power of critical thinking, precise communication, and a deep understanding of foundational concepts. This seemingly simple phrase underscores the importance of questioning, exploring, and embracing the multifaceted nature of even the most basic mathematical problems. By fostering these skills, we empower students to approach more complex mathematical challenges with confidence and creativity.
Latest Posts
Latest Posts
-
Kg In Pounds And Stones
Sep 08, 2025
-
3 Quarts In A Gallon
Sep 08, 2025
-
Kwl Is An Example Of
Sep 08, 2025
-
Clearances Are Based Primarily On
Sep 08, 2025
-
Is 0 02 Less Than 0 05
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.