Half Of 2 2 3
gasmanvison
Sep 08, 2025 · 4 min read
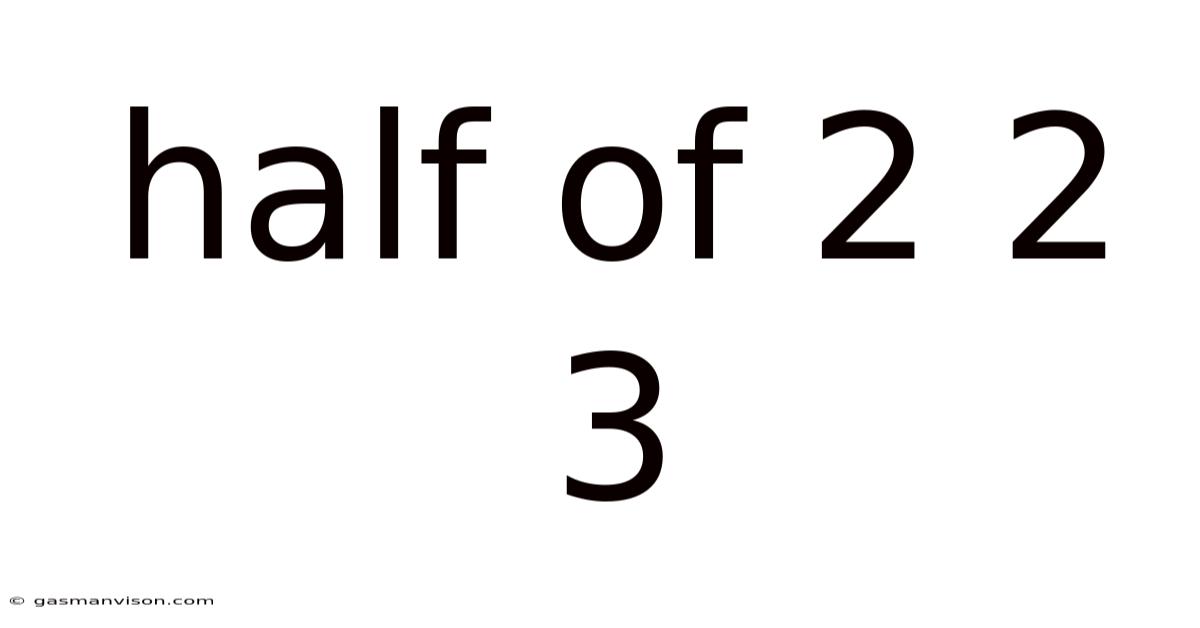
Table of Contents
Decoding "Half of 2, 2, 3": Exploring Mathematical Ambiguity and Problem-Solving Strategies
What does "half of 2, 2, 3" actually mean? At first glance, this seemingly simple phrase presents a mathematical puzzle, ripe with ambiguity and multiple potential interpretations. This article will delve into the various ways we can approach this problem, showcasing different mathematical concepts and problem-solving strategies. Understanding this seemingly simple phrase requires a nuanced understanding of mathematical operations, order of operations, and the importance of clear communication. Let's unravel this enigma together.
Understanding the Ambiguity: The Core of the Problem
The primary challenge with "half of 2, 2, 3" lies in its inherent ambiguity. The phrase lacks explicit mathematical symbols, relying instead on the reader's interpretation of natural language. This absence of precise notation opens the door to multiple valid interpretations, each leading to a different numerical result.
The ambiguity stems from the following points:
- "Half of": Does this refer to taking half of each number individually (2, 2, and 3), or taking half of the result of some operation performed on 2, 2, and 3?
- The commas: Do the commas imply separate entities, or do they indicate a grouping or sequence of numbers?
- The lack of operational symbols: Are we to assume addition, multiplication, or some other mathematical function between the numbers?
These ambiguities highlight the critical role of precise mathematical notation in avoiding confusion and ensuring unambiguous interpretation. Even a simple phrase can harbor multiple meanings without clear mathematical symbols.
Possible Interpretations and Solutions
Let's explore some of the most plausible interpretations and their corresponding solutions:
1. Half of each number individually:
This interpretation is the most straightforward. We simply take half of each number:
- Half of 2 = 1
- Half of 2 = 1
- Half of 3 = 1.5
This approach results in the sequence: 1, 1, 1.5.
2. Half of the sum:
Another plausible interpretation involves finding the sum of the numbers and then taking half of the result:
- 2 + 2 + 3 = 7
- Half of 7 = 3.5
This interpretation yields a single result: 3.5.
3. Half of the product:
This interpretation involves finding the product of the numbers and then taking half of the result:
- 2 * 2 * 3 = 12
- Half of 12 = 6
This approach results in a single answer: 6.
4. Half of a weighted average:
We could consider assigning weights to the numbers and calculating a weighted average, then taking half of the result. This would require additional information or assumptions about the weights assigned to each number. Without such information, this interpretation remains speculative.
5. Considering other operations:
Depending on context or additional information, other mathematical operations could be considered. For example:
- Geometric Mean: The geometric mean of 2, 2, and 3 is approximately 2.29. Half of this would be approximately 1.145.
- Median: The median of the numbers 2, 2, and 3 is 2. Half of the median would be 1.
The Importance of Context and Clear Communication
The multiple interpretations highlight the crucial role of context and clear communication in mathematics. The phrase "half of 2, 2, 3" is inherently ambiguous without further clarification. In real-world applications, especially in fields like engineering, finance, and programming, precise mathematical notation is paramount to avoid errors and ensure accurate results.
Applying Problem-Solving Strategies:
This seemingly simple problem provides an excellent opportunity to illustrate various problem-solving strategies:
- Breaking Down the Problem: We systematically broke down the phrase into its constituent parts to identify potential ambiguities and explore different interpretations.
- Identifying Assumptions: We explicitly stated the assumptions underlying each interpretation, making the reasoning transparent and allowing for critical evaluation.
- Systematic Exploration: We explored multiple potential interpretations rather than settling on the first idea that came to mind.
- Considering Different Mathematical Concepts: We applied a range of mathematical concepts, including addition, multiplication, weighted averages, geometric means, and medians, demonstrating the versatility of mathematical tools.
- Evaluating Solutions: We presented the solutions for each interpretation, clearly indicating the reasoning behind each result.
Beyond the Numbers: Lessons Learned
The ambiguity of "half of 2, 2, 3" serves as a valuable lesson in the importance of clear and unambiguous communication in mathematics and other fields. It underscores the necessity of:
- Precise Notation: Using appropriate mathematical symbols to avoid ambiguity and ensure clarity.
- Contextual Understanding: Considering the context in which a problem is presented to interpret it correctly.
- Critical Thinking: Evaluating different interpretations and their underlying assumptions before arriving at a solution.
- Communicating Effectively: Clearly expressing mathematical problems and solutions to avoid misunderstandings.
This seemingly simple problem extends beyond basic arithmetic; it's a powerful illustration of the importance of careful phrasing, precise communication, and the multiple approaches available when tackling ambiguous problems. It highlights the need for critical thinking and the value of systematically exploring all potential interpretations before reaching a conclusion. Ultimately, the "correct" answer depends entirely on the intended interpretation, emphasizing the crucial role of clear communication in all aspects of mathematics and beyond. The exercise serves as a reminder that even simple-looking problems can hold surprising complexity and challenge our assumptions.
Latest Posts
Latest Posts
-
Hair Analysis Review And Reinforcement
Sep 09, 2025
-
Which Statement Best Describes Ethics
Sep 09, 2025
-
What Is 25km In Mph
Sep 09, 2025
-
Inputs Of Electron Transport Chain
Sep 09, 2025
-
5 Ft 10 In Centimetres
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.