Half Of 2 3 8
gasmanvison
Sep 06, 2025 · 5 min read
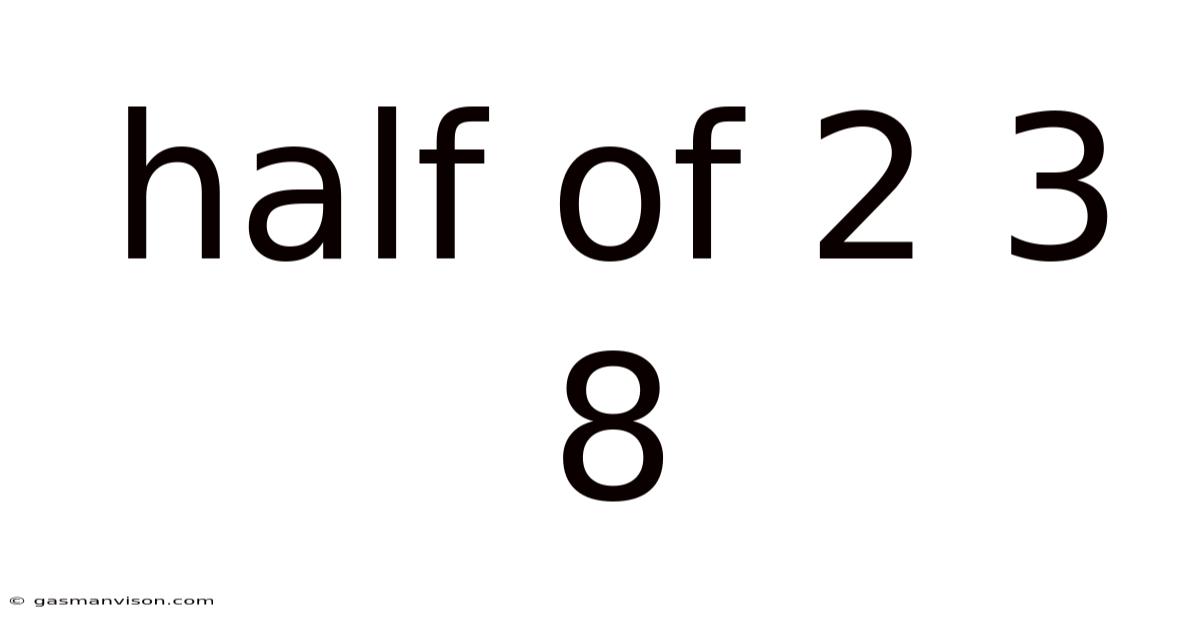
Table of Contents
Decoding "Half of 2, 3, 8": A Deep Dive into Fractions, Percentages, and Their Applications
This seemingly simple phrase, "half of 2, 3, 8," opens a door to a fascinating exploration of fundamental mathematical concepts. It's more than just a basic arithmetic problem; it's a springboard for understanding fractions, percentages, their real-world applications, and even delving into more advanced mathematical ideas. This article will dissect the meaning of "half of 2, 3, 8," explore different ways to calculate it, and highlight its relevance in various fields.
What Does "Half of 2, 3, 8" Mean?
The phrase itself implies finding half the value of each of the numbers 2, 3, and 8. In simpler terms, it's asking us to calculate one-half (1/2) of each number. This involves dividing each number by 2 or multiplying each number by 0.5 (which is the decimal equivalent of 1/2). This seemingly simple operation forms the basis for many complex calculations and real-world problems. Understanding this concept thoroughly unlocks a deeper comprehension of mathematical principles and their practical applications.
Calculating Half of 2, 3, and 8
Let's break down the calculation for each number:
- Half of 2: 2 / 2 = 1 or 2 * 0.5 = 1
- Half of 3: 3 / 2 = 1.5 or 3 * 0.5 = 1.5
- Half of 8: 8 / 2 = 4 or 8 * 0.5 = 4
Therefore, the answers are 1, 1.5, and 4 respectively. While seemingly straightforward, understanding the underlying principles of fractions and their relationship to division and multiplication is crucial for more complex scenarios.
Fractions: The Foundation of "Half"
The concept of "half" is fundamentally rooted in fractions. A fraction represents a part of a whole. In this case, "half" is represented by the fraction 1/2, where 1 is the numerator (the part we're interested in) and 2 is the denominator (the total number of parts). This fraction represents a ratio – one part out of two equal parts. Understanding fractions is essential not only for calculating halves but also for understanding proportions, ratios, and percentages. This understanding forms the basis for solving more complex problems involving ratios and proportions, even those that involve larger numbers and more complex fractions.
Percentages: Another Way to Express "Half"
"Half" can also be expressed as a percentage. Since a whole represents 100%, half of that whole is 50%. This means that finding half of a number is equivalent to finding 50% of that number. Converting fractions to percentages and vice-versa is a vital skill in various fields. For instance, in finance, understanding percentages is essential for calculating interest, discounts, and profit margins. This ability helps to understand data representation, particularly in financial reporting and investment analysis.
Real-World Applications of Finding "Half"
The seemingly simple act of finding "half" has wide-ranging applications across various disciplines:
-
Cooking and Baking: Recipe adjustments often require halving or doubling ingredients. Understanding fractions and percentages allows cooks to easily adapt recipes to the number of servings required. This is essential for efficient kitchen management and avoiding food waste. It also allows for consistent results across different quantities of servings.
-
Construction and Engineering: Dividing lengths, areas, and volumes in half is fundamental in various construction and engineering tasks. Precise measurements and calculations are crucial for ensuring structural integrity and safety. This is crucial for successful construction projects that adhere to safety standards and specifications.
-
Finance and Budgeting: Dividing budgets, calculating discounts, and determining profit margins all involve working with fractions and percentages. Financial literacy relies heavily on this skill. This is essential for personal financial management and business financial planning.
-
Data Analysis and Statistics: Representing data using fractions and percentages is crucial in data analysis and statistics. Understanding these concepts helps in interpreting data effectively and drawing meaningful conclusions. This enables better interpretation of data sets and informs decision-making processes.
-
Everyday Life: From sharing items equally to calculating discounts, the ability to find "half" simplifies everyday tasks and improves problem-solving abilities. This encompasses tasks from sharing snacks among children to calculating sale prices in shops.
Expanding the Concept: Beyond "Half"
The principle of finding a fraction of a number extends beyond "half." We can apply the same logic to find one-third (1/3), one-quarter (1/4), or any other fraction of a number. This involves understanding the concepts of division and multiplication within the context of fractions. Mastering these concepts provides a solid foundation for tackling more advanced mathematical topics, including algebra and calculus.
Advanced Applications: Ratios and Proportions
Understanding "half" also lays the groundwork for understanding ratios and proportions. A ratio is a comparison of two quantities, often expressed as a fraction. A proportion is a statement that two ratios are equal. Solving problems involving ratios and proportions is crucial in various fields, including:
-
Scaling Drawings and Models: Architects and engineers use ratios and proportions to scale down designs into smaller models or drawings, representing the object or space with accurate proportions.
-
Mixing Ingredients: In chemistry and cooking, precise ratios of ingredients are critical to obtain desired results. An understanding of ratios ensures consistency in the outcome.
-
Mapping and Geography: Maps use scales, which are ratios, to represent the size of a real-world location on a smaller map. Understanding these scales is crucial for interpreting maps correctly.
Connecting to Algebra and Beyond
The concept of "half" seamlessly integrates into algebraic concepts. For instance, finding "half of x" can be represented as (1/2)x or 0.5x. This simple representation opens doors to solving more complex algebraic equations involving fractions and variables. This understanding allows for more complex problem-solving using algebraic methods.
Conclusion: The Significance of a Simple Concept
While the phrase "half of 2, 3, 8" might seem trivial, its underlying mathematical concepts are far-reaching and incredibly important. Understanding fractions, percentages, ratios, and proportions is essential for navigating a wide variety of situations, both in academic settings and in everyday life. Mastering these fundamentals builds a strong foundation for more advanced mathematical studies and significantly improves problem-solving skills across various disciplines. The ability to confidently calculate "half" and its broader applications is a key component of mathematical literacy and contributes to overall cognitive development. From simple cooking tasks to complex engineering calculations, the ability to accurately and efficiently work with fractions and percentages proves invaluable. Therefore, the seemingly simple calculation holds far greater significance than it initially appears, forming a fundamental building block for countless mathematical applications.
Latest Posts
Latest Posts
-
Is 169 A Perfect Square
Sep 07, 2025
-
Happy Anniversary In French Language
Sep 07, 2025
-
How Far Is 200 Meters
Sep 07, 2025
-
Summary For The Secret Garden
Sep 07, 2025
-
Molecular Formula For Dinitrogen Monoxide
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.