How Many 1/3 Equals 3/4
gasmanvison
Sep 15, 2025 · 5 min read
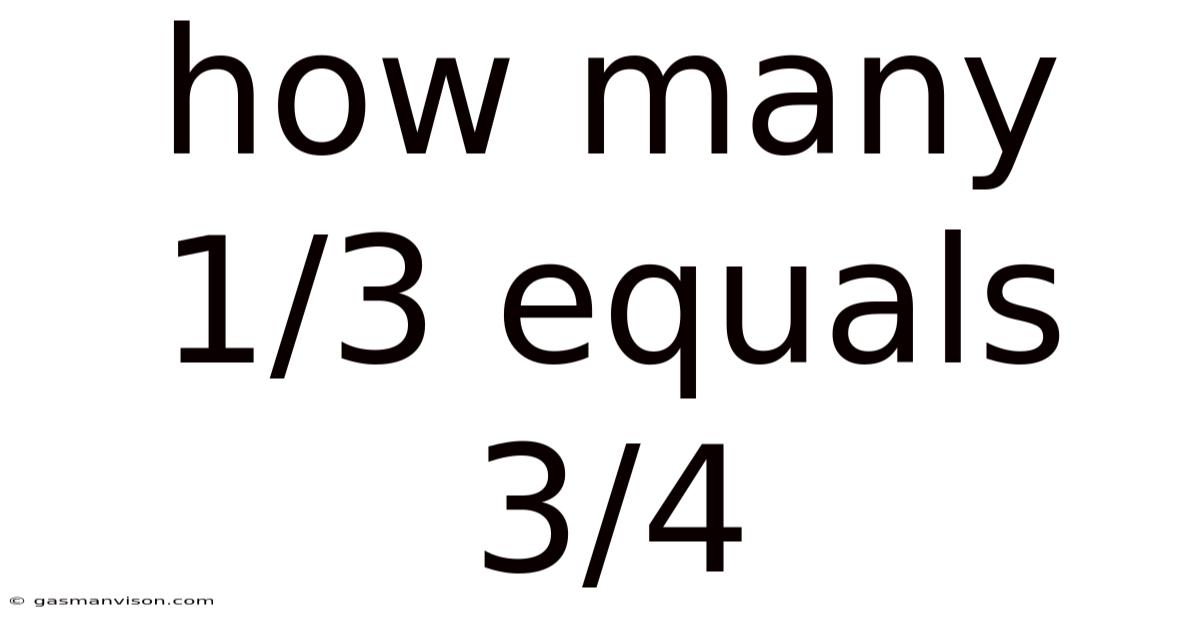
Table of Contents
How Many 1/3 Equals 3/4? Unpacking Fractions and Solving the Equation
This seemingly simple question, "How many 1/3 equals 3/4?", delves into the fundamental concepts of fractions, division, and algebraic manipulation. While the answer might seem immediately apparent to some, understanding the underlying process is crucial for mastering more complex mathematical problems. This article will not only provide the solution but also explore the various methods for solving this type of fractional equation, highlighting the importance of understanding fractional equivalence and applying appropriate mathematical techniques. We'll also touch upon practical applications and explore related concepts to provide a comprehensive understanding.
Understanding the Problem: A Foundation in Fractions
Before diving into the solution, let's clarify the question. We are essentially asking: "What number, when multiplied by 1/3, will give us 3/4?" This translates into an algebraic equation that we can solve. Understanding this translation is key to approaching similar problems. The core concepts involve:
- Fractions: Representing parts of a whole. Understanding numerators (top number) and denominators (bottom number) is vital.
- Equivalence: Recognizing that different fractions can represent the same value (e.g., 1/2 = 2/4 = 3/6).
- Algebra: Using variables (letters) to represent unknown quantities and manipulating equations to solve for them.
Method 1: Solving through Direct Algebraic Manipulation
Let's represent the unknown number as 'x'. The problem can be written as an algebraic equation:
(1/3) * x = 3/4
To solve for 'x', we need to isolate it on one side of the equation. We can do this by multiplying both sides by the reciprocal of 1/3, which is 3/1 (or simply 3):
(3/1) * (1/3) * x = (3/1) * (3/4)
This simplifies to:
x = (3 * 3) / (1 * 4)
x = 9/4
Therefore, nine-fourths (9/4) is the answer. This is also equivalent to 2 ¼ or 2.25.
Method 2: Using Cross-Multiplication
Another effective approach to solving fractional equations like this is cross-multiplication. This method is particularly useful when dealing with proportions. We can rewrite the equation as a proportion:
1/3 = 3/4x
Now, cross-multiply:
1 * 4x = 3 * 3
4x = 9
Divide both sides by 4 to isolate 'x':
x = 9/4
Again, we arrive at the same solution: x = 9/4 (or 2 ¼ or 2.25).
Method 3: Visualizing with Diagrams
While not a strictly algebraic method, visualizing the problem using diagrams can help build intuition and understanding, especially for those who are visually inclined.
Imagine a whole divided into thirds. We want to find how many of these thirds make up three-quarters of a whole. Dividing a whole into quarters, three-quarters would represent three out of four equal parts.
To visually compare, you would need to find a common denominator between 3 and 4, which is 12. This would allow you to visualize both fractions within the same whole, divided into twelve equal parts. Three-quarters would be represented by 9/12, and one-third would be represented by 4/12. By comparing the two, it becomes evident that nine-fourths (9/4) times one-third (4/12) results in three-quarters (9/12). This visual representation reinforces the algebraic solution.
Practical Applications and Real-World Examples
Understanding how to solve fractional equations has wide-ranging applications in various fields:
- Baking and Cooking: Scaling recipes up or down requires manipulating fractions. For example, if a recipe calls for 1/3 cup of sugar and you want to make 3/4 of the recipe, you'd need to calculate (1/3) * (3/4) cups of sugar.
- Construction and Engineering: Measuring and cutting materials often involves precise fractional calculations.
- Finance: Calculating percentages, interest rates, and proportions in financial planning.
- Data Analysis: Working with proportions and ratios in statistical analysis.
- Computer Programming: Many programming tasks involve fractional calculations, especially in graphics and game development.
Expanding Understanding: Related Concepts
This problem also provides an opportunity to explore several related mathematical concepts:
- Reciprocal: The reciprocal of a fraction is obtained by inverting the numerator and denominator. Understanding reciprocals is essential for solving fractional equations.
- Improper Fractions and Mixed Numbers: The solution (9/4) is an improper fraction (numerator is larger than the denominator). Converting it to a mixed number (2 ¼) offers a more intuitive representation in certain contexts.
- Decimal Equivalents: Fractions can be expressed as decimals (9/4 = 2.25). This conversion is often helpful for calculations or comparisons.
- Least Common Multiple (LCM) and Greatest Common Factor (GCF): Finding the LCM and GCF can simplify calculations involving fractions, particularly when adding, subtracting, or comparing them.
Conclusion: Mastering Fractions for a Broader Mathematical Understanding
The question, "How many 1/3 equals 3/4?", might appear simple at first glance, but it serves as an excellent starting point for understanding and mastering crucial concepts in mathematics. Through direct algebraic manipulation, cross-multiplication, and even visualization, we have demonstrated that the answer is 9/4 (or 2 ¼ or 2.25). However, the true value lies in grasping the underlying principles of fractional equivalence, algebraic techniques, and the diverse applications of these concepts in real-world scenarios. By strengthening your understanding of fractions, you build a solid foundation for more advanced mathematical problem-solving. Furthermore, mastering these techniques allows you to confidently tackle more complex equations and readily apply them to various fields requiring numerical precision and analysis. The journey from a simple fraction problem to a deeper understanding of mathematical principles highlights the power of consistent learning and the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
50 Grams Water To Tablespoons
Sep 15, 2025
-
Why Are Asian Eyes Slanted
Sep 15, 2025
-
Square Root Of 40 Simplified
Sep 15, 2025
-
A 2 Person Relay Race
Sep 15, 2025
-
Increased Explicit Defence Modifier Magnitudes
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/3 Equals 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.