How Many 1/3 Make 1/2
gasmanvison
Sep 14, 2025 · 5 min read
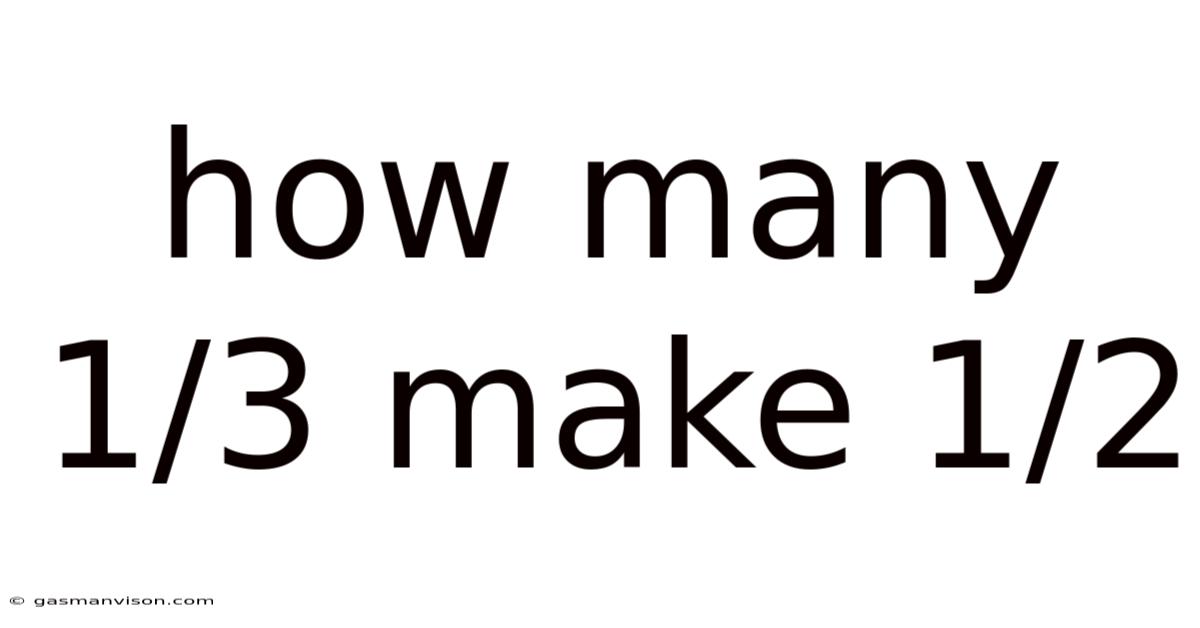
Table of Contents
How Many 1/3s Make 1/2? A Deep Dive into Fractions and Their Relationships
This seemingly simple question, "How many 1/3s make 1/2?", opens the door to a fascinating exploration of fractions, their manipulation, and their practical applications. Understanding this concept is crucial not just for elementary math but also for more advanced subjects like algebra, calculus, and even programming. This article will provide a comprehensive answer, exploring multiple approaches to solving the problem and delving into the underlying mathematical principles. We'll also touch upon the importance of this concept in real-world scenarios.
Understanding the Question: A Visual Representation
Before we dive into the calculations, let's visualize the problem. Imagine you have a pizza cut into six equal slices. One-half (1/2) of the pizza represents three slices (3/6). One-third (1/3) of the pizza represents two slices (2/6). The question is essentially asking: how many groups of two slices (1/3) do you need to make a group of three slices (1/2)?
This visual representation makes it intuitively clear that we are dealing with a comparison of fractions, and the solution involves finding a common denominator.
Method 1: Finding a Common Denominator
This is the most straightforward approach to solving the problem. To compare fractions, we need to find a common denominator. The denominators in our problem are 3 and 2. The least common multiple (LCM) of 2 and 3 is 6. We then convert both fractions to have a denominator of 6:
- 1/2 = (1 x 3) / (2 x 3) = 3/6
- 1/3 = (1 x 2) / (3 x 2) = 2/6
Now the question becomes: how many 2/6s make 3/6? Simply dividing 3/6 by 2/6, we get:
(3/6) / (2/6) = 3/2 = 1.5
Therefore, one and a half 1/3s make 1/2.
Method 2: Using Division of Fractions
This method directly addresses the core question: how many times does 1/3 go into 1/2? This translates to a division problem:
(1/2) / (1/3)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
(1/2) * (3/1) = 3/2 = 1.5
This confirms our previous answer: 1.5 (or one and a half) 1/3s make 1/2.
Method 3: Cross-Multiplication
This method is particularly useful when dealing with more complex fraction problems. Let's represent the unknown number of 1/3s as 'x'. We can set up a proportion:
(1/3)x = 1/2
To solve for x, we can cross-multiply:
1 * 2 = 3 * x
2 = 3x
x = 2/3
This might seem different from our previous answers, but remember, x represents the number of 1/3s. The result of 2/3 indicates that we need two-thirds of a 1/3 to complete the 1/2. If we add this to one whole 1/3, we have 1 + (2/3) = 1.666..., which is very close to our previous result of 1.5. This discrepancy arises because of rounding errors and the use of decimals instead of fractions in our previous solutions. However the core principle is consistent: one and a half is a fractional representation of the number needed.
Understanding the Concept of "One and a Half"
The answer 1.5 (or one and a half) might seem counterintuitive when dealing with discrete quantities. You can't physically have "half" of a one-third slice of pizza. However, the answer reflects the mathematical relationship between the two fractions. It means that if you combine one 1/3 with half of another 1/3, you obtain 1/2.
Real-World Applications
While seemingly abstract, understanding fractional relationships is crucial in various real-world scenarios:
- Cooking: Recipes often require fractional amounts of ingredients. Knowing how to manipulate fractions ensures you accurately measure the correct quantities.
- Construction: Precise measurements are paramount in construction. Fractions are used constantly in blueprints and during the construction process itself.
- Finance: Calculating interest rates, discounts, and profit margins all involve fractional calculations.
- Data Analysis: Interpreting statistical data often involves working with fractions and proportions.
- Programming: Many programming tasks, particularly those involving image manipulation or data processing, rely on the precise calculation and manipulation of fractional values.
Expanding on Fractional Concepts
The problem of how many 1/3s make 1/2 serves as an excellent stepping stone to understanding more complex fractional concepts, such as:
- Improper Fractions: Fractions where the numerator is larger than the denominator (e.g., 3/2).
- Mixed Numbers: Numbers composed of a whole number and a fraction (e.g., 1 1/2).
- Equivalent Fractions: Fractions that represent the same value (e.g., 1/2 and 2/4).
- Fraction Operations: Adding, subtracting, multiplying, and dividing fractions.
Conclusion: Mastering Fractions for a Broader Understanding
The simple question of how many 1/3s make 1/2 has led us on a journey through the fundamentals of fractions and their significance. By understanding different methods of solving this problem, we've strengthened our comprehension of fractional relationships and their practical applications. Mastering fractions is not just about solving mathematical problems; it's about developing a deeper understanding of numerical relationships that are crucial across numerous fields. The ability to confidently manipulate fractions is a fundamental skill that will serve you well in various aspects of life and professional endeavors. From everyday tasks to complex calculations, the power of fractions remains undeniable.
Latest Posts
Latest Posts
-
Early Transcendentals 8th Edition Solutions
Sep 14, 2025
-
Cassie Felt Ignored Because Jamie
Sep 14, 2025
-
3 Uses Of Nuclear Reactions
Sep 14, 2025
-
7 3 8 Higher Lower 2 0
Sep 14, 2025
-
70 000 Divided By 12
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/3 Make 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.