How Many 1/4 In 3/4
gasmanvison
Sep 10, 2025 · 5 min read
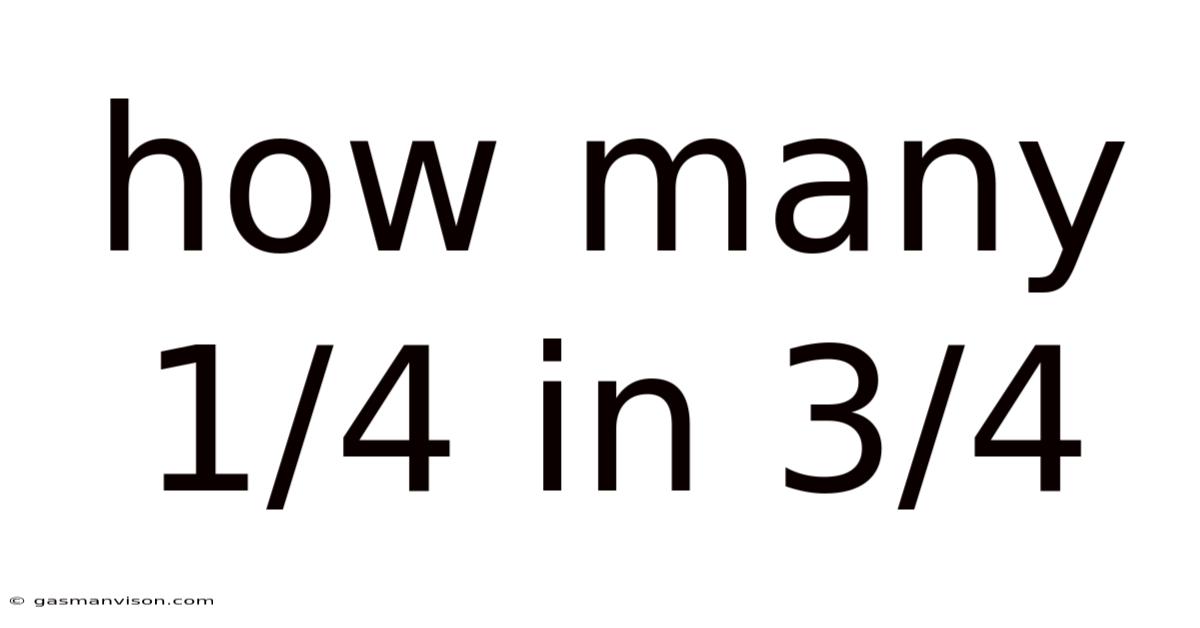
Table of Contents
How Many 1/4s Are in 3/4? A Deep Dive into Fractions
This seemingly simple question, "How many 1/4s are in 3/4?", opens the door to a deeper understanding of fractions, division, and even real-world applications. While the answer might seem immediately obvious to some, exploring the various methods for solving this problem, and understanding the underlying mathematical principles, is crucial for building a strong foundation in mathematics. This article will not only answer the question but also provide a comprehensive explanation, exploring different approaches and relating the concept to practical examples. This will equip you with the knowledge and skills to confidently tackle similar fractional problems in the future.
Understanding Fractions: A Quick Refresher
Before diving into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we have.
In our problem, we have two fractions: 1/4 and 3/4. 1/4 represents one part out of four equal parts, while 3/4 represents three parts out of four equal parts. Understanding this foundational concept is key to solving the problem effectively.
Method 1: Visual Representation
One of the easiest ways to understand how many 1/4s are in 3/4 is through a visual representation. Imagine a pizza cut into four equal slices. Each slice represents 1/4 of the pizza. If you have 3 slices, you have 3/4 of the pizza. By simply counting the slices, you can see that there are three 1/4 slices in 3/4 of the pizza.
This visual method is particularly helpful for beginners, as it provides a concrete representation of the abstract concept of fractions. It allows for a clear and intuitive understanding of the relationship between the two fractions.
Method 2: Division of Fractions
A more formal mathematical approach involves dividing fractions. To find out how many 1/4s are in 3/4, we can set up a division problem: (3/4) ÷ (1/4).
Remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/4 is 4/1 (or simply 4). Therefore, our problem becomes:
(3/4) × (4/1) = (3 × 4) / (4 × 1) = 12 / 4 = 3
This calculation clearly shows that there are three 1/4s in 3/4. This method provides a more rigorous and generalizable solution, applicable to a wider range of fractional division problems.
Method 3: Understanding Equivalent Fractions
Another way to approach this problem is by understanding equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. We can express 3/4 as an equivalent fraction with a denominator of 1. To do this, we need to find a number that, when multiplied by the denominator (4), gives us 1. There isn't a whole number that will do this, but we can work with the concept of dividing 3/4 into parts of 1/4. We can express 3/4 as three of 1/4.
This method reinforces the understanding that 3/4 is simply three equal parts of a total of four equal parts. It directly shows that there are three 1/4s in 3/4.
Real-World Applications
Understanding how to work with fractions like 1/4 and 3/4 has numerous real-world applications:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Knowing how to convert and work with fractions is essential for accurate measurements and successful cooking. For example, if a recipe calls for 3/4 cup of flour and you only have a 1/4 cup measuring cup, you'll need to use it three times.
-
Construction and Engineering: Precision is crucial in construction and engineering. Workers often deal with fractional measurements when cutting materials or calculating distances. Understanding fractions ensures accuracy and prevents errors. Imagine cutting a pipe that requires a length of 3/4 of a meter, and you only have a 1/4 meter measuring tool. You would need to use it three times.
-
Finance and Budgeting: Fractions are commonly used in financial calculations, such as calculating percentages, interest rates, or proportions of a budget. For example, if you need to save 3/4 of your income and receive a 1/4 income each month, you would need to save your income from three months.
-
Time Management: We often represent time using fractions. For example, 1/4 of an hour is 15 minutes, and 3/4 of an hour is 45 minutes. Understanding this relationship is crucial for effective time management and scheduling.
-
Data Analysis: In data analysis, fractions are often used to represent proportions or percentages of a dataset. For example, if 3/4 of respondents answered "yes" to a survey question, that means 75% responded positively.
Expanding the Concept: Working with Different Fractions
The principles discussed above can be applied to a wide range of fraction problems. Let's consider a slightly more complex example: how many 1/8s are in 3/4?
First, we need to find a common denominator. The least common multiple of 4 and 8 is 8. We can convert 3/4 to an equivalent fraction with a denominator of 8:
3/4 = (3 × 2) / (4 × 2) = 6/8
Now, we can divide 6/8 by 1/8:
(6/8) ÷ (1/8) = (6/8) × (8/1) = 48/8 = 6
Therefore, there are six 1/8s in 3/4.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
The seemingly simple question, "How many 1/4s are in 3/4?", has served as a gateway to explore the intricacies of fractions, different problem-solving approaches, and their wide-ranging practical applications. By understanding the various methods—visual representation, division of fractions, and working with equivalent fractions—you've built a stronger foundation for tackling more complex fractional problems. The ability to confidently work with fractions is an invaluable skill applicable across numerous disciplines, from everyday life to specialized fields. Remember, the key is to approach these problems systematically, selecting the method that best suits your understanding and the complexity of the problem at hand. Through practice and a clear understanding of the underlying principles, mastering fractions becomes achievable, paving the way for success in more advanced mathematical concepts.
Latest Posts
Latest Posts
-
In General Critical Thinking Means
Sep 11, 2025
-
What Does Thug Life Mean
Sep 11, 2025
-
Rural Areas Have Of Development
Sep 11, 2025
-
The Abbreviation For Biopsy Is
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 In 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.