If Xyz Rst Find Rs
gasmanvison
Sep 18, 2025 · 5 min read
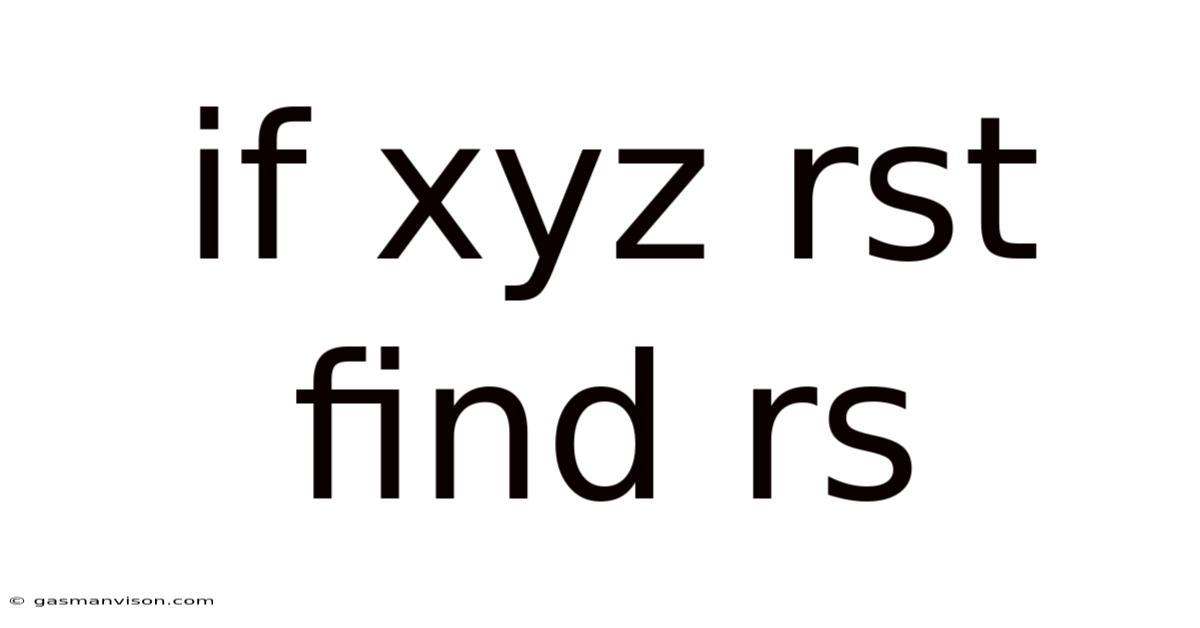
Table of Contents
If XYZ = RST, Find RS: A Comprehensive Guide to Solving Algebraic Equations
This article delves into the intricacies of solving algebraic equations, specifically focusing on problems presented in the format "If XYZ = RST, find RS." We'll explore various approaches, from fundamental algebraic manipulations to more advanced techniques, ensuring a comprehensive understanding for readers of all levels. This guide will equip you with the skills to confidently tackle similar problems and build a strong foundation in algebra.
Meta Description: Learn how to solve algebraic equations of the form "If XYZ = RST, find RS". This comprehensive guide covers various methods, from basic algebraic manipulation to advanced techniques, ensuring a thorough understanding for all levels. Master equation solving and enhance your algebraic skills.
Understanding the Problem: Deconstructing "If XYZ = RST, Find RS"
The statement "If XYZ = RST, find RS" presents an algebraic equation where XYZ and RST represent numbers or algebraic expressions. The core challenge lies in determining the value or expression for RS given the equality of XYZ and RST. The problem highlights the importance of understanding the relationship between the variables and skillfully manipulating the equation to isolate the desired term, RS. This seemingly simple problem can involve various complexities depending on the nature of X, Y, Z, R, S, and T.
We need to clarify a crucial point: The problem as stated, "If XYZ = RST, find RS," is ambiguous. XYZ and RST are not standard mathematical notations. They could represent:
- Concatenation: XYZ might mean the number formed by concatenating the digits X, Y, and Z (e.g., if X=1, Y=2, Z=3, then XYZ = 123). Similarly for RST. In this case, the problem becomes a number puzzle.
- Multiplication: XYZ might represent X * Y * Z. Similarly, RST might represent R * S * T. This interpretation leads to a typical algebraic equation.
- Variables in an equation: X, Y, Z, R, S, and T could represent variables within a larger algebraic expression.
To solve the problem effectively, we must first clarify the intended meaning of XYZ and RST. We will explore solutions based on the most common interpretation – multiplication. However, the principles and techniques discussed can be adapted to other interpretations.
Solving "If X * Y * Z = R * S * T, Find RS" using Algebraic Manipulation
Assuming XYZ and RST represent the products XYZ and RST respectively, our goal is to find RS, given that X * Y * Z = R * S * T. Directly solving for RS without additional information is impossible. We lack sufficient equations to determine the individual values of R and S.
Scenario 1: Additional Information Provided
If additional information is provided, such as the values of some variables or relationships between them, we can solve for RS. Let's consider some examples:
Example 1: If X=2, Y=3, Z=4, R=1, T=24, find RS.
- Substitute the known values: 2 * 3 * 4 = 1 * S * 24
- Simplify: 24 = 24S
- Solve for S: S = 24 / 24 = 1
- We still need R: Without knowing R, we cannot find RS. The problem is underspecified.
Example 2: If X=2, Y=3, Z=4, R=1, and S=6, find RS.
- Substitute known values: 2 * 3 * 4 = 1 * 6 * T
- Simplify: 24 = 6T
- Solve for T: T = 24 / 6 = 4
- Calculate RS: RS = 1 * 6 = 6
In this case, we were able to find RS because sufficient information was given.
Scenario 2: Exploring Relationships and Simplifications
Even without specific numerical values, we can explore potential relationships and simplifications. For instance, if we knew that X = R, Y = T, and Z = S, then the equation X * Y * Z = R * S * T would immediately simplify to X * Y * Z = X * Z * Y (which is always true due to the commutative property of multiplication). This would not help us find RS directly, but it illustrates how understanding relationships between variables can be crucial.
Advanced Techniques and Considerations
For more complex scenarios, advanced algebraic techniques might be necessary. These include:
- Factorization: If the expressions XYZ and RST can be factored, this can simplify the equation and potentially lead to a solution for RS.
- Substitution: Introducing substitution variables can help simplify the equation and make it easier to solve.
- Systems of Equations: If multiple equations involving X, Y, Z, R, S, and T are provided, we can use techniques for solving systems of equations to find RS.
Addressing the Ambiguity: Other Interpretations of XYZ and RST
Let's briefly touch upon other possible interpretations of XYZ and RST:
-
Concatenation: If XYZ and RST represent concatenated numbers, the problem transforms into a number puzzle. Solving this would require techniques specific to number manipulation and potentially trial and error.
-
Variables in a Larger Equation: If XYZ and RST are parts of a more complex equation, then we would need the entire equation to solve for RS. The solution would depend entirely on the context of the larger expression.
Conclusion: The Importance of Context and Clear Problem Definition
The problem "If XYZ = RST, find RS" highlights the crucial role of clear problem definition and the importance of understanding context in mathematics and problem-solving. Without additional information or clarification on the meaning of XYZ and RST, a definitive solution for RS cannot be obtained. This problem serves as a valuable lesson in the careful interpretation of mathematical statements and the need for sufficient information to reach a valid solution. Mastering basic algebraic manipulation and adapting techniques based on the context of the problem are key skills for success in algebra and beyond. The ability to analyze the given information, identify missing pieces, and strategize the solution path are crucial aspects of problem-solving that extend far beyond the realm of algebraic equations. Remember to always check your work and consider alternative approaches to ensure accuracy and completeness.
Latest Posts
Latest Posts
-
Was Obama The Youngest President
Sep 18, 2025
-
5 To The Third Power
Sep 18, 2025
-
4 X 2 X 7
Sep 18, 2025
-
Ca Oh 2 Compound Name
Sep 18, 2025
-
Is Granite Homogeneous Or Heterogeneous
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about If Xyz Rst Find Rs . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.