Is 1/4 Equivalent To 1/8
gasmanvison
Sep 23, 2025 · 6 min read
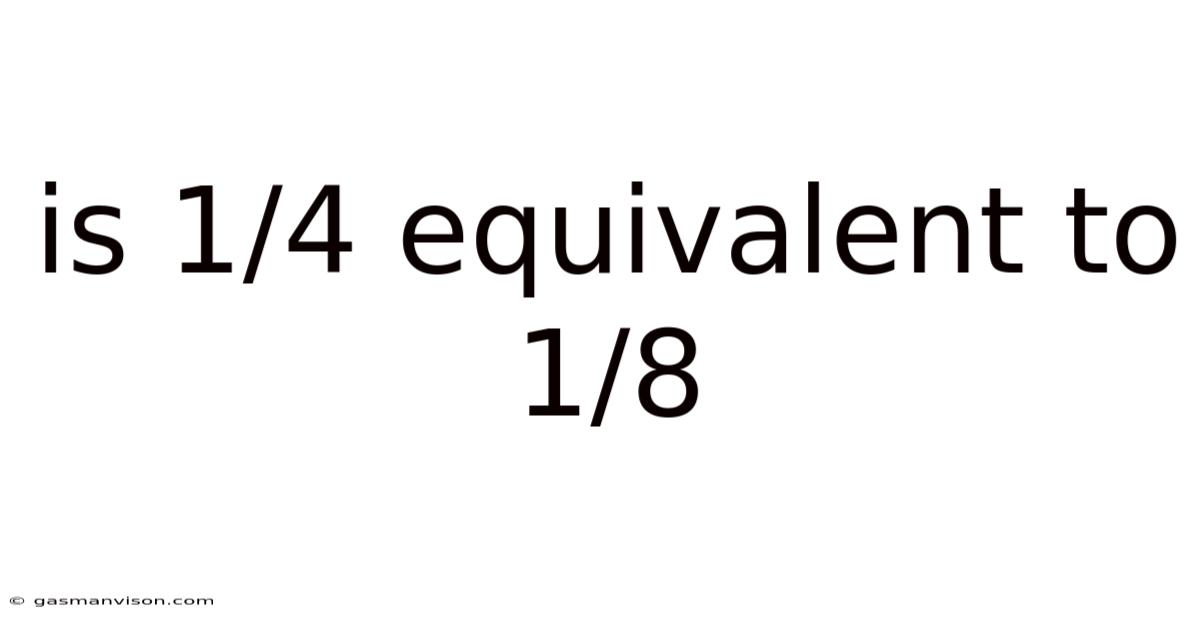
Table of Contents
Is 1/4 Equivalent to 1/8? A Deep Dive into Fraction Equivalence
Meta Description: This article explores the fundamental concept of fraction equivalence, focusing on whether 1/4 is equal to 1/8. We'll delve into visual representations, mathematical proofs, and real-world examples to clarify this common misconception. Learn how to identify equivalent fractions and master the basics of fractions.
The question, "Is 1/4 equivalent to 1/8?" is a deceptively simple one that often trips up students and even adults grappling with fractions. The quick answer is no, they are not equivalent. However, understanding why they aren't equivalent and grasping the broader concept of fraction equivalence is crucial for a solid foundation in mathematics. This article will not only answer the question definitively but also equip you with the tools to confidently tackle similar comparisons and manipulations of fractions.
Understanding Fractions: Parts of a Whole
Before diving into the equivalence question, let's establish a firm understanding of what a fraction represents. A fraction, like 1/4 or 1/8, expresses a part of a whole. The number on the top, called the numerator, indicates how many parts you have. The number on the bottom, called the denominator, shows how many equal parts the whole is divided into.
So, 1/4 means you have one part out of a whole that's been divided into four equal parts. Similarly, 1/8 represents one part out of a whole divided into eight equal parts.
Visualizing the Difference: The Power of Diagrams
One of the most effective ways to understand why 1/4 and 1/8 are not equivalent is through visual representation. Imagine a pizza.
-
1/4: If you cut the pizza into four equal slices, 1/4 represents one of those slices. It's a relatively large portion.
-
1/8: If you cut the same pizza into eight equal slices, 1/8 represents only one of those smaller slices.
Clearly, one large slice (1/4) is much bigger than one small slice (1/8). This visual demonstration immediately clarifies that they are not equal. You can apply this same principle to other objects divided into equal parts – a chocolate bar, a pie, or even a geometric shape.
Mathematical Proof: Equivalent Fractions and Simplification
While visual aids are helpful, a mathematical proof provides a more rigorous demonstration. Equivalent fractions are fractions that represent the same value, even though they look different. You can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example, 2/4 is equivalent to 1/2 because you can simplify 2/4 by dividing both the numerator and the denominator by 2 (2 ÷ 2 = 1 and 4 ÷ 2 = 2).
To determine if 1/4 and 1/8 are equivalent, we look for a common multiplier or divisor that would transform one into the other. There isn't one. You cannot multiply or divide both the numerator and denominator of 1/4 by any number to get 1/8, and vice versa. Therefore, they are not equivalent.
Common Mistakes and Misconceptions
A common mistake is to focus solely on the numerators. Some might incorrectly assume that because both fractions have a "1" on top, they must be equal. However, the denominator plays a crucial role in defining the size of each fraction. A larger denominator means the whole is divided into more parts, resulting in smaller individual parts.
Expanding the Concept: Finding Equivalent Fractions
Let's explore how to find equivalent fractions. Consider the fraction 1/2. To find an equivalent fraction, we can multiply both the numerator and the denominator by the same number:
- Multiply by 2: (1 x 2) / (2 x 2) = 2/4
- Multiply by 3: (1 x 3) / (2 x 3) = 3/6
- Multiply by 4: (1 x 4) / (2 x 4) = 4/8
All these fractions (1/2, 2/4, 3/6, 4/8) are equivalent because they represent the same portion of a whole. The process of finding equivalent fractions is reversible; you can simplify a fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Real-World Applications of Fraction Equivalence
Understanding fraction equivalence is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often require adjustments. If a recipe calls for 1/2 cup of sugar, and you only have 1/4 cup measuring cups, you'll need to use two 1/4 cups to get the equivalent amount.
-
Measurement and Construction: Precision in measurements is vital, and understanding equivalent fractions allows for flexibility in using different measuring tools.
-
Finance: Understanding fractions is crucial for managing budgets, calculating percentages, and interpreting financial data.
-
Data Analysis: Representing data using fractions and understanding their equivalence is essential for accurate interpretation and comparison.
Beyond 1/4 and 1/8: Comparing Other Fractions
The principles we’ve discussed extend to comparing any two fractions. Here’s a step-by-step approach:
-
Find a Common Denominator: The easiest way to compare fractions is to find a common denominator – a number that is a multiple of both denominators.
-
Convert to Equivalent Fractions: Rewrite both fractions with the common denominator.
-
Compare Numerators: Once the denominators are the same, the fraction with the larger numerator represents the larger value.
For example, to compare 2/3 and 3/4, find a common denominator (12). Convert the fractions: 2/3 becomes 8/12, and 3/4 becomes 9/12. Since 9 > 8, 3/4 is greater than 2/3.
Mastering Fractions: Practice and Resources
Mastering fractions takes practice. There are numerous online resources, workbooks, and educational apps available to help you hone your skills. Consistent practice with various types of fraction problems will build your confidence and understanding. Don't be afraid to revisit the basics and use visual aids to reinforce your learning.
Conclusion: A Firm Grasp on Fraction Equivalence
The answer to "Is 1/4 equivalent to 1/8?" is a resounding no. This article has not only addressed this specific question but also provided a comprehensive exploration of fraction equivalence. Through visual representations, mathematical proofs, and real-world examples, we've illustrated the importance of understanding the relationship between the numerator and the denominator and how to identify and manipulate equivalent fractions. By mastering these fundamental concepts, you'll be well-equipped to tackle more complex mathematical challenges and confidently apply fraction knowledge in various aspects of life. Remember that practice and a willingness to explore different approaches are key to solidifying your understanding of fractions.
Latest Posts
Latest Posts
-
Unit Weight Of Water Units
Sep 23, 2025
-
How Tall Is 53 Inches
Sep 23, 2025
-
6 7 8 9 10
Sep 23, 2025
-
10 7w 13 7w 15
Sep 23, 2025
-
Lewis Dot Structure For Alcl3
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Equivalent To 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.