Is 1/8 Smaller Than 1/4
gasmanvison
Sep 13, 2025 · 5 min read
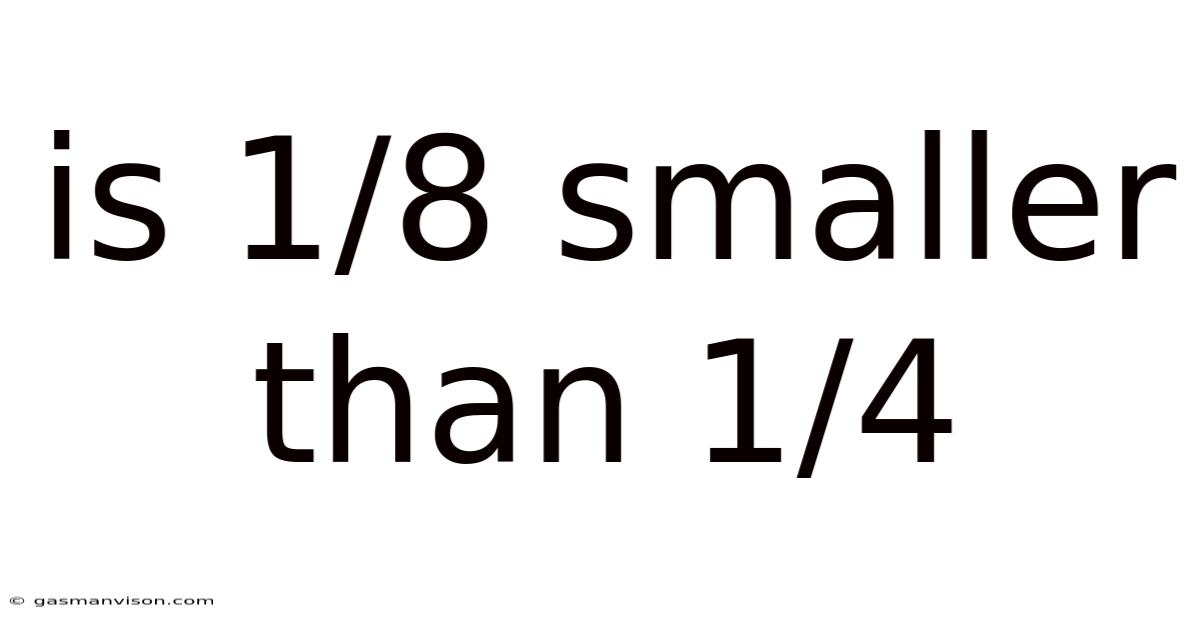
Table of Contents
Is 1/8 Smaller Than 1/4? A Deep Dive into Fractions and Their Comparisons
This seemingly simple question, "Is 1/8 smaller than 1/4?", opens the door to a broader understanding of fractions, their representation, and various methods for comparing them. While the answer is a straightforward "yes," the journey to understanding why is crucial for building a solid foundation in mathematics, particularly for anyone struggling with fractions or preparing for standardized tests like the SAT or ACT. This article will explore the concept in detail, providing multiple approaches to comparing fractions and reinforcing the understanding through various examples.
Meta Description: This comprehensive guide explains why 1/8 is smaller than 1/4, exploring different methods for comparing fractions, including visual representations, equivalent fractions, and decimal conversions. Perfect for students learning fractions or anyone looking to refresh their math skills.
Understanding Fractions: The Building Blocks
Before diving into the comparison, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the fractions 1/8 and 1/4, the numerators are both 1, meaning we are considering one part in each case. However, the denominators differ significantly: 8 and 4. This difference is key to understanding their relative sizes.
Visualizing the Comparison: The Pizza Analogy
One of the most effective ways to understand fractions is through visual representation. Imagine two pizzas of the same size:
- Pizza 1: Cut into 4 equal slices (representing 1/4).
- Pizza 2: Cut into 8 equal slices (representing 1/8).
If you take one slice from Pizza 1 (1/4), you have a larger piece than if you take one slice from Pizza 2 (1/8). This visual analogy clearly demonstrates that 1/8 is smaller than 1/4. The larger the denominator, the smaller each individual part becomes.
Using Equivalent Fractions for Comparison
Another powerful method for comparing fractions is to find equivalent fractions with a common denominator. This involves finding a common multiple of the denominators (8 and 4 in our case). The least common multiple (LCM) of 8 and 4 is 8.
- 1/4: To convert 1/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2: (1 x 2) / (4 x 2) = 2/8.
Now we can easily compare 1/8 and 2/8. Since 1 < 2, we can conclude that 1/8 < 2/8, which means 1/8 < 1/4.
Decimal Conversion: A Numerical Approach
Converting fractions to decimals provides another way to compare them. This method relies on dividing the numerator by the denominator:
- 1/4: 1 ÷ 4 = 0.25
- 1/8: 1 ÷ 8 = 0.125
By comparing the decimal values, 0.25 and 0.125, it's evident that 0.125 (1/8) is smaller than 0.25 (1/4). This approach is particularly helpful when dealing with more complex fractions.
Expanding the Concept: Comparing Fractions with Different Numerators
While our initial question focused on fractions with the same numerator (1), the principles discussed can be applied to fractions with different numerators. Let's consider comparing 3/8 and 2/4.
Again, finding equivalent fractions with a common denominator is a useful strategy. The LCM of 8 and 4 is 8:
- 2/4: Multiply both numerator and denominator by 2: (2 x 2) / (4 x 2) = 4/8
Now we compare 3/8 and 4/8. Since 3 < 4, we conclude that 3/8 < 4/8, meaning 3/8 < 2/4.
Number Line Representation: A Visual Aid for Ordering
A number line is a valuable tool for visualizing the relative sizes of fractions. By plotting both fractions on a number line scaled from 0 to 1, we can easily see which fraction lies closer to 0 (and therefore is smaller). For 1/8 and 1/4, 1/8 would be much closer to 0, reinforcing its smaller size.
Real-World Applications: Understanding Fractions in Everyday Life
Understanding fraction comparison isn't just an academic exercise. It has numerous real-world applications:
- Cooking and Baking: Following recipes often requires understanding fraction equivalents and comparisons (e.g., 1/2 cup is larger than 1/4 cup).
- Measurement and Construction: Precise measurements in various fields depend on accurate fraction understanding.
- Financial Calculations: Understanding percentages and proportions, which are based on fractions, is crucial for managing personal finances and investments.
- Data Analysis and Statistics: Representing data and interpreting results often involves working with fractions and percentages.
Troubleshooting Common Mistakes and Misconceptions
Many students struggle with fractions, often making these common mistakes:
- Confusing Numerator and Denominator: Understanding the roles of each part is fundamental.
- Incorrectly Finding Equivalent Fractions: Remember to multiply both the numerator and the denominator by the same number.
- Failing to Find a Common Denominator: This prevents direct comparison of fractions.
Advanced Techniques for Comparing Fractions: Cross-Multiplication
For more complex fractions, cross-multiplication offers a direct comparison method. To compare a/b and c/d, we cross-multiply:
- If a x d > b x c, then a/b > c/d
- If a x d < b x c, then a/b < c/d
- If a x d = b x c, then a/b = c/d
Let's apply this to 3/5 and 4/7:
- 3 x 7 = 21
- 5 x 4 = 20
Since 21 > 20, we conclude that 3/5 > 4/7.
Conclusion: Mastering Fractions for Mathematical Proficiency
The seemingly simple question, "Is 1/8 smaller than 1/4?", serves as a springboard for exploring the rich world of fractions. By understanding the various methods for comparing fractions – visualization, equivalent fractions, decimal conversion, number lines, and cross-multiplication – students can build a strong foundation in mathematics and apply this knowledge to numerous real-world scenarios. Consistent practice and a focus on understanding the underlying principles are key to mastering fractions and achieving mathematical proficiency. Remember, the more you practice, the more intuitive and effortless fraction comparison will become.
Latest Posts
Latest Posts
-
600 Ml How Many Ounces
Sep 13, 2025
-
53 Kg How Many Pounds
Sep 13, 2025
-
Convert 300 Ml To Oz
Sep 13, 2025
-
Frankenstein Quotes And Page Numbers
Sep 13, 2025
-
Blue Accent 5 Lighter 40
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/8 Smaller Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.