Is 2/3 Bigger Than 1/4
gasmanvison
Sep 20, 2025 · 5 min read
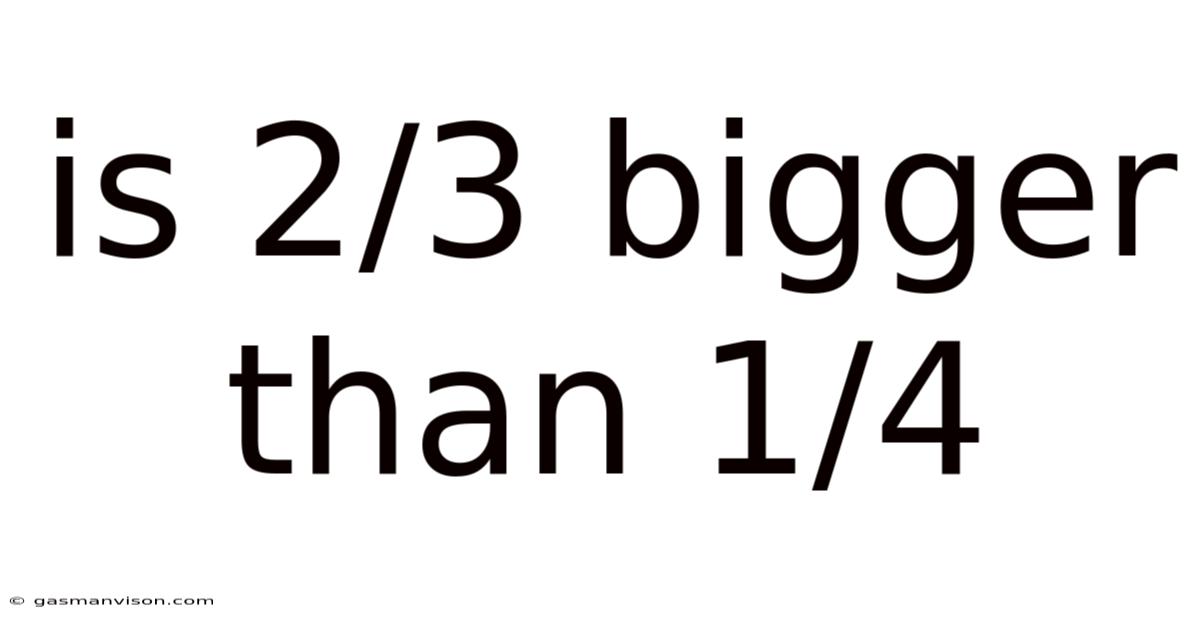
Table of Contents
Is 2/3 Bigger Than 1/4? A Deep Dive into Fraction Comparison
This article explores the question, "Is 2/3 bigger than 1/4?", going beyond a simple yes or no answer. We'll delve into various methods for comparing fractions, providing a comprehensive understanding of the concept for students and anyone looking to refresh their fraction skills. This will involve exploring different approaches, including visual representations, equivalent fractions, decimal conversions, and cross-multiplication. Understanding fraction comparison is fundamental in mathematics and has practical applications in numerous fields.
Meta Description: Learn how to compare fractions effectively! This in-depth guide explores multiple methods to determine if 2/3 is bigger than 1/4, including visual aids, equivalent fractions, decimal conversion, and cross-multiplication. Master fraction comparison today!
Visualizing Fractions: A Picture is Worth a Thousand Words
One of the easiest ways to compare fractions is through visualization. Imagine a single pizza. Dividing the pizza into three equal slices represents the denominator of 2/3. Two of these slices represent the numerator, 2/3 of the pizza.
Now, imagine another pizza, this time divided into four equal slices. 1/4 represents one of these slices. Visually comparing the two portions – two-thirds of one pizza versus one-quarter of another – it's immediately apparent that 2/3 is significantly larger than 1/4. This visual method works well for simpler fractions, providing an intuitive understanding of their relative sizes.
Finding Equivalent Fractions: Building a Common Ground
Another effective method involves finding equivalent fractions. Equivalent fractions represent the same portion but have different numerators and denominators. The key is to find a common denominator for both fractions. The common denominator is a number that both 3 and 4 divide into evenly. In this case, the least common multiple (LCM) of 3 and 4 is 12.
Let's convert both fractions to have a denominator of 12:
- 2/3: To change the denominator from 3 to 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
- 1/4: To change the denominator from 4 to 12, we multiply both the numerator and denominator by 3: (1 x 3) / (4 x 3) = 3/12
Now the comparison is straightforward: 8/12 is clearly larger than 3/12. Therefore, 2/3 (which is equal to 8/12) is bigger than 1/4 (which is equal to 3/12). This method is particularly useful when dealing with more complex fractions where visual comparison becomes less intuitive.
Decimal Conversions: Bridging the Gap Between Fractions and Decimals
Converting fractions to decimals provides another way to compare them. To convert a fraction to a decimal, divide the numerator by the denominator:
- 2/3: 2 ÷ 3 = 0.666... (a repeating decimal)
- 1/4: 1 ÷ 4 = 0.25
Comparing the decimal values, 0.666... is considerably larger than 0.25. This confirms that 2/3 is bigger than 1/4. This method is particularly helpful when using calculators or when dealing with fractions that are difficult to visualize or convert to equivalent fractions with a common denominator. Remember that rounding decimals might lead to slight inaccuracies, especially with repeating decimals; however, for practical purposes, this method provides a clear and efficient comparison.
Cross-Multiplication: A Direct Comparison Method
Cross-multiplication offers a direct and efficient method for comparing fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and vice versa. The larger product indicates the larger fraction.
Let's compare 2/3 and 1/4 using cross-multiplication:
- Multiply the numerator of 2/3 (which is 2) by the denominator of 1/4 (which is 4): 2 x 4 = 8
- Multiply the numerator of 1/4 (which is 1) by the denominator of 2/3 (which is 3): 1 x 3 = 3
Since 8 > 3, the fraction 2/3 is larger than 1/4. This method provides a quick and accurate comparison, particularly useful for more complex fractions where finding a common denominator might be time-consuming.
Comparing Fractions with Different Numerators and Denominators: A General Approach
The methods described above apply to various fraction comparisons, not just 2/3 and 1/4. Let's summarize the general approach for comparing any two fractions, a/b and c/d:
- Visual Representation: If the fractions are relatively simple, drawing diagrams can offer a quick visual comparison.
- Equivalent Fractions: Find the least common multiple (LCM) of the denominators (b and d). Convert both fractions to equivalent fractions with the LCM as the common denominator. Compare the numerators of the equivalent fractions.
- Decimal Conversion: Convert both fractions to decimals by dividing the numerator by the denominator. Compare the decimal values.
- Cross-Multiplication: Multiply the numerator of the first fraction (a) by the denominator of the second fraction (d) and the numerator of the second fraction (c) by the denominator of the first fraction (b). The larger product corresponds to the larger fraction. Remember to consider the direction of the inequality. If ad > bc, then a/b > c/d.
Beyond the Basics: Applications and Further Exploration
Understanding fraction comparison is crucial in numerous areas:
- Everyday Life: Comparing quantities, proportions, and measurements (e.g., comparing the amount of ingredients in a recipe).
- Cooking and Baking: Adjusting recipes based on the desired yield.
- Construction and Engineering: Calculating material requirements and dimensions.
- Finance: Understanding percentages, interest rates, and proportions of investments.
- Data Analysis: Interpreting data presented as fractions or proportions.
For further exploration, consider delving into:
- Improper Fractions and Mixed Numbers: Learn how to compare fractions that are greater than one.
- Comparing More Than Two Fractions: Extend the techniques to compare multiple fractions simultaneously.
- Fraction Operations: Practice addition, subtraction, multiplication, and division of fractions to build a stronger foundation in fraction arithmetic.
Conclusion: Mastering the Art of Fraction Comparison
Determining whether 2/3 is bigger than 1/4 is a stepping stone to mastering fraction comparison. This seemingly simple question unlocks a world of mathematical understanding and problem-solving skills. Through visual representation, equivalent fractions, decimal conversions, and cross-multiplication, we’ve established that 2/3 is indeed greater than 1/4. Remember that choosing the most efficient method depends on the specific fractions involved and your personal preference. By understanding and applying these techniques, you'll gain confidence and proficiency in working with fractions, equipping you to tackle more complex mathematical challenges.
Latest Posts
Latest Posts
-
10 Characteristics Of A Civilization
Sep 20, 2025
-
22 Degrees Celsius To Kelvin
Sep 20, 2025
-
3a 7 2 3 A
Sep 20, 2025
-
What Should A Conclusion Include
Sep 20, 2025
-
Half Of 1 1 2 Teaspoons
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.