Is 3/4 Bigger Than 1/4
gasmanvison
Sep 23, 2025 · 5 min read
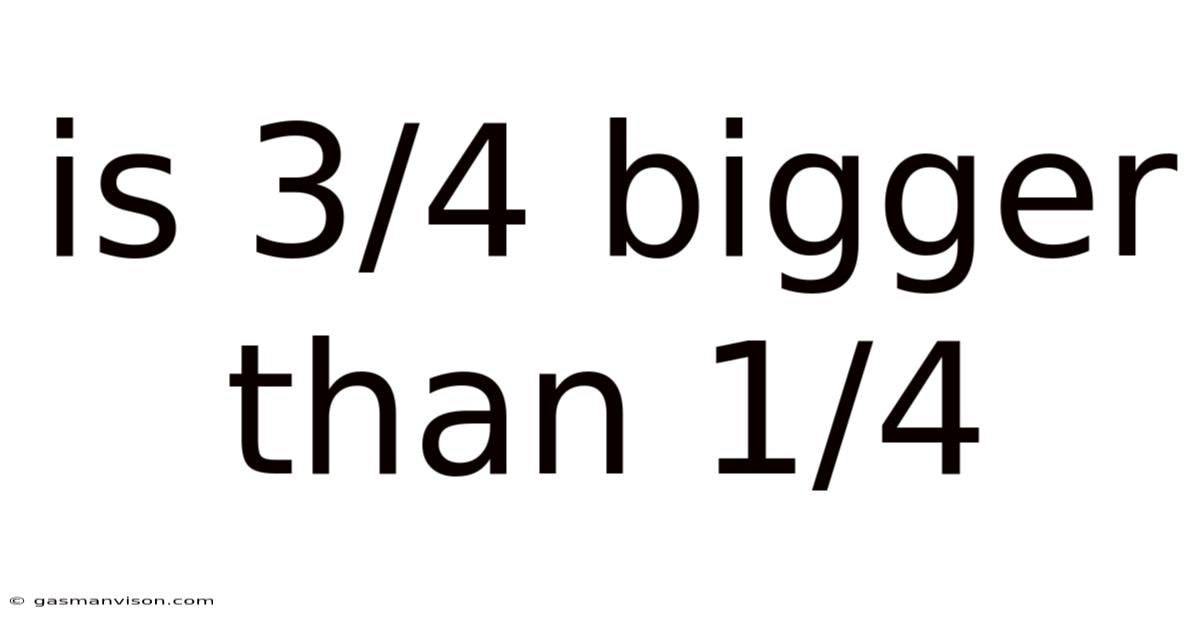
Table of Contents
Is 3/4 Bigger Than 1/4? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 3/4 bigger than 1/4?", opens the door to a comprehensive exploration of fractions, their representation, comparison methods, and practical applications. While the answer is a straightforward yes, understanding why 3/4 is larger than 1/4 requires a deeper understanding of fractional concepts. This article will delve into these concepts, providing various methods for comparing fractions and highlighting their importance in everyday life and advanced mathematics.
Understanding Fractions: The Building Blocks
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator 4 means the whole is divided into four equal parts, and the numerator 3 indicates we are considering three of those parts.
Visualizing Fractions: The Power of Representation
Visual aids are incredibly helpful in understanding fractions. Imagine a pizza cut into four equal slices. 1/4 represents one slice, while 3/4 represents three slices. This visual immediately demonstrates that 3/4 is larger than 1/4. We can use various visual aids like pie charts, bar models, and number lines to effectively represent and compare fractions. This visual approach is especially beneficial for beginners grasping the fundamental concepts of fractions.
Comparing Fractions: Methods and Strategies
There are several ways to compare fractions, each with its advantages depending on the complexity of the fractions involved.
1. Visual Comparison: As demonstrated with the pizza example, visual representation is the most intuitive method for comparing simple fractions. This approach works well for smaller denominators and readily allows for a quick understanding of the relative sizes.
2. Common Denominator Method: This is a powerful and widely used technique. To compare fractions with different denominators, we find a common denominator – a number that is a multiple of both denominators. Then, we convert both fractions to equivalent fractions with the common denominator and compare the numerators.
Let's compare 3/4 and 1/4 using this method: Both fractions already have a common denominator of 4. Since 3 > 1, we conclude that 3/4 > 1/4.
Let's try comparing 2/3 and 3/5. The least common denominator is 15. We convert 2/3 to 10/15 and 3/5 to 9/15. Since 10 > 9, we determine that 2/3 > 3/5.
3. Cross-Multiplication Method: This method is particularly efficient for comparing fractions without finding a common denominator. We cross-multiply the numerators and denominators and compare the products.
To compare 3/4 and 1/4:
- 3 x 4 = 12
- 1 x 4 = 4
Since 12 > 4, we conclude that 3/4 > 1/4.
For 2/3 and 3/5:
- 2 x 5 = 10
- 3 x 3 = 9
Since 10 > 9, we conclude that 2/3 > 3/5.
4. Decimal Conversion: Converting fractions to decimals provides another method for comparison. We divide the numerator by the denominator to obtain the decimal equivalent.
3/4 = 0.75 1/4 = 0.25
Since 0.75 > 0.25, we confirm that 3/4 > 1/4. This method is particularly useful when dealing with fractions that are difficult to compare using other methods.
Beyond Simple Comparison: Applications of Fractions
The ability to compare fractions is fundamental to numerous mathematical concepts and real-world applications.
-
Measurement: Fractions are essential in measuring quantities. Comparing fractions helps us determine which measurement is larger or smaller. For instance, comparing the length of two pieces of wood or the amount of liquid in two containers.
-
Cooking and Baking: Recipes often use fractions to specify ingredient quantities. Understanding fraction comparison ensures accurate measurements and successful outcomes.
-
Finance: Fractions play a vital role in finance, representing parts of a whole, such as shares of stock or portions of a budget. Comparing fractions helps in making informed financial decisions.
-
Data Analysis: Fractions and their comparison are fundamental in analyzing and interpreting data, such as in calculating percentages and proportions.
-
Geometry and Algebra: Fractions form the basis of many geometric and algebraic concepts, enabling us to solve equations, calculate areas and volumes, and understand ratios and proportions.
Advanced Fraction Concepts:
Beyond basic comparison, understanding more advanced fraction concepts like improper fractions (where the numerator is greater than or equal to the denominator), mixed numbers (a combination of a whole number and a fraction), and operations with fractions (addition, subtraction, multiplication, and division) are critical for mastering fractions and their applications in higher-level mathematics. These concepts build upon the foundational understanding of fraction comparison.
Conclusion: The Importance of Mastering Fractions
The question "Is 3/4 bigger than 1/4?" might seem trivial at first glance. However, the answer and the methods used to arrive at it underscore the crucial role fractions play in mathematics and everyday life. Mastering fraction comparison, along with other fraction operations, is essential for success in various academic pursuits and practical applications. By utilizing visual representations, common denominator methods, cross-multiplication, or decimal conversion, we can confidently compare fractions and make informed decisions based on fractional values. The ability to confidently navigate the world of fractions opens doors to a deeper understanding of mathematics and its impact on our world. The seemingly simple comparison of 3/4 and 1/4 serves as a gateway to a richer understanding of the power and versatility of fractions.
Latest Posts
Latest Posts
-
What Is Dippers Real Name
Sep 23, 2025
-
100mcg Is How Many Mg
Sep 23, 2025
-
Can A Ray Be Measured
Sep 23, 2025
-
Moderate Vs Liberal Vs Conservative
Sep 23, 2025
-
Financial Algebra Workbook Answer Key
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.