Is 5/6 Less Than 1/2
gasmanvison
Sep 22, 2025 · 5 min read
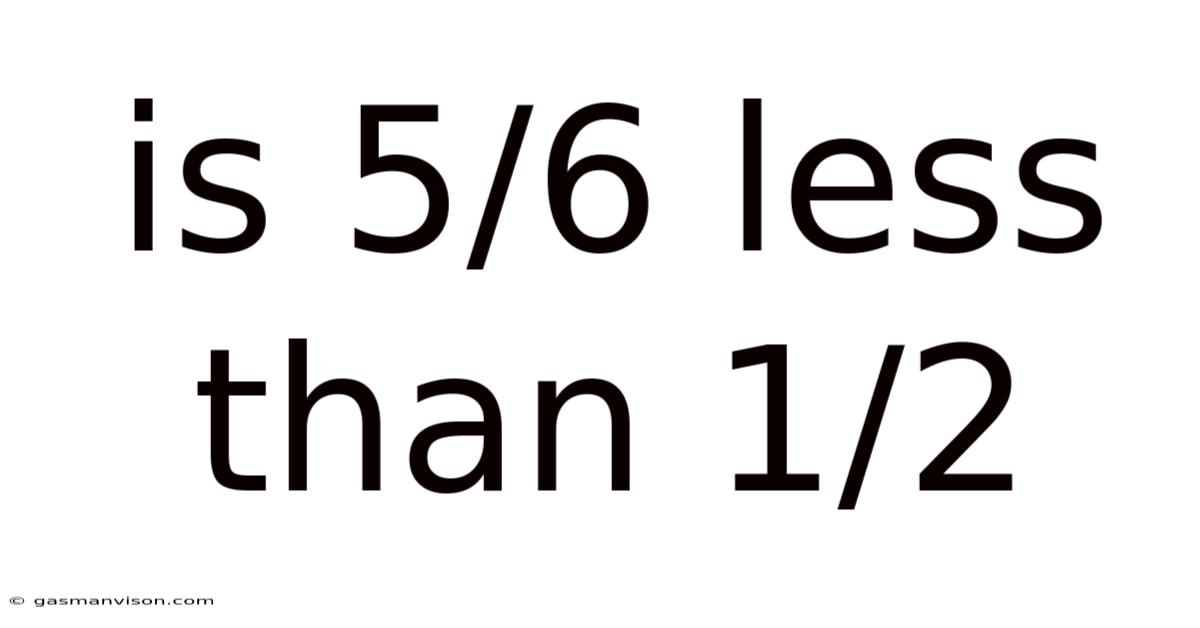
Table of Contents
Is 5/6 Less Than 1/2? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 5/6 less than 1/2?", opens the door to a fascinating exploration of fractions, their representation, and various methods for comparing them. While the answer might seem immediately obvious to some, understanding the underlying principles is crucial for developing a strong foundation in mathematics and for anyone working with data or needing to analyze proportions. This article will not only answer the question definitively but also equip you with the tools to compare any two fractions confidently. We'll explore multiple approaches, ensuring you grasp the concept thoroughly and can apply it in various contexts.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 1/2, the numerator is 1, and the denominator is 2, meaning you have one out of two equal parts.
Visualizing the Comparison: The Power of Representation
One of the most intuitive ways to compare fractions is through visualization. Imagine a pizza cut into six equal slices (representing the denominator of 5/6). If you have five slices (the numerator), you have a significant portion of the pizza. Now, imagine another pizza cut into only two equal slices (representing the denominator of 1/2). If you have only one slice, you have considerably less pizza than in the first scenario. This visual representation clearly shows that 5/6 is much larger than 1/2.
Method 1: Finding a Common Denominator
A more formal and mathematically rigorous approach involves finding a common denominator for both fractions. This means finding a number that is a multiple of both denominators (6 and 2). The least common multiple (LCM) of 6 and 2 is 6.
-
Converting 5/6: This fraction already has the common denominator, so it remains 5/6.
-
Converting 1/2: To convert 1/2 to have a denominator of 6, we multiply both the numerator and the denominator by 3: (1 * 3) / (2 * 3) = 3/6
Now, we can easily compare the two fractions: 5/6 and 3/6. Since 5 > 3, we can conclude that 5/6 > 1/2. Therefore, 5/6 is not less than 1/2; it's greater.
Method 2: Converting to Decimals
Another effective method involves converting both fractions to their decimal equivalents. This approach is particularly useful when dealing with more complex fractions or when you need a numerical comparison for calculations.
-
Converting 5/6 to a decimal: 5 ÷ 6 ≈ 0.833
-
Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
Comparing the decimal equivalents, 0.833 > 0.5, confirming that 5/6 > 1/2.
Method 3: Using Cross-Multiplication
Cross-multiplication provides a powerful algebraic technique for comparing fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and vice versa. Compare the resulting products.
-
Cross-multiplying 5/6 and 1/2:
- 5 * 2 = 10
- 6 * 1 = 6
Since 10 > 6, the fraction with the larger product (5/6) is the larger fraction. Therefore, 5/6 > 1/2.
Method 4: Comparing to Benchmark Fractions
A helpful strategy, especially for quick estimations, is to compare fractions to benchmark fractions like 0, 1/2, and 1. Since 5/6 is clearly closer to 1 than to 1/2, and 1/2 is exactly halfway between 0 and 1, it's evident that 5/6 is greater than 1/2. This method relies on intuition and a good understanding of fraction magnitudes.
Addressing Potential Misconceptions
A common misconception arises from focusing solely on the numerators. Some might mistakenly assume that because 5 > 1, 5/6 must be greater than 1/2. However, the denominators play a crucial role. The denominator indicates the size of the parts, and a smaller denominator means larger parts. Therefore, comparing numerators directly without considering the denominators can lead to inaccurate conclusions.
Applying Fraction Comparison in Real-World Scenarios
Understanding fraction comparison extends far beyond the realm of theoretical mathematics. It finds practical applications in diverse fields:
-
Cooking and Baking: Scaling recipes accurately often requires comparing and adjusting fractional amounts of ingredients.
-
Construction and Engineering: Precise measurements and calculations involving fractions are critical in construction projects to ensure structural integrity and accuracy.
-
Finance and Budgeting: Managing budgets and calculating percentages involves working with fractions and proportions.
-
Data Analysis: Interpreting data often involves analyzing proportions and percentages, which rely on a solid understanding of fractions.
-
Probability and Statistics: Calculating probabilities and interpreting statistical data often involves working with fractions and their comparisons.
Beyond the Basics: Expanding Your Fraction Knowledge
While this article focuses on comparing 5/6 and 1/2, the principles discussed apply to comparing any two fractions. To further enhance your understanding, consider exploring these related concepts:
-
Simplifying Fractions: Reducing fractions to their simplest form makes comparisons easier. For example, simplifying 6/12 to 1/2 makes the comparison to other fractions much simpler.
-
Improper Fractions and Mixed Numbers: Understanding how to convert between improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction) is crucial for more complex fraction operations.
-
Adding, Subtracting, Multiplying, and Dividing Fractions: Mastering these fundamental operations is essential for advanced fraction manipulations.
Conclusion: Mastering Fraction Comparison for Mathematical Fluency
The question, "Is 5/6 less than 1/2?", serves as an excellent starting point for understanding the importance of comparing fractions accurately. By mastering different methods – finding common denominators, converting to decimals, cross-multiplying, and comparing to benchmark fractions – you develop a robust mathematical skill set applicable to various real-world scenarios. Remember, focusing solely on numerators is insufficient; the denominators hold equal weight in determining the relative magnitude of fractions. With practice and a solid understanding of the underlying principles, you can confidently compare any two fractions and confidently navigate numerical problems involving proportions and ratios. This fundamental understanding forms the cornerstone of advanced mathematical concepts and provides a crucial skillset for numerous disciplines.
Latest Posts
Latest Posts
-
Maletas Ser Pasajero
Sep 22, 2025
-
Group 6a On Periodic Table
Sep 22, 2025
-
Fly Like The Wind Meaning
Sep 22, 2025
-
31 Billion In Scientific Notation
Sep 22, 2025
-
How Much Is 3 Nickels
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 5/6 Less Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.