Is 7/8 Bigger Than 3/4
gasmanvison
Sep 03, 2025 · 5 min read
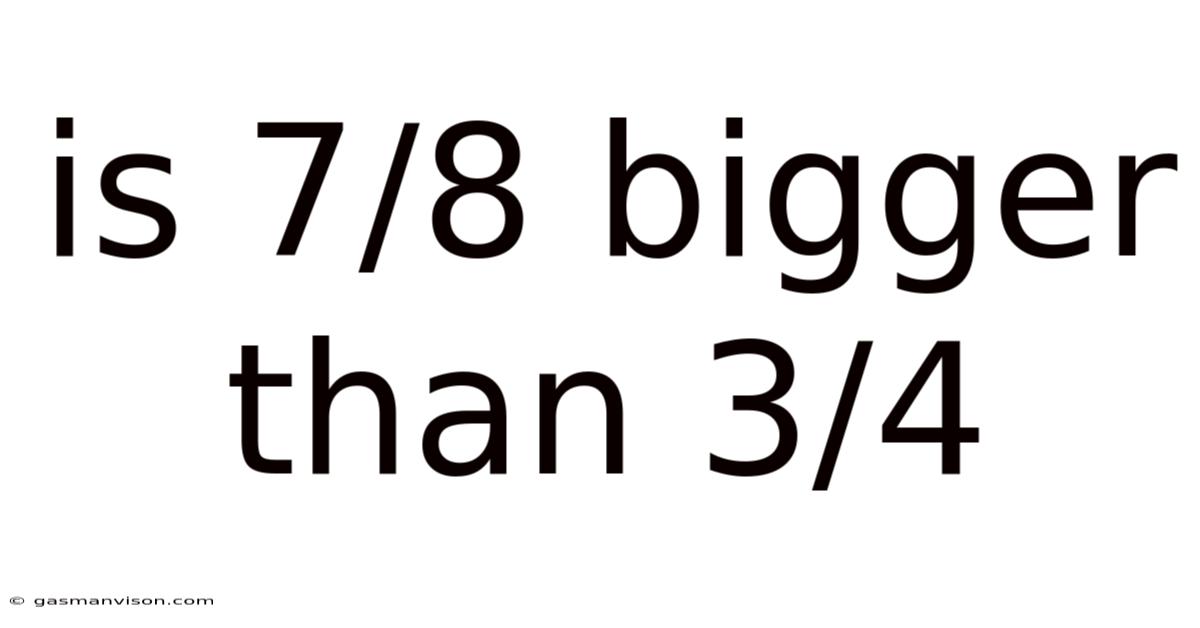
Table of Contents
Is 7/8 Bigger Than 3/4? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 7/8 bigger than 3/4?", opens a door to a broader understanding of fractions, a fundamental concept in mathematics. While the answer might seem obvious to some, a thorough exploration of this problem provides a valuable opportunity to reinforce core mathematical principles and develop effective strategies for comparing fractions. This article will not only answer the question directly but also equip you with the tools to confidently compare any two fractions. We'll delve into various methods, from visual representations to numerical calculations, ensuring a comprehensive understanding of the subject.
Meta Description: Learn how to compare fractions effectively! This in-depth guide explores different methods to determine if 7/8 is bigger than 3/4, covering visual aids, common denominators, decimal conversions, and more. Master fraction comparison with clear explanations and practical examples.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For instance, in the fraction 7/8, 7 is the numerator and 8 is the denominator. This means we have 7 out of 8 equal parts of a whole.
Method 1: Visual Representation
A visual approach can be incredibly helpful, especially when dealing with simpler fractions. Imagine two identical pizzas.
- Pizza 1: Cut into 8 equal slices, with 7 slices remaining (representing 7/8).
- Pizza 2: Cut into 4 equal slices, with 3 slices remaining (representing 3/4).
By visually comparing the remaining slices, it's clear that the 7/8 pizza has more remaining slices than the 3/4 pizza. This visual comparison confirms that 7/8 is indeed greater than 3/4. This method is particularly useful for beginners and helps build an intuitive understanding of fraction comparison.
Method 2: Finding a Common Denominator
This is a more formal and widely applicable method. The core idea is to rewrite the fractions so they have the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 7/8 and 3/4, we look for the least common multiple (LCM) of 8 and 4. The LCM of 8 and 4 is 8.
- 7/8: This fraction already has a denominator of 8, so it remains unchanged.
- 3/4: To change the denominator to 8, we multiply both the numerator and denominator by 2: (3 x 2) / (4 x 2) = 6/8
Now we can compare 7/8 and 6/8. Since 7 > 6, we conclude that 7/8 > 3/4.
Method 3: Converting to Decimals
Another effective method involves converting the fractions to decimals. This approach is particularly useful when dealing with more complex fractions or when needing a precise numerical comparison.
- 7/8: Divide 7 by 8: 7 ÷ 8 = 0.875
- 3/4: Divide 3 by 4: 3 ÷ 4 = 0.75
Comparing the decimal values, 0.875 > 0.75, confirming that 7/8 is greater than 3/4. This method provides a clear numerical representation that's easy to interpret. It's particularly helpful when using calculators or computer software for fraction comparisons.
Method 4: Cross-Multiplication
This method offers a quick and efficient way to compare fractions without finding a common denominator. Cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction (7) by the denominator of the second fraction (4): 7 x 4 = 28
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (8): 3 x 8 = 24
Since 28 > 24, we conclude that 7/8 > 3/4. This method is concise and avoids the need for finding the LCM, making it a time-saving technique for experienced users. However, it’s crucial to understand the underlying mathematical reasoning to apply it correctly.
Expanding the Understanding: Comparing Fractions with Different Numerators and Denominators
The principles outlined above can be applied to compare any two fractions, regardless of their numerators and denominators. Let's consider a more complex example: Comparing 5/6 and 7/9.
Method 1: Common Denominator: The LCM of 6 and 9 is 18.
- 5/6 = (5 x 3) / (6 x 3) = 15/18
- 7/9 = (7 x 2) / (9 x 2) = 14/18
Since 15 > 14, 5/6 > 7/9.
Method 2: Decimal Conversion:
- 5/6 ≈ 0.833
- 7/9 ≈ 0.778
Again, 5/6 > 7/9.
Method 3: Cross-Multiplication:
- 5 x 9 = 45
- 7 x 6 = 42
Since 45 > 42, 5/6 > 7/9.
Beyond the Basics: Improper Fractions and Mixed Numbers
The methods discussed so far apply equally to improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a fraction). To compare, it's often helpful to convert improper fractions to mixed numbers or vice-versa for easier comparison.
For instance, comparing 11/4 and 2 3/8:
Convert 11/4 to a mixed number: 2 3/4. Now, comparing 2 3/4 and 2 3/8 is straightforward; 2 3/4 > 2 3/8.
Practical Applications of Fraction Comparison
Understanding fraction comparison is crucial in various real-world scenarios:
- Cooking and Baking: Following recipes often requires precise measurements, demanding a solid understanding of fraction comparison to ensure accurate ingredient proportions.
- Construction and Engineering: Precise measurements and calculations are critical in these fields, where understanding fraction relationships is paramount.
- Finance: Calculating interest rates, proportions of investments, and other financial computations frequently involve fraction comparisons.
- Data Analysis: Understanding proportions and ratios in data often relies on comparing fractions to draw meaningful conclusions.
Conclusion
Determining whether 7/8 is bigger than 3/4 is more than just a simple mathematical problem; it's a gateway to understanding fundamental concepts of fractions and their comparison. This article explored various methods – visual representation, common denominators, decimal conversion, and cross-multiplication – each offering a unique approach to effectively comparing fractions. By mastering these techniques, you’ll develop a strong foundation in mathematics and equip yourself with valuable skills applicable across numerous fields. Remember to choose the method that best suits your understanding and the complexity of the fractions involved. Practice makes perfect; so, try comparing different fractions using these techniques to solidify your understanding.
Latest Posts
Latest Posts
-
Number Of Protons In Boron
Sep 03, 2025
-
Scientific Theory Versus Scientific Law
Sep 03, 2025
-
Population Of Greater Los Angeles
Sep 03, 2025
-
Is Water Renewable Or Nonrenewable
Sep 03, 2025
-
Time Flies Like An Arrow
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about Is 7/8 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.