Log Base 3 Of 3
gasmanvison
Sep 20, 2025 · 5 min read
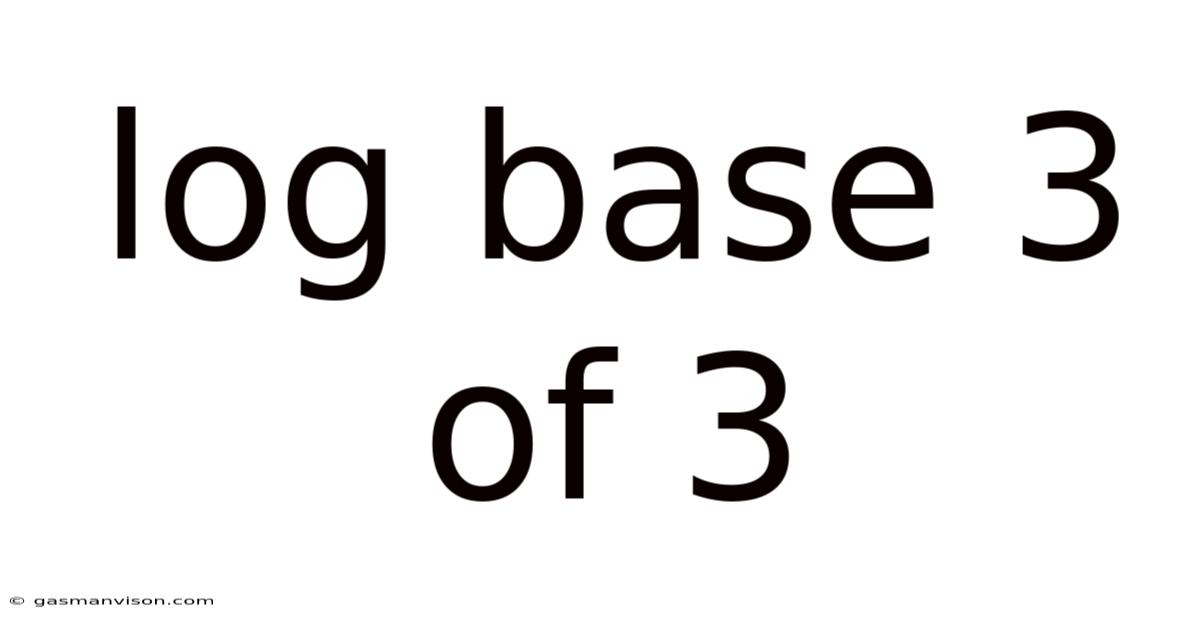
Table of Contents
Decoding the Simplicity: A Deep Dive into Log₃3
This article explores the seemingly simple mathematical expression, log₃3. While the answer might appear immediately obvious to many, delving deeper reveals fundamental concepts within logarithmic functions, their applications, and connections to exponential functions. Understanding log₃3 unlocks a broader comprehension of logarithms and their role in various fields, from solving complex equations to modeling real-world phenomena.
What is a Logarithm? A Quick Refresher
Before we tackle log₃3, let's briefly revisit the definition of a logarithm. A logarithm answers the question: "To what power must we raise a base to obtain a given number?" In the general form, logₐb = x, this translates to aˣ = b. Here:
- a is the base of the logarithm (must be positive and not equal to 1).
- b is the argument (must be positive).
- x is the exponent or logarithm.
Therefore, a logarithm is essentially the inverse function of an exponential function. This inverse relationship is crucial for understanding and manipulating logarithmic expressions.
Understanding log₃3
Now, let's focus on log₃3. Using the general form, we have:
logₐb = x => aˣ = b
In our case, a = 3 (the base) and b = 3 (the argument). So, the equation becomes:
log₃3 = x => 3ˣ = 3
The question is: "To what power must we raise 3 to get 3?" The answer is clearly 1. Therefore:
log₃3 = 1
This simple equation demonstrates a fundamental property of logarithms: the logarithm of a number to the same base is always 1. This applies to any positive base (excluding 1). For instance:
- log₂2 = 1
- log₁₀10 = 1
- logₑe = 1 (where 'e' is the Euler's number, approximately 2.718)
The Inverse Relationship between Logarithms and Exponentials
The relationship between logarithms and exponentials is deeply intertwined. They are inverse functions, meaning they "undo" each other. This is easily demonstrated with log₃3:
- We know that log₃3 = 1.
- If we apply the exponential function with base 3 to both sides, we get: 3^(log₃3) = 3¹
- This simplifies to 3¹ = 3, which is true.
Conversely, if we start with 3¹ = 3 and take the base-3 logarithm of both sides, we get: log₃(3¹) = log₃3 This simplifies to 1 = 1, again confirming the inverse relationship.
Applications of Logarithms: Beyond the Basics
While log₃3 might seem like a trivial example, the underlying principles have far-reaching applications across numerous fields:
1. Solving Exponential Equations:
Logarithms are indispensable tools for solving exponential equations. Consider an equation like 3ˣ = 27. To solve for x, we can take the base-3 logarithm of both sides:
log₃(3ˣ) = log₃27
Using the logarithm power rule (logₐ(bˣ) = x logₐb), we get:
x log₃3 = log₃27
Since log₃3 = 1, this simplifies to:
x = log₃27
Recognizing that 27 = 3³, we find:
x = log₃(3³) = 3 log₃3 = 3 * 1 = 3
Therefore, x = 3. This demonstrates how logarithms effectively transform exponential equations into simpler linear equations.
2. Scientific and Engineering Applications:
Logarithms are extensively used in various scientific and engineering disciplines:
- Chemistry: pH calculations (measuring acidity/alkalinity) utilize the base-10 logarithm.
- Physics: Measuring sound intensity (decibels) and earthquake magnitudes (Richter scale) rely on logarithmic scales.
- Computer Science: Computational complexity analysis often employs logarithmic notation to describe algorithm efficiency.
- Finance: Compound interest calculations and modeling population growth often involve exponential functions and their logarithmic counterparts.
3. Data Analysis and Visualization:
Logarithmic scales are invaluable for visualizing data spanning vast ranges. When dealing with data that covers several orders of magnitude (e.g., astronomical distances or microscopic sizes), a logarithmic scale compresses the range making patterns and trends easier to discern.
Expanding on Logarithmic Properties: Relevance to log₃3
Understanding log₃3 also helps illuminate various logarithmic properties. Let's review some key properties and see how they relate to our example:
- Product Rule: logₐ(xy) = logₐx + logₐy
- Quotient Rule: logₐ(x/y) = logₐx - logₐy
- Power Rule: logₐ(xⁿ) = n logₐx
- Change of Base Rule: logₐx = (logₓx) / (logₓa)
These properties, while not directly used in the simplification of log₃3, are fundamental to manipulating more complex logarithmic expressions. For instance, the power rule explains why log₃(3³) = 3, which is crucial for solving many exponential equations. The change of base rule allows us to convert logarithms between different bases, a powerful tool when dealing with calculators that might only have base-10 or base-e logarithms.
Exploring Beyond Base 3: Generalizing the Concept
The simplicity of log₃3 allows for a broader understanding of logarithmic functions. The core principle – the logarithm of a number to the same base always equals 1 – remains consistent regardless of the base. This uniformity underscores the elegance and power of logarithmic functions.
Conclusion: The Significance of Simplicity
While log₃3 might seem like a basic mathematical concept, its understanding is crucial for grasping the fundamental principles of logarithmic functions. This seemingly simple expression serves as a gateway to understanding the inverse relationship with exponential functions, unlocking the power of logarithms in solving complex equations and their widespread applications across diverse scientific, engineering, and data analysis fields. The simplicity of log₃3 = 1 shouldn't be underestimated; it's a cornerstone of logarithmic mathematics, providing a solid foundation for more advanced concepts. By thoroughly understanding this fundamental expression, we unlock a deeper appreciation for the broader world of logarithmic calculations and their significant role in problem-solving and scientific exploration.
Latest Posts
Latest Posts
-
Examples Of Absorption In Waves
Sep 20, 2025
-
Why Does Rebreathing Simulate Hypoventilation
Sep 20, 2025
-
200 Degree C To F
Sep 20, 2025
-
What Is Achs Blood Sugars
Sep 20, 2025
-
What Is 5 Of 700
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Log Base 3 Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.