_ Of 15 Is 6
gasmanvison
Sep 12, 2025 · 5 min read
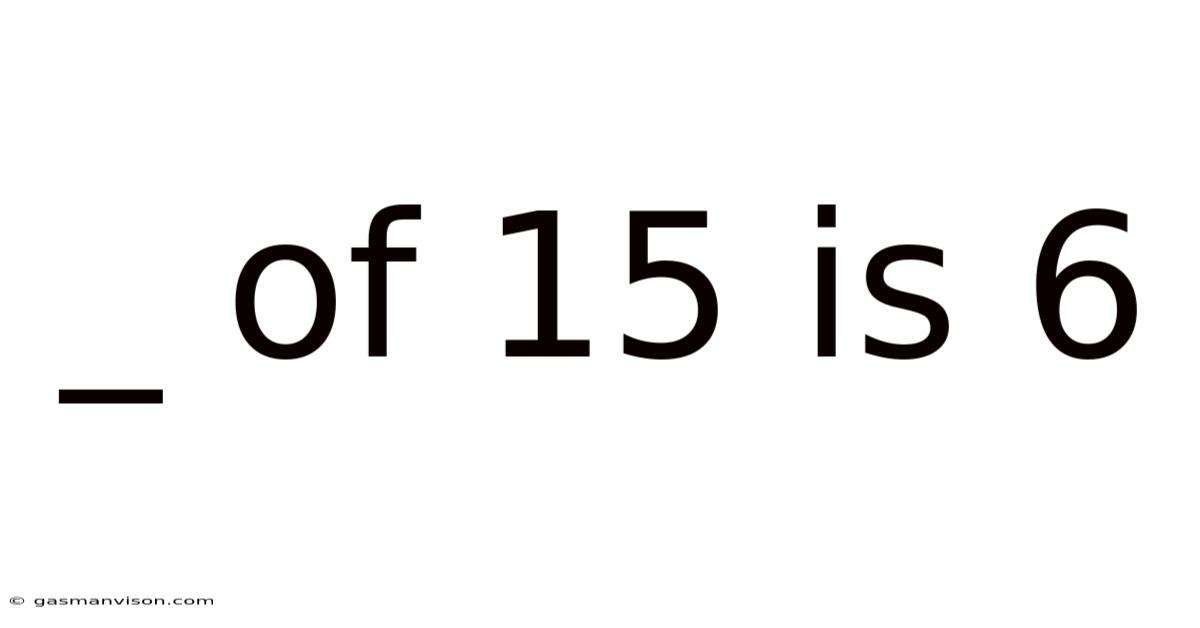
Table of Contents
Decoding "What Fraction of 15 is 6?": A Deep Dive into Fractions, Ratios, and Percentages
This seemingly simple question, "What fraction of 15 is 6?", opens a door to a world of mathematical concepts that are crucial for everyday life, from baking and budgeting to understanding data and statistics. This article will explore this problem in detail, explaining not just the answer but the underlying principles of fractions, ratios, and percentages, providing you with a solid foundation to tackle similar problems with confidence. This detailed explanation will enhance your understanding of fundamental mathematical concepts and improve your problem-solving skills.
Understanding the Problem: Fractions, Ratios, and Proportions
The question "What fraction of 15 is 6?" essentially asks us to express the relationship between 6 and 15 as a fraction. A fraction represents a part of a whole. In this case, the whole is 15, and the part is 6. We can also view this relationship as a ratio – a comparison of two quantities. The ratio of 6 to 15 is written as 6:15 or 6/15. Finally, understanding this relationship allows us to calculate the percentage of 15 that 6 represents.
Finding the Fraction: The Simple Solution
The most straightforward way to find the fraction is to write the part (6) as the numerator and the whole (15) as the denominator:
6/15
This fraction, however, can be simplified. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 6 and 15 is 3. Dividing both the numerator and the denominator by 3 gives us:
2/5
Therefore, 6 is two-fifths of 15.
Expanding Our Understanding: Ratios and Proportions
The problem can also be approached using the concept of ratios and proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve for the unknown fraction:
x/15 = 6/15
Here, 'x' represents the fraction we're trying to find. To solve for x, we can cross-multiply:
15x = 6 * 15
15x = 90
x = 90/15
x = 6
This confirms that 6 is indeed 6/15, or 2/5, of 15. While this approach might seem redundant in this specific problem, it becomes invaluable when dealing with more complex proportions where one or more values are unknown.
Converting to Percentage: Expressing the Relationship as a Percentage
Converting the fraction 2/5 to a percentage involves multiplying the fraction by 100%:
(2/5) * 100% = 40%
Therefore, 6 represents 40% of 15. This percentage representation is particularly useful for comparisons and interpretations in various contexts.
Real-World Applications: Putting the Knowledge into Practice
The concepts we've explored are far from abstract mathematical exercises. They have wide-ranging practical applications:
-
Baking: A recipe calls for 15 cups of flour, and you only want to make 6 cups of the recipe's yield. Understanding fractions will help you adjust the quantities of other ingredients accordingly. You'd use 2/5 or 40% of the original quantity of each ingredient.
-
Shopping: A shirt is originally priced at $15, and it's on sale for $6. Knowing that this represents a 40% discount can help you compare prices more effectively.
-
Data Analysis: In data analysis, fractions and percentages are commonly used to express proportions and trends. For example, understanding the fraction of a certain demographic group responding positively to a survey provides valuable insights for market research.
-
Finance: Calculating interest rates, loan repayments, and investment returns all involve the use of fractions and percentages.
-
Construction: Measurements and proportions in blueprints rely heavily on fractions and ratios to ensure accuracy and scale.
Beyond the Basics: Tackling More Complex Problems
While the problem "What fraction of 15 is 6?" is relatively straightforward, the principles involved can be extended to more complex scenarios. Consider these examples:
-
Finding the whole: If 40% of a number is 6, what is the number? This involves working backward from the percentage and using proportion to find the whole.
-
Comparing fractions: Comparing fractions with different denominators requires finding a common denominator or converting them to decimals or percentages.
-
Solving word problems: Real-world problems often involve interpreting textual information and translating it into mathematical expressions involving fractions and ratios.
Mastering Fractions, Ratios, and Percentages: A Continuous Journey
Mastering fractions, ratios, and percentages is a crucial step in developing strong mathematical skills. This understanding is not just confined to academic settings; it’s a fundamental tool for navigating everyday situations effectively. Regular practice and applying these concepts in various contexts will reinforce your understanding and build your confidence in solving more complex mathematical problems.
Strategies for Further Learning and Practice
To solidify your understanding and further develop your skills, consider these strategies:
-
Practice regularly: Solve a variety of problems involving fractions, ratios, and percentages. Start with simple examples and gradually increase the complexity.
-
Use visual aids: Diagrams, charts, and other visual representations can be helpful in understanding and visualizing fractions and ratios.
-
Seek additional resources: Numerous online resources, textbooks, and tutorials are available to help you learn more about these concepts.
-
Work with others: Collaborating with peers or seeking help from a tutor can enhance your understanding and provide different perspectives.
-
Apply your knowledge: Look for opportunities to apply your knowledge of fractions, ratios, and percentages in real-world situations.
By understanding and applying the principles discussed in this article, you'll not only be able to confidently answer the question "What fraction of 15 is 6?" but also tackle more complex mathematical problems, enhancing your problem-solving skills and empowering you in various aspects of your life. Remember, mathematical proficiency is a skill that develops over time with consistent effort and practice.
Latest Posts
Latest Posts
-
Scientific Name Of The Cat
Sep 13, 2025
-
How Many Inches Is 5 9
Sep 13, 2025
-
Left Shoulder Pain Icd 10
Sep 13, 2025
-
When Does Dna Replication Occur
Sep 13, 2025
-
Usa Country Code Phone 001
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about _ Of 15 Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.