Solve 2x 5 27 X
gasmanvison
Sep 18, 2025 · 5 min read
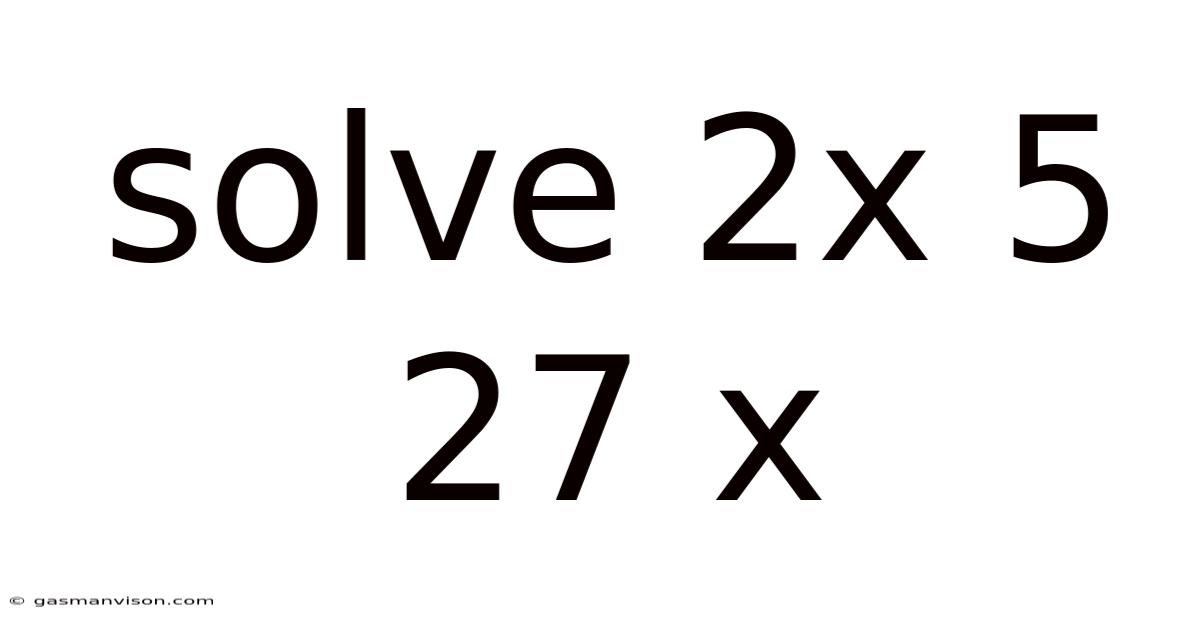
Table of Contents
Solving the Equation: 2x + 5 = 27x – A Comprehensive Guide
This article provides a comprehensive guide on how to solve the algebraic equation 2x + 5 = 27x, covering various approaches and explaining the underlying mathematical principles. We will delve into the steps involved, explain the reasoning behind each step, and offer tips for solving similar equations effectively. This guide is aimed at both beginners who are just starting to learn algebra and those who need a refresher on solving linear equations. Understanding how to solve this type of equation is fundamental for further advancements in mathematics and related fields.
Understanding the Equation:
The equation 2x + 5 = 27x is a linear equation because the highest power of the variable 'x' is 1. Solving this equation means finding the value of 'x' that makes the equation true. In simpler terms, we're looking for the number that, when substituted for 'x', makes both sides of the equation equal. This process involves manipulating the equation using algebraic rules to isolate 'x' on one side of the equation.
Method 1: Isolating the Variable 'x'
The most straightforward method involves isolating the variable 'x' on one side of the equation. This is achieved by performing the same operation on both sides of the equation to maintain balance. Let's break down the steps:
-
Subtract 2x from both sides: Our goal is to group all terms containing 'x' together. Subtracting 2x from both sides eliminates '2x' from the left side:
2x + 5 - 2x = 27x - 2x
This simplifies to:
5 = 25x
-
Divide both sides by 25: To isolate 'x', we need to divide both sides of the equation by the coefficient of 'x', which is 25:
5 / 25 = 25x / 25
This simplifies to:
1/5 = x
Therefore, the solution to the equation 2x + 5 = 27x is x = 1/5 or x = 0.2.
Method 2: Using the Properties of Equality
This method emphasizes the properties of equality – the rules that allow us to manipulate equations without changing their solutions. The key properties used here are the addition property of equality and the multiplication property of equality.
-
Addition Property of Equality: This property states that adding the same number to both sides of an equation maintains the equality. We'll use this to move the '2x' term:
2x + 5 = 27x
Subtract 2x from both sides:
2x + 5 - 2x = 27x - 2x
5 = 25x
-
Multiplication Property of Equality: This property states that multiplying both sides of an equation by the same non-zero number maintains the equality. We'll use this to solve for 'x':
5 = 25x
Divide both sides by 25:
5/25 = 25x/25
1/5 = x
Again, the solution is x = 1/5 or x = 0.2.
Verification of the Solution:
It's crucial to verify the solution by substituting the value of 'x' back into the original equation:
2x + 5 = 27x
2(1/5) + 5 = 27(1/5)
2/5 + 5 = 27/5
Converting 5 to fifths (25/5):
2/5 + 25/5 = 27/5
27/5 = 27/5
Since both sides are equal, our solution x = 1/5 is correct.
Understanding the Concepts:
To fully grasp solving linear equations like this, it's essential to understand these key concepts:
- Variables: These are symbols, usually letters (like 'x'), that represent unknown quantities.
- Coefficients: These are the numbers multiplying the variables (e.g., 2 in 2x).
- Constants: These are numbers without variables (e.g., 5 in 2x + 5).
- Terms: These are individual parts of an equation separated by plus or minus signs (e.g., 2x, 5, and 27x).
- Equations: Statements indicating that two expressions are equal.
- Solving an equation: Finding the value(s) of the variable(s) that make the equation true.
Solving Similar Equations:
The steps outlined above can be applied to solve various similar linear equations. The key is to always maintain balance by performing the same operation on both sides of the equation. For example, consider the equation:
3x - 7 = 14x + 2
- Subtract 3x from both sides: -7 = 11x + 2
- Subtract 2 from both sides: -9 = 11x
- Divide both sides by 11: x = -9/11
Therefore, the solution to 3x - 7 = 14x + 2 is x = -9/11.
Advanced Techniques:
While the methods above are sufficient for this particular equation, more complex linear equations might require additional techniques such as:
- Combining like terms: Grouping terms with the same variable together before isolating the variable.
- Distributive property: Expanding expressions by multiplying a term by each term within parentheses.
- Factoring: Expressing an expression as a product of simpler expressions.
These advanced techniques are typically introduced in more advanced algebra courses.
Applications of Linear Equations:
Linear equations have wide-ranging applications across various fields, including:
- Physics: Calculating speed, distance, and time.
- Engineering: Designing structures and analyzing forces.
- Economics: Modeling supply and demand.
- Computer science: Developing algorithms and solving problems.
Conclusion:
Solving the equation 2x + 5 = 27x is a fundamental skill in algebra. By understanding the steps involved and the underlying mathematical principles, you can confidently solve various linear equations. Remember to always verify your solution by substituting it back into the original equation. Practice is key to mastering this skill, and with consistent effort, you'll become proficient in solving a wide range of algebraic problems. This foundation will serve you well as you progress to more complex mathematical concepts and their real-world applications. Understanding linear equations is a crucial stepping stone towards further mathematical exploration and success in various fields. Continue practicing and exploring different types of equations to build a strong mathematical foundation.
Latest Posts
Latest Posts
-
A Child Welfare Agency Includes
Sep 18, 2025
-
41 Degrees C To F
Sep 18, 2025
-
Distance Austin To Dallas Tx
Sep 18, 2025
-
17 Degrees C In Fahrenheit
Sep 18, 2025
-
Tu Las Manos Con Jabon
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Solve 2x 5 27 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.