Solve 3125 5 10 3x
gasmanvison
Sep 09, 2025 · 5 min read
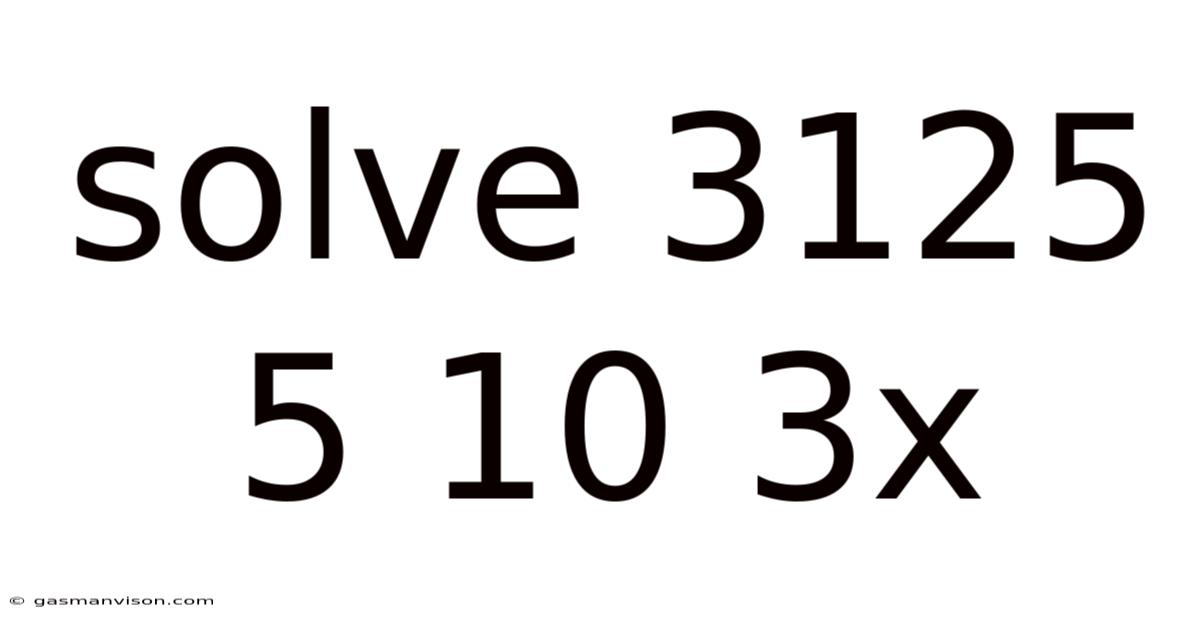
Table of Contents
Decoding the Mathematical Puzzle: Solving for x in 3125⁵¹⁰³ˣ
This article delves into the solution of the mathematical equation 3125⁵¹⁰³ˣ, exploring various approaches, demonstrating the steps involved, and explaining the underlying mathematical concepts. We'll break down the problem, examine different methods of solving it, and discuss the significance of understanding exponential and logarithmic functions in tackling such problems. The ultimate goal is not just to find the solution but to develop a comprehensive understanding of the process.
Understanding the Equation: A Breakdown
At first glance, the equation 3125⁵¹⁰³ˣ might seem daunting. However, by breaking it down, we can reveal its simpler components. The core of the equation lies in its exponential nature. We are dealing with a base (3125) raised to a power (5¹⁰³ˣ). This power itself contains a variable (x), making it an exponential equation that requires a specific approach to solve. The number 3125 is significant because it's a perfect power of 5 (5⁵ = 3125). This fact will play a crucial role in simplifying our solution.
Method 1: Utilizing Logarithmic Properties
One effective way to solve for 'x' in an exponential equation is by using logarithms. Logarithms are the inverse functions of exponentials, allowing us to bring down exponents as multipliers. Let's outline the steps:
-
Rewrite the equation: The equation can be written as: 5⁵⁵¹⁰³ˣ = some value (we'll determine this value later). This simplification is crucial because we've replaced the large number 3125 with its equivalent, 5⁵. This simplifies the equation and makes it easier to work with.
-
Apply the logarithm: Taking the logarithm of both sides of the equation allows us to simplify the exponent. We can use any base for the logarithm (common log, base-10, or natural log, base-e), but the choice of base might influence the complexity of the calculations. Let's use the natural logarithm (ln):
ln(5⁵⁵¹⁰³ˣ) = ln(some value)
-
Use logarithmic properties: Using the power rule of logarithms (log(aᵇ) = b*log(a)), we can bring down the exponent:
5¹⁰³ˣ * ln(5⁵) = ln(some value)
-
Simplify: We know ln(5⁵) = 5ln(5). Substituting this, we have:
5¹⁰³ˣ * 5ln(5) = ln(some value)
-
Isolate 'x': Now, we need to isolate 'x'. This involves dividing both sides by 5ln(5) and then potentially using further logarithmic properties or algebraic manipulation depending on the "some value" we obtain in step 1. The exact steps will vary depending on whether the equation is set equal to a specific number or another expression.
Method 2: Considering the "Some Value" Scenario
The above approach is incomplete because it doesn’t specify the “some value” that the expression equates to. If the equation is set to a known value, for example, 3125⁵¹⁰³ˣ = Y, the process would continue as follows:
-
Rewrite and Simplify: 5⁵⁵¹⁰³ˣ = Y
-
Take Logarithms: ln(5⁵⁵¹⁰³ˣ) = ln(Y)
-
Apply Log Rules: (5¹⁰³ˣ)(5ln5) = ln(Y)
-
Isolate the Exponential Term: 5¹⁰³ˣ = ln(Y) / (5ln5)
-
Take Logarithms Again: ln(5¹⁰³ˣ) = ln[ln(Y) / (5ln5)]
-
Apply Log Rules & Solve for x: (10³x)(ln5) = ln[ln(Y) / (5ln5)]
x = ln[ln(Y) / (5ln5)] / (10³ln5)
Method 3: Exploring Potential Simplifications & Special Cases
The equation's solvability heavily depends on the context in which it's presented. Are we looking for an integer solution? A real solution? Or a complex solution? Consider these possibilities:
-
If the equation is part of a larger problem: The context of the equation within a larger mathematical problem may provide clues or allow for simplifications. For instance, if the equation appears within a system of equations, it may be possible to use substitution or elimination techniques.
-
Numerical Methods: For more complex scenarios where analytical solutions are difficult to obtain, numerical methods such as iterative techniques (like the Newton-Raphson method) can be employed to approximate the value of 'x'. These methods involve making successive approximations to reach a solution within a specified tolerance.
-
Graphing Techniques: Graphing the function y = 3125⁵¹⁰³ˣ can help visually identify potential solutions for 'x', especially if the equation is set equal to a constant. Looking for x-intercepts (where y = 0) or the point where the graph intersects a horizontal line representing the constant value will reveal the solution(s).
Importance of Understanding Exponential and Logarithmic Functions
Solving equations like 3125⁵¹⁰³ˣ requires a solid understanding of exponential and logarithmic functions. Here's why:
-
Exponential growth and decay: Exponential functions model numerous real-world phenomena, from population growth to radioactive decay. Understanding their properties is crucial for analyzing and predicting these processes.
-
Inverse relationship: Logarithms are the inverse functions of exponentials. This inverse relationship is fundamental to solving exponential equations. They allow us to transform exponential expressions into linear ones, making them easier to manipulate algebraically.
-
Applications in various fields: Exponential and logarithmic functions have wide-ranging applications in diverse fields, including finance (compound interest), physics (radioactive decay), chemistry (reaction rates), and computer science (algorithm complexity).
Conclusion: A Multifaceted Approach
Solving 3125⁵¹⁰³ˣ involves a multifaceted approach combining algebraic manipulation, logarithmic properties, and potentially numerical or graphical methods. The exact solution hinges on the context of the equation, specifically the value to which it is equated. This article highlights the significance of understanding the fundamental principles of exponential and logarithmic functions, which are essential tools for solving a broad range of mathematical problems encountered in diverse scientific and engineering disciplines. Remember to always consider the context of the problem and choose the most appropriate method for finding a solution. The key takeaway is to break down the problem into manageable steps and utilize the appropriate mathematical tools to achieve the solution.
Latest Posts
Latest Posts
-
Entrench Is To Dislodge As
Sep 09, 2025
-
Before Changing Lanes You Must
Sep 09, 2025
-
Jane And Jill Collect Yoyos
Sep 09, 2025
-
Alpha Kappa Alpha Greek Goddess
Sep 09, 2025
-
Residual Nitrogen Is Defined As
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Solve 3125 5 10 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.