Solve E Mc2 For C
gasmanvison
Sep 18, 2025 · 6 min read
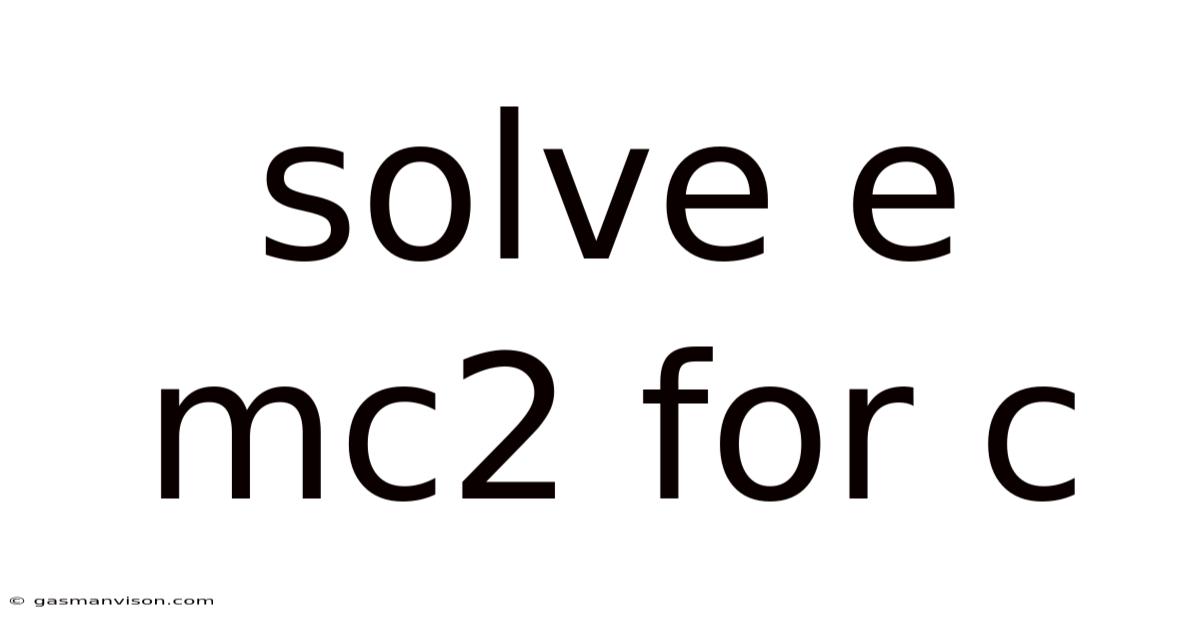
Table of Contents
Solving E=mc² for c: Unraveling the Speed of Light
Einstein's famous equation, E=mc², is a cornerstone of modern physics, elegantly linking energy (E) and mass (m) through the constant speed of light (c). While the equation is often presented as a statement of equivalence, it's also a powerful tool for calculating any of these three variables if the other two are known. This article will delve into the process of solving E=mc² for c, exploring the mathematical steps, the implications of the solution, and its significance in understanding the universe. We'll also examine related concepts and potential applications.
Understanding the Equation and its Components
Before diving into the solution, let's briefly review the meaning of each component in the equation:
-
E: Represents energy, typically measured in joules (J). Energy encompasses various forms, including kinetic energy (energy of motion), potential energy (stored energy), and rest energy (energy inherent to an object's mass).
-
m: Represents mass, usually measured in kilograms (kg). Mass is a measure of an object's inertia – its resistance to changes in motion. In the context of E=mc², we're dealing with relativistic mass, which increases with velocity.
-
c: Represents the speed of light in a vacuum, a fundamental constant approximately equal to 299,792,458 meters per second (m/s). This speed is incredibly fast and forms the upper limit for the speed of any object or information in the universe.
Solving for c: The Mathematical Steps
To solve E=mc² for c, we need to isolate c on one side of the equation using basic algebraic manipulation. Here's how:
-
Divide both sides by m: This removes the mass (m) from the right side of the equation, leaving only c². The equation becomes: E/m = c²
-
Take the square root of both sides: This eliminates the square on c, giving us the final solution for c: c = √(E/m)
This equation now allows us to calculate the speed of light (c) if we know the energy (E) and mass (m) of a system. It's crucial to remember that the units must be consistent (e.g., joules for energy and kilograms for mass) to obtain a result in meters per second for the speed of light. Using inconsistent units will lead to an incorrect answer.
Implications and Applications of the Solution
The ability to solve for c has far-reaching implications across various scientific fields:
-
Nuclear Physics: Nuclear reactions, such as fission and fusion, involve significant changes in mass. By measuring the energy released during these reactions and the change in mass, we can use the equation c = √(E/m) to verify the speed of light as a fundamental constant. The vast energy released in nuclear reactions is a direct consequence of the conversion of a small amount of mass into a large amount of energy, as dictated by E=mc².
-
Particle Physics: In particle accelerators, immense energies are used to create new particles. The equation provides a way to calculate the mass of newly discovered particles based on the energy involved in their creation. This has been instrumental in advancing our understanding of fundamental particles and forces.
-
Astrophysics: The equation plays a crucial role in understanding the energy production mechanisms within stars. Nuclear fusion reactions within stars convert mass into energy, which powers the star's luminosity and sustains its existence. This energy is radiated across the electromagnetic spectrum providing insight into stellar evolution.
-
Cosmology: On the grandest scales, E=mc² helps us understand the evolution of the universe. The equation allows us to explore the relationship between matter and energy density in the early universe and the implications for its expansion. The understanding of dark energy and dark matter also builds upon this fundamental concept.
-
Technological Advancements: While not a direct application, the underlying principles of E=mc² have indirectly driven advancements in various technologies, including nuclear power generation (though the efficiency isn't directly governed by this equation alone, the energy release is). The deeper understanding of energy-mass equivalence has spurred research and development in areas ranging from medical imaging (PET scans utilize annihilation radiation) to various industrial processes.
Beyond the Simple Equation: Relativistic Considerations
While the equation E=mc² is often simplified to represent rest energy (the energy associated with an object's mass at rest), the complete relativistic energy-momentum relation is more comprehensive:
E² = (pc)² + (mc²)²
Where:
- E: Total relativistic energy
- p: Momentum
- m: Rest mass
- c: Speed of light
This equation accounts for the kinetic energy of moving objects, showing that the total energy is the sum of the rest energy and the energy associated with momentum. When an object is at rest (p=0), this equation simplifies to the familiar E=mc². Solving for c in the full relativistic equation is significantly more complex and requires consideration of both energy and momentum.
Practical Examples and Calculations
Let's consider a few examples to illustrate how to solve for c using the simplified equation, E=mc²:
Example 1:
A small amount of mass, m = 1 kg, is entirely converted into energy. Calculate the speed of light using the energy released, E = 9 x 10¹⁶ J.
Solution:
c = √(E/m) = √(9 x 10¹⁶ J / 1 kg) ≈ 3 x 10⁸ m/s
This result accurately reflects the accepted value of the speed of light.
Example 2:
Imagine a hypothetical process where 0.001 kg of mass is converted into energy, resulting in E = 9 x 10¹³ J. Solve for c.
Solution:
c = √(E/m) = √(9 x 10¹³ J / 0.001 kg) ≈ 3 x 10⁸ m/s
Again, we obtain the approximate speed of light, confirming the consistency of the equation.
Addressing Common Misconceptions
Several misconceptions often surround E=mc²:
-
It doesn't mean anything can be converted into pure energy: The equation applies to the conversion of mass into energy, but the efficiency of such conversion varies greatly depending on the process involved. Nuclear reactions achieve higher efficiencies than chemical reactions.
-
It's not a recipe for limitless energy: While the equation reveals the enormous potential energy stored in matter, harnessing this energy effectively and safely remains a significant technological challenge. Furthermore, the amount of mass that can be converted into energy is limited by the available mass itself.
-
It's not only about nuclear reactions: While prominently featured in nuclear processes, E=mc² applies to all forms of energy and mass transformations, albeit often with smaller and less noticeable mass changes in everyday phenomena.
Conclusion: A Fundamental Equation with Profound Implications
Solving E=mc² for c provides a powerful tool for investigating the relationship between energy and mass. The equation's implications extend far beyond simple calculations, influencing our understanding of nuclear physics, particle physics, astrophysics, and cosmology. It serves as a fundamental pillar of modern physics and continues to inspire scientific exploration and technological advancements. While the simple equation might seem straightforward, its profound implications ripple through the very fabric of our universe, shaping our understanding of reality itself. The ability to solve for 'c' unlocks a deeper understanding of this fundamental constant and its crucial role in the cosmos.
Latest Posts
Latest Posts
-
What Is 10 Of 150 00
Sep 18, 2025
-
60 Degrees Fahrenheit In Celsius
Sep 18, 2025
-
770 070 In Word Form
Sep 18, 2025
-
104 Degree Fahrenheit To Celsius
Sep 18, 2025
-
What Is 5 Of 1000000
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Solve E Mc2 For C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.