Solve The Inequality 8z+3-2z 51
gasmanvison
Sep 25, 2025 · 5 min read
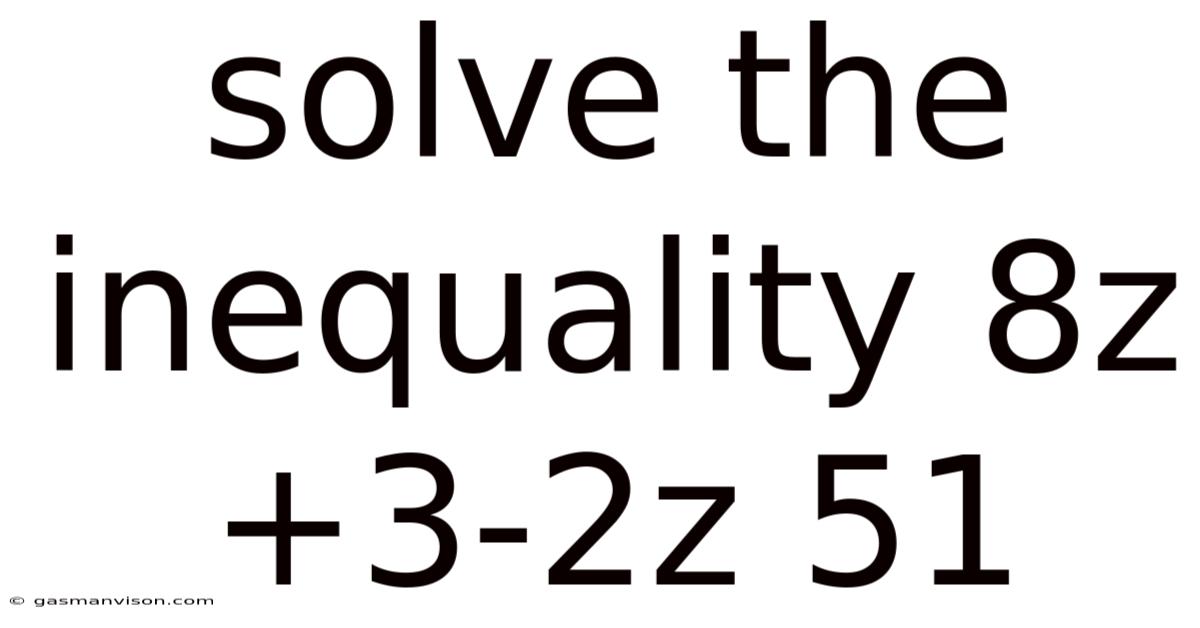
Table of Contents
Solving the Inequality: 8z + 3 - 2z ≤ 51 – A Comprehensive Guide
This article provides a detailed explanation of how to solve the inequality 8z + 3 - 2z ≤ 51, covering not only the solution process but also the underlying principles of inequalities and their applications. We'll explore various aspects, including simplifying expressions, applying inequality properties, representing solutions graphically, and understanding the meaning of the solution set. This guide is designed for students learning algebra and anyone looking to refresh their understanding of solving inequalities.
Meta Description: Learn how to solve the linear inequality 8z + 3 - 2z ≤ 51 step-by-step. This comprehensive guide explains the process, explores related concepts, and shows how to represent the solution graphically. Master inequality solving today!
Understanding Inequalities
Before diving into the solution, let's clarify the fundamental concepts surrounding inequalities. An inequality is a mathematical statement that compares two expressions using inequality symbols:
- ≤ (less than or equal to): The expression on the left is less than or equal to the expression on the right.
- < (less than): The expression on the left is strictly less than the expression on the right.
- ≥ (greater than or equal to): The expression on the left is greater than or equal to the expression on the right.
- > (greater than): The expression on the left is strictly greater than the expression on the right.
Unlike equations, which have a single solution (or a finite number of solutions), inequalities typically have an infinite number of solutions forming a solution set.
Solving the Inequality: 8z + 3 - 2z ≤ 51
Now, let's tackle the inequality 8z + 3 - 2z ≤ 51. The goal is to isolate the variable 'z' on one side of the inequality sign. We achieve this by applying algebraic operations, keeping in mind that certain operations might reverse the inequality sign.
Step 1: Simplify the expression.
First, combine like terms on the left-hand side of the inequality:
8z - 2z + 3 ≤ 51
This simplifies to:
6z + 3 ≤ 51
Step 2: Isolate the term with the variable.
Subtract 3 from both sides of the inequality:
6z + 3 - 3 ≤ 51 - 3
This results in:
6z ≤ 48
Step 3: Solve for the variable.
Divide both sides of the inequality by 6. Since we are dividing by a positive number, the inequality sign remains unchanged:
6z / 6 ≤ 48 / 6
This simplifies to:
z ≤ 8
Therefore, the solution to the inequality 8z + 3 - 2z ≤ 51 is z ≤ 8. This means that any value of z that is less than or equal to 8 will satisfy the original inequality.
Representing the Solution Graphically
The solution z ≤ 8 can be represented graphically on a number line. We would plot a closed circle (or a filled-in dot) at 8, indicating that 8 is included in the solution set, and then shade the region to the left of 8, representing all values less than 8.
[Imagine a number line here with a closed circle at 8 and the region to the left shaded.]
Interval Notation
Another way to represent the solution set is using interval notation. In this case, the solution set is represented as:
(-∞, 8]
The parenthesis '(' indicates that negative infinity is not included in the set (as infinity is not a number), and the square bracket ']' indicates that 8 is included.
Checking the Solution
To verify the solution, we can substitute a value from the solution set (e.g., z = 7) and a value outside the solution set (e.g., z = 9) into the original inequality:
For z = 7:
8(7) + 3 - 2(7) ≤ 51
56 + 3 - 14 ≤ 51
45 ≤ 51 (This is true)
For z = 9:
8(9) + 3 - 2(9) ≤ 51
72 + 3 - 18 ≤ 51
57 ≤ 51 (This is false)
This confirms that our solution, z ≤ 8, is correct.
Applications of Inequalities
Inequalities have a wide range of applications in various fields, including:
-
Physics: Describing ranges of physical quantities like temperature, speed, or pressure. For example, the temperature of a certain chemical reaction must remain below 100°C to avoid undesirable side effects.
-
Engineering: Defining constraints and tolerances in designs. A bridge's weight must be less than a certain limit to ensure its structural integrity.
-
Economics: Modeling economic scenarios, such as profit maximization or cost minimization. A company needs to sell at least 1000 units to break even.
-
Computer Science: Setting bounds for algorithm performance or data structures. An algorithm's execution time should be less than a specified time limit.
Solving More Complex Inequalities
The principles discussed here extend to more complex inequalities. For instance, consider inequalities involving multiple variables, absolute values, or quadratic expressions. These often require more advanced techniques, including factoring, using the quadratic formula, or considering different cases based on the absolute value.
Example: A More Complex Inequality
Let's consider a slightly more challenging inequality: |2x - 1| ≤ 5
Solving this requires considering two cases:
Case 1: 2x - 1 ≥ 0
In this case, the inequality becomes:
2x - 1 ≤ 5
Adding 1 to both sides:
2x ≤ 6
Dividing by 2:
x ≤ 3
Case 2: 2x - 1 < 0
In this case, the inequality becomes:
-(2x - 1) ≤ 5
-2x + 1 ≤ 5
Subtracting 1 from both sides:
-2x ≤ 4
Dividing by -2 (and reversing the inequality sign):
x ≥ -2
Combining both cases, the solution is -2 ≤ x ≤ 3. This can be represented graphically as a closed interval on the number line, shaded between -2 and 3 (inclusive). The interval notation for this is [-2, 3].
Conclusion
Solving inequalities is a crucial skill in algebra and beyond. This comprehensive guide has walked through the steps of solving a linear inequality, explained the underlying principles, and demonstrated how to represent the solution graphically and using interval notation. By understanding these concepts and practicing solving various inequalities, you'll develop a strong foundation for tackling more complex mathematical problems across many different fields. Remember to always check your solutions to ensure they are accurate and consistent with the original inequality. The more you practice, the more confident and proficient you will become in this important area of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve The Inequality 8z+3-2z 51 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.