Solve X 3 2 5
gasmanvison
Sep 15, 2025 · 5 min read
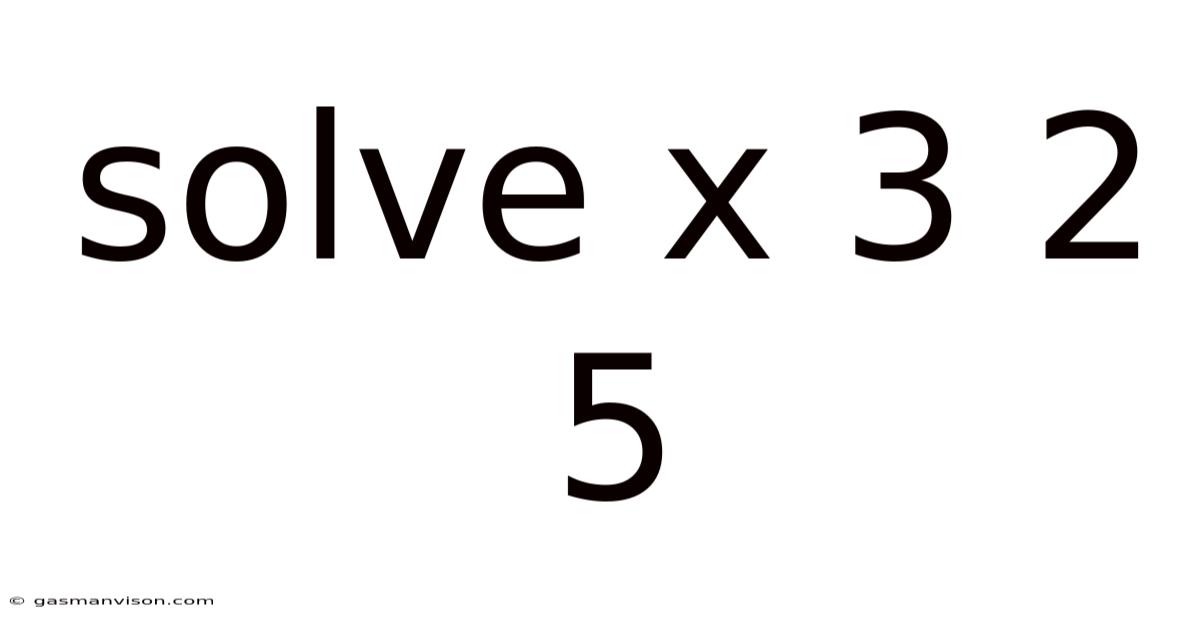
Table of Contents
Solving x³ + 2x = 5: A Deep Dive into Cubic Equation Solutions
This article explores the solution to the cubic equation x³ + 2x = 5, demonstrating various methods for finding real and complex roots. We'll move beyond a simple calculator solution, delving into the underlying mathematical principles and showcasing different approaches to solving cubic equations. Understanding these methods provides a valuable skill set for anyone working with higher-order polynomials in mathematics, engineering, and computer science. This comprehensive guide will equip you with the knowledge to tackle similar cubic equations with confidence.
Understanding Cubic Equations
A cubic equation is a polynomial equation of degree three, meaning the highest power of the variable (x in this case) is 3. The general form is ax³ + bx² + cx + d = 0, where a, b, c, and d are constants, and a ≠ 0. Our specific equation, x³ + 2x = 5, can be rewritten in the standard form:
x³ + 2x - 5 = 0
This seemingly simple equation hides a surprising amount of mathematical depth. Unlike quadratic equations (degree 2), which always have a straightforward solution using the quadratic formula, solving cubic equations often requires more involved techniques.
Method 1: Numerical Methods (Approximation)
When an analytical solution (a precise formula) is difficult or impossible to obtain, numerical methods provide excellent approximations. These iterative methods refine an initial guess until a solution is found to a desired level of accuracy. One common method is the Newton-Raphson method.
The Newton-Raphson method uses the derivative of the function to iteratively improve the approximation. Let f(x) = x³ + 2x - 5. The derivative, f'(x), is 3x² + 2. The iterative formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
Where x_n is the current approximation and x_(n+1) is the improved approximation. Let's start with an initial guess, x_0 = 1:
- Iteration 1: x_1 = 1 - (-2) / 5 = 1.4
- Iteration 2: x_2 = 1.4 - (-0.104) / 7.72 ≈ 1.413
- Iteration 3: x_3 = 1.413 - (-0.0036) / 7.97 ≈ 1.414
Continuing this process, we quickly converge to a solution around x ≈ 1.414. This value is an approximation, and the accuracy depends on the number of iterations and the initial guess. While straightforward to implement computationally, the Newton-Raphson method doesn't provide an exact solution; it's an iterative approach.
Method 2: Graphical Method
A graphical approach provides a visual representation of the solution. By plotting the function y = x³ + 2x - 5, the x-intercept(s) represent the root(s) of the equation. The x-intercept is where y = 0, which is the solution to our cubic equation.
Plotting this function, we observe that it intersects the x-axis at approximately x ≈ 1.414. This confirms the result obtained through the Newton-Raphson method. The graphical method is intuitive and visually appealing, providing a quick estimate of the solution's value. However, it's not as precise as numerical methods or an analytical solution, and relies on the accuracy of the graph.
Method 3: Cardano's Method (Analytical Solution)
Cardano's method provides an analytical solution for cubic equations. However, it involves complex numbers even when the final solution is a real number. The general formula is complex and computationally intensive, making numerical methods preferable for many practical applications. Let's briefly outline the steps:
-
Depressed Cubic: Transform the equation into a depressed cubic form, eliminating the x² term. This is done by substituting x = y - (b/3a) in the general cubic equation ax³ + bx² + cx + d = 0. In our case, b = 0, so the equation remains unchanged.
-
Cardano's Formula: The depressed cubic y³ + py + q = 0 is solved using the following formula:
y = ∛((-q/2) + √((q²/4) + (p³/27))) + ∛((-q/2) - √((q²/4) + (p³/27)))
Where p = 2 and q = -5 for our equation.
- Calculation and Simplification: Substituting the values of p and q into Cardano's formula involves complex calculations and potentially dealing with complex cube roots. The result, after careful simplification, will yield the real root we've already approximated.
While Cardano's method gives an exact analytical solution, it is significantly more complex than numerical methods and can be cumbersome to apply manually.
Method 4: Using a Calculator or Software
Most scientific calculators and mathematical software packages (like Mathematica, Maple, or even online calculators) have built-in functions to solve polynomial equations. Simply input the coefficients (1, 0, 2, -5) and the software will provide the roots, including both real and complex solutions. This is the easiest approach for obtaining a solution, but it does not provide an understanding of the underlying mathematical principles.
Exploring the Real Root and Complex Roots
Our equation x³ + 2x - 5 = 0 has one real root, approximately 1.414. Cubic equations can have up to three roots (including complex roots). While numerical methods like Newton-Raphson efficiently find the real root, determining complex roots might require more advanced techniques like the cubic formula or software tools. The real root, as we’ve discovered through several methods, is approximately 1.414. This is often represented with greater precision as a root that is close to the irrational number √2 ≈ 1.41421356... This highlights the possibility of irrational roots within cubic equations.
Significance and Applications
Solving cubic equations has wide-ranging applications in various fields:
- Engineering: Designing structures, analyzing circuits, and solving problems in fluid dynamics often involve cubic equations.
- Physics: Modeling physical phenomena, such as projectile motion or oscillations, might require solving cubic equations.
- Computer Graphics: Cubic curves (Bézier curves, for instance) are fundamental in computer-aided design and graphics. Solving equations related to these curves involves cubic equation solutions.
- Economics: Certain economic models utilize cubic equations to represent relationships between variables.
Conclusion
Solving x³ + 2x = 5 involves understanding the nuances of cubic equations. We've explored several methods, from iterative numerical approaches (like Newton-Raphson) to the more complex analytical solution offered by Cardano's method. The ease of use and speed of numerical methods often make them preferable for practical applications, while Cardano's method offers the theoretical satisfaction of an exact solution. Regardless of the chosen method, understanding the process of solving cubic equations is a valuable asset in various mathematical and scientific endeavors. The approximately solution of x ≈ 1.414 serves as a critical result showcasing the culmination of different mathematical techniques applied to a single problem. Remember that exploration and understanding of these different methods offer a comprehensive understanding of the solution beyond a simple numerical answer.
Latest Posts
Latest Posts
-
Does Erosion Make A Sound
Sep 15, 2025
-
Who Was The Heaviest President
Sep 15, 2025
-
First 30 Digits Of Pi
Sep 15, 2025
-
Because There Were Extenuating Circumstances
Sep 15, 2025
-
How Much Is 3000 Pennies
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Solve X 3 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.