Square Root Of 28 Simplified
gasmanvison
Sep 17, 2025 · 5 min read
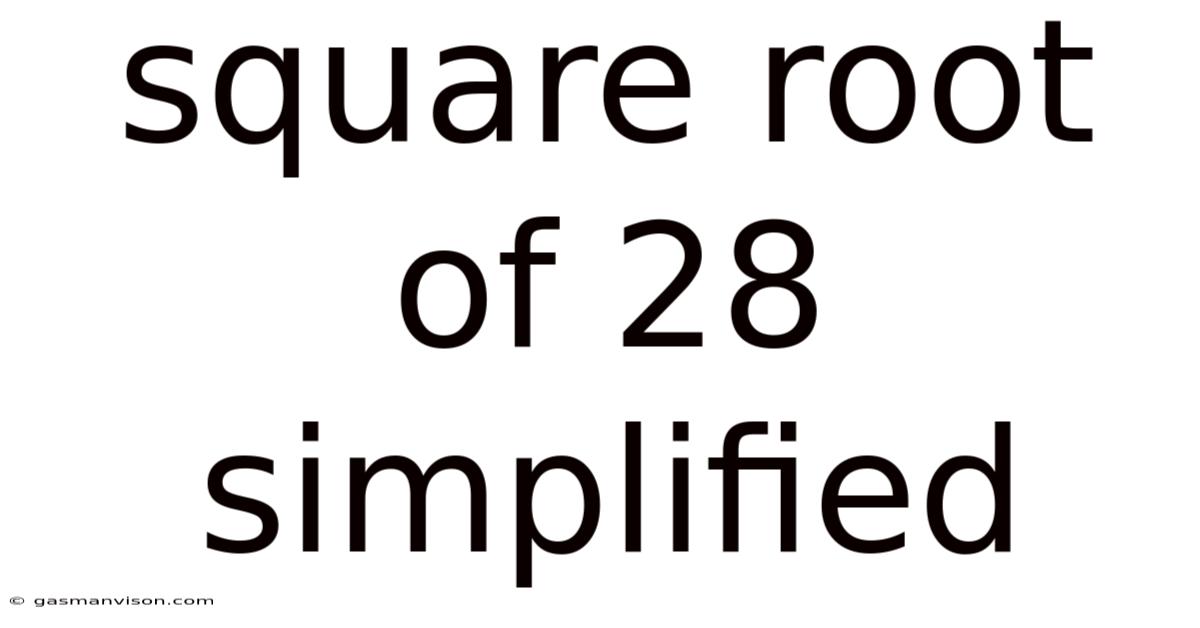
Table of Contents
Unveiling the Mystery: Simplifying the Square Root of 28
The square root of 28, denoted as √28, might seem like a straightforward mathematical concept, but delving deeper reveals a fascinating journey into prime factorization, radical simplification, and the fundamental principles of number theory. This article will not only show you how to simplify √28 but will also explore the underlying concepts, providing you with a comprehensive understanding of this seemingly simple square root. This exploration will equip you with the skills to simplify other square roots and solidify your understanding of mathematical principles.
What is a Square Root?
Before we dive into simplifying √28, let's establish a clear understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 multiplied by 3 equals 9. The square root operation is the inverse of squaring a number.
Simplifying √28: A Step-by-Step Approach
The key to simplifying square roots like √28 lies in the concept of prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Here's how to simplify √28 using prime factorization:
-
Find the prime factorization of 28: We start by finding the prime factors of 28. We can do this through a factor tree or by repeatedly dividing by prime numbers.
28 = 2 x 14 14 = 2 x 7
Therefore, the prime factorization of 28 is 2 x 2 x 7, or 2² x 7.
-
Rewrite the square root using prime factors: Now, we can rewrite √28 using the prime factorization we just found:
√28 = √(2² x 7)
-
Apply the square root property: The square root of a product is equal to the product of the square roots. This allows us to separate the terms:
√(2² x 7) = √2² x √7
-
Simplify the perfect square: The square root of 2² is simply 2 (because 2 x 2 = 4, and √4 = 2). Therefore:
√2² x √7 = 2√7
Therefore, the simplified form of √28 is 2√7. This means that 2√7, when squared, will equal 28.
Understanding the Concept of Radicals and Simplification
The expression 2√7 is a radical expression. A radical expression is an expression containing a radical symbol (√), indicating a root (in this case, a square root). Simplifying a radical expression involves reducing it to its simplest form, removing any perfect square factors from under the radical. This simplification process makes the radical expression easier to work with and understand.
Why Simplify Radicals?
Simplifying radicals isn't just about aesthetics; it's about mathematical precision and efficiency. Simplified radicals provide a more concise and manageable representation of the number. Furthermore, simplified radicals are essential for solving equations, simplifying expressions, and performing calculations involving square roots. They also facilitate easier comparisons between different radical expressions.
Further Exploration: Simplifying Other Square Roots
The process we used to simplify √28 can be applied to simplify other square roots. Let's explore a few more examples:
-
√48:
- Prime factorization: 48 = 2 x 2 x 2 x 2 x 3 = 2⁴ x 3
- Rewriting with prime factors: √48 = √(2⁴ x 3)
- Applying the square root property: √(2⁴ x 3) = √2⁴ x √3
- Simplifying the perfect square: √2⁴ = 2² = 4
- Simplified form: 4√3
-
√75:
- Prime factorization: 75 = 3 x 5 x 5 = 3 x 5²
- Rewriting with prime factors: √75 = √(3 x 5²)
- Applying the square root property: √(3 x 5²) = √3 x √5²
- Simplifying the perfect square: √5² = 5
- Simplified form: 5√3
-
√12:
- Prime factorization: 12 = 2 x 2 x 3 = 2² x 3
- Rewriting with prime factors: √12 = √(2² x 3)
- Applying the square root property: √(2² x 3) = √2² x √3
- Simplifying the perfect square: √2² = 2
- Simplified form: 2√3
Advanced Concepts: Beyond Simplification
While simplifying radicals is a fundamental skill, the world of square roots extends beyond this. Here are a few advanced concepts to consider:
-
Estimating Square Roots: When dealing with square roots of non-perfect squares (like √28), you can use estimation techniques to approximate their values. For example, you know that √25 = 5 and √36 = 6, so √28 must be somewhere between 5 and 6.
-
Operations with Radicals: You can perform addition, subtraction, multiplication, and division with radical expressions, but certain rules and simplification strategies apply.
-
Rationalizing the Denominator: When a radical expression has a radical in the denominator, you often need to rationalize the denominator – that is, eliminate the radical from the denominator by multiplying the numerator and denominator by a suitable expression.
Real-World Applications:
Square roots and their simplification aren't just abstract mathematical concepts; they have numerous applications in various fields:
-
Geometry: Calculating the diagonal of a square or the hypotenuse of a right-angled triangle often involves square roots.
-
Physics: Many physics formulas, especially those related to motion, energy, and waves, incorporate square roots.
-
Engineering: Structural engineers use square roots in calculations related to stress, strain, and stability.
-
Computer Graphics: Square roots are used extensively in computer graphics and game development for calculations related to 3D transformations and animations.
Conclusion:
Simplifying the square root of 28, or any square root, involves understanding the process of prime factorization and applying the fundamental properties of square roots. Mastering this skill is crucial for building a strong foundation in algebra and various other mathematical disciplines. The ability to simplify radicals isn't merely a procedural skill; it's a gateway to a deeper understanding of number theory and its applications in the real world. By continuing to explore these concepts and practicing regularly, you can build confidence and competence in handling more complex mathematical problems. The seemingly simple act of simplifying √28 opens doors to a much broader and fascinating mathematical landscape.
Latest Posts
Latest Posts
-
Utang Na Loob In English
Sep 17, 2025
-
For Which Value Of Is
Sep 17, 2025
-
How Far Is 5000 Meters
Sep 17, 2025
-
Commercial Zones Require Vigilance Because
Sep 17, 2025
-
Convert 170 Pounds To Kilograms
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 28 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.