Square Root Of 32 Simplified
gasmanvison
Sep 08, 2025 · 5 min read
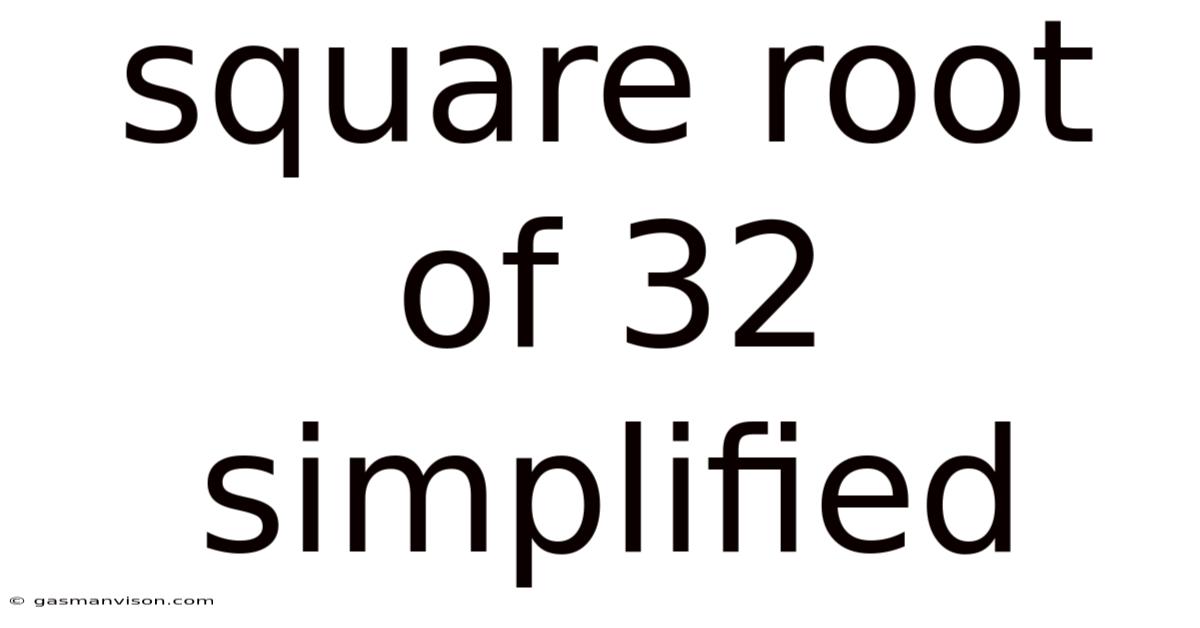
Table of Contents
Simplifying the Square Root of 32: A Comprehensive Guide
Finding the square root of 32 might seem like a simple task at first glance, but understanding how to simplify it reveals a deeper understanding of mathematical principles. This comprehensive guide will explore various methods for simplifying √32, delve into the underlying concepts of radicals and prime factorization, and equip you with the tools to tackle similar problems with ease. This article will cover everything from basic simplification techniques to advanced strategies, ensuring a thorough grasp of this fundamental mathematical concept.
What is a Square Root?
Before we dive into simplifying √32, let's establish a clear understanding of what a square root represents. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Square roots are crucial in various mathematical fields, from geometry (calculating areas and volumes) to algebra (solving equations). Understanding square roots is fundamental for more advanced mathematical concepts.
Prime Factorization: The Key to Simplification
The most efficient method for simplifying square roots involves prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This process is the cornerstone of simplifying radicals, allowing us to identify perfect square factors within the number.
Let's apply this to 32:
-
Find the prime factors: 32 can be broken down as follows: 32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
-
Identify perfect squares: Notice that we have five factors of 2. We can rewrite this as (2<sup>2</sup>) x (2<sup>2</sup>) x 2. 2<sup>2</sup> is a perfect square (4 x 4 = 16).
-
Simplify the square root: Now we can rewrite √32 as √[(2<sup>2</sup>) x (2<sup>2</sup>) x 2]. Since √(a x b) = √a x √b, we can separate this into: √(2<sup>2</sup>) x √(2<sup>2</sup>) x √2. This simplifies to 2 x 2 x √2 = 4√2.
Therefore, the simplified form of √32 is 4√2.
Alternative Methods for Simplification
While prime factorization is the most systematic approach, other methods can help visualize the simplification process. Let's explore some alternatives:
-
Recognizing Perfect Square Factors: This involves identifying perfect squares that are factors of the number under the square root. For 32, we might recognize that 16 is a perfect square (4 x 4 = 16) and a factor of 32 (16 x 2 = 32). This allows us to rewrite √32 as √(16 x 2) = √16 x √2 = 4√2. This method relies on familiarity with perfect squares.
-
Repeated Division: This iterative method involves repeatedly dividing the number by perfect squares until you are left with a number that does not contain any perfect square factors. For 32:
- Divide by 4: 32 / 4 = 8
- Divide by 4 again: 8 / 4 = 2
This leaves us with 4 x 4 x 2. Taking the square root gives us 4√2. This method can be less efficient for larger numbers.
Understanding Radicals and their Properties
Simplifying square roots involves a firm grasp of radical properties. These properties govern how we manipulate expressions containing radicals. Key properties include:
- √(a x b) = √a x √b: The square root of a product is the product of the square roots.
- √(a / b) = √a / √b: The square root of a quotient is the quotient of the square roots.
- (√a)<sup>2</sup> = a: Squaring a square root results in the original number.
- √a x √a = a: Multiplying a square root by itself results in the original number.
Understanding these properties is crucial for manipulating and simplifying more complex radical expressions.
Advanced Examples and Applications
Let's expand our understanding by tackling more complex examples:
Example 1: Simplifying √72
-
Prime Factorization: 72 = 2 x 36 = 2 x 6 x 6 = 2 x 2 x 3 x 2 x 3 = 2<sup>3</sup> x 3<sup>2</sup>
-
Identifying Perfect Squares: We have 2<sup>2</sup> and 3<sup>2</sup>.
-
Simplification: √72 = √(2<sup>2</sup> x 3<sup>2</sup> x 2) = √(2<sup>2</sup>) x √(3<sup>2</sup>) x √2 = 2 x 3 x √2 = 6√2
Therefore, √72 simplifies to 6√2.
Example 2: Simplifying √108
-
Prime Factorization: 108 = 2 x 54 = 2 x 2 x 27 = 2 x 2 x 3 x 9 = 2 x 2 x 3 x 3 x 3 = 2<sup>2</sup> x 3<sup>3</sup>
-
Identifying Perfect Squares: We have 2<sup>2</sup> and 3<sup>2</sup>.
-
Simplification: √108 = √(2<sup>2</sup> x 3<sup>2</sup> x 3) = √(2<sup>2</sup>) x √(3<sup>2</sup>) x √3 = 2 x 3 x √3 = 6√3
Therefore, √108 simplifies to 6√3.
Applications in Geometry and Other Fields
Simplifying square roots isn't just a theoretical exercise. It has practical applications in various fields, particularly geometry:
-
Calculating the Diagonal of a Square: The diagonal of a square with side length 's' is given by s√2. Simplifying this expression is crucial for precise calculations.
-
Calculating the Hypotenuse of a Right-Angled Triangle: The Pythagorean theorem (a² + b² = c²) frequently involves square roots when calculating the length of the hypotenuse. Simplifying these square roots leads to more concise and understandable results.
-
Area and Volume Calculations: Many area and volume formulas involve square roots. Simplifying these square roots makes calculations more efficient and accurate.
Conclusion: Mastering Square Root Simplification
Mastering the simplification of square roots, such as √32, is fundamental to success in mathematics and related fields. Through prime factorization, understanding radical properties, and practicing various simplification techniques, you can confidently tackle more complex radical expressions. This skillset extends beyond simple calculations and provides a solid foundation for advanced mathematical concepts and applications in diverse fields like geometry, physics, and engineering. Remember to always look for perfect square factors within the number to achieve the most simplified form. Practice consistently, and you’ll soon find simplifying square roots becomes second nature.
Latest Posts
Latest Posts
-
To Generate An Idea Means
Sep 08, 2025
-
The Term Mdf Refers To
Sep 08, 2025
-
Is Width Same As Depth
Sep 08, 2025
-
The Distance Between Two Pitches
Sep 08, 2025
-
Florida Hiv Aids Final Evaluation
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 32 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.