Square Root Of 98 Simplified
gasmanvison
Sep 24, 2025 · 5 min read
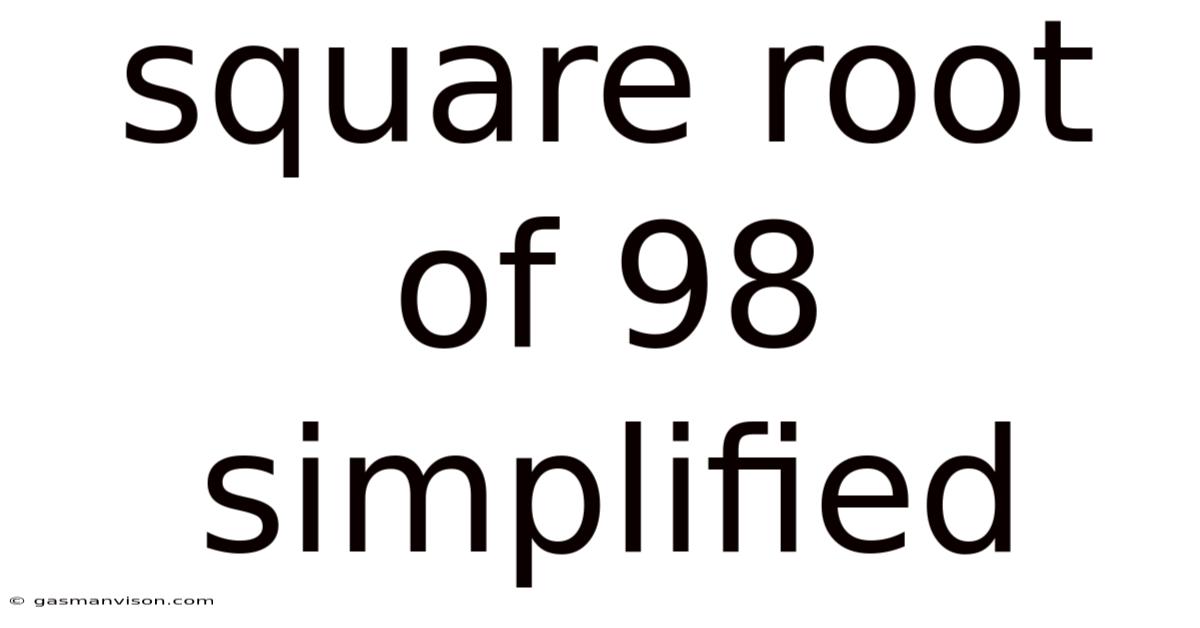
Table of Contents
Simplifying the Square Root of 98: A Comprehensive Guide
Finding the square root of 98 might seem straightforward at first glance, but simplifying the answer to its most reduced form involves understanding prime factorization and simplifying radicals. This article will delve deep into the process, exploring various methods and providing a solid foundation for simplifying other square roots. We'll cover everything from the basics of square roots and prime factorization to advanced techniques and real-world applications. This guide aims to equip you with the knowledge to confidently tackle similar problems.
What is a Square Root?
Before diving into the simplification of √98, let's revisit the fundamental concept of a square root. A square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 25 (√25) is 5 because 5 x 5 = 25. However, many numbers don't have whole number square roots. This is where simplification comes into play.
Prime Factorization: The Key to Simplification
Prime factorization is the cornerstone of simplifying square roots. It involves breaking down a number into its prime factors—numbers divisible only by 1 and themselves. To simplify √98, we first need to find its prime factorization.
-
Start with the smallest prime number: We begin by dividing 98 by the smallest prime number, 2. 98 ÷ 2 = 49.
-
Continue the process: Now we have 2 x 49. 49 is not divisible by 2, so we move to the next prime number, 7. 49 ÷ 7 = 7.
-
Identify the prime factors: We've now broken down 98 into its prime factors: 2 x 7 x 7. This can also be written as 2 x 7².
Simplifying the Square Root
Now that we have the prime factorization of 98 (2 x 7²), we can simplify the square root. Remember that the square root of a product is the product of the square roots. This allows us to rewrite √98 as follows:
√98 = √(2 x 7²) = √2 x √7²
Since √7² = 7 (because 7 x 7 = 49), we can simplify further:
√98 = 7√2
Therefore, the simplified form of √98 is 7√2. This is the most reduced form because 2 is a prime number and cannot be further simplified within the square root.
Alternative Methods for Simplification
While the prime factorization method is the most common and generally preferred, there are other approaches to simplifying square roots, although they often rely on recognizing perfect squares within the number.
Method 1: Identifying Perfect Square Factors
This method involves recognizing perfect squares that are factors of the number under the square root. A perfect square is a number that is the square of an integer (e.g., 4, 9, 16, 25, etc.).
Looking at 98, we can identify that 49 (7²) is a factor of 98 (98 = 49 x 2). Therefore:
√98 = √(49 x 2) = √49 x √2 = 7√2
This method is faster if you readily recognize perfect square factors. However, it might be less reliable for larger numbers where identifying factors is challenging.
Method 2: Repeated Division by Prime Numbers
This is a more systematic version of prime factorization, especially helpful when dealing with larger numbers. It involves repeatedly dividing the number by the smallest prime number until you reach 1. Let's illustrate with 98:
- 98 ÷ 2 = 49
- 49 ÷ 7 = 7
- 7 ÷ 7 = 1
This reveals the prime factorization 2 x 7 x 7, leading to the same simplified form: 7√2.
Understanding Radical Expressions
The simplified form 7√2 is a radical expression. Understanding these expressions is crucial for further manipulation and simplification of square roots. A radical expression consists of a radicand (the number inside the radical symbol) and a radical (the symbol itself, √). In 7√2, 2 is the radicand, and the entire expression is a radical expression.
Operations with Radical Expressions
Once you understand how to simplify radical expressions, you can perform various operations on them, such as addition, subtraction, multiplication, and division. However, these operations require like radicals (radicals with the same radicand). For example, you can add 3√2 and 5√2 because they have the same radicand (2): 3√2 + 5√2 = 8√2. However, adding 3√2 and 5√3 requires additional steps, often involving simplification before addition is possible.
Applications of Simplifying Square Roots
Simplifying square roots isn't just an academic exercise; it has practical applications in various fields:
- Geometry: Calculating distances, areas, and volumes often involve square roots. Simplifying the results makes them easier to interpret and use.
- Physics: Many physics formulas involve square roots, particularly in areas like mechanics and electromagnetism. Simplification is crucial for accurate and efficient calculations.
- Engineering: Similar to physics, engineering problems frequently require simplifying square roots for precise calculations and design.
- Computer Graphics: Square roots play a significant role in 3D graphics and game development for calculating distances and vectors. Efficient simplification is important for optimal performance.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, exploring more advanced concepts related to square roots and radicals can be highly beneficial. These concepts include:
- Rationalizing the Denominator: This technique eliminates radicals from the denominator of a fraction involving radicals.
- Solving Quadratic Equations: Quadratic equations often involve square roots in their solutions.
- Complex Numbers: The square root of a negative number introduces the concept of imaginary and complex numbers.
Conclusion:
Simplifying the square root of 98, resulting in 7√2, involves understanding prime factorization and manipulating radical expressions. Mastering this process opens doors to a deeper understanding of algebra and its practical applications in numerous fields. By applying the methods described above and consistently practicing, you'll build confidence and proficiency in simplifying square roots and tackling more complex mathematical problems. Remember that consistent practice and a thorough understanding of the underlying principles are key to mastering this important mathematical skill. Don't hesitate to explore further resources and tackle more challenging examples to solidify your understanding.
Latest Posts
Latest Posts
-
Average Iq Of Black Americans
Sep 24, 2025
-
What Is 4 Times 8
Sep 24, 2025
-
Whats The Capital Of Pennsylvania
Sep 24, 2025
-
Whats Another Word For Factor
Sep 24, 2025
-
What Are Some Structural Features
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 98 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.