The Diagram Represents 6x2-7x 2
gasmanvison
Sep 06, 2025 · 5 min read
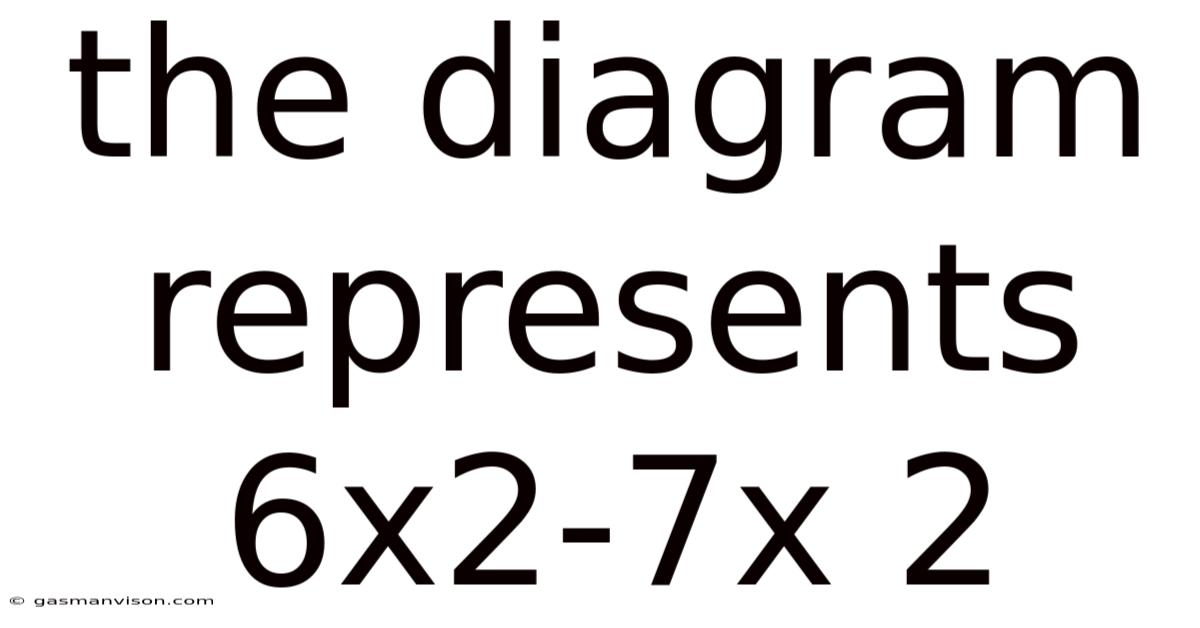
Table of Contents
Deconstructing the Diagram: A Deep Dive into 6x² - 7x + 2
This article will explore the multifaceted representation of the quadratic expression 6x² - 7x + 2. We'll move beyond a simple algebraic understanding to examine its graphical representation, factoring methods, and the practical applications of such expressions in various fields. Understanding this seemingly simple equation opens doors to a deeper appreciation of algebra and its real-world implications.
Understanding the Quadratic Expression
The expression 6x² - 7x + 2 is a quadratic equation, characterized by its highest power of x being 2. This type of equation, when graphed, produces a parabola – a symmetrical U-shaped curve. The coefficients (6, -7, and 2) determine the shape, orientation, and position of this parabola on a Cartesian plane. The term 6x² is the quadratic term, -7x is the linear term, and 2 is the constant term. These terms contribute uniquely to the overall behavior of the equation.
Graphical Representation: The Parabola
Plotting the quadratic equation 6x² - 7x + 2 on a graph reveals a parabola that opens upwards (since the coefficient of x² is positive). The parabola's vertex represents the minimum value of the function. The x-intercepts (where the parabola intersects the x-axis) represent the roots or solutions to the equation 6x² - 7x + 2 = 0. These roots are crucial for understanding the behavior of the function and are directly related to the factored form of the quadratic expression. The y-intercept (where the parabola intersects the y-axis) is simply the constant term, in this case, 2.
Analyzing the graph provides valuable insights. For instance, we can visually determine the range of x values for which the function is positive or negative. The axis of symmetry, a vertical line passing through the vertex, divides the parabola into two mirror images. This symmetry is a fundamental characteristic of all parabolas representing quadratic functions.
Factoring the Quadratic Expression: Unveiling the Roots
Finding the roots of the quadratic equation is equivalent to factoring the expression 6x² - 7x + 2. Several methods can achieve this, including:
-
Trial and Error: This method involves finding two binomials whose product equals the original quadratic expression. We look for factors of 6 (coefficients of x²) and 2 (the constant term) that, when combined according to the FOIL method (First, Outer, Inner, Last), yield the middle term (-7x). In this case, the factors are (2x - 1) and (3x - 2). Thus, 6x² - 7x + 2 = (2x - 1)(3x - 2).
-
Quadratic Formula: For more complex quadratic equations where factoring by trial and error is difficult, the quadratic formula provides a reliable solution. The formula is: x = [-b ± √(b² - 4ac)] / 2a, where a, b, and c are the coefficients of the quadratic equation ax² + bx + c. In our case, a = 6, b = -7, and c = 2. Applying the formula will yield the same roots as the factoring method.
-
Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. While effective, it is often more complex than trial and error or the quadratic formula for simpler quadratic equations.
The Significance of the Roots
The roots of the quadratic equation, obtained through factoring or the quadratic formula, represent the x-values where the parabola intersects the x-axis. These points are crucial for understanding several aspects of the function:
-
Solving Equations: If the equation 6x² - 7x + 2 = 0 represents a real-world problem (such as calculating the trajectory of a projectile), the roots represent the points where the solution is zero.
-
Analyzing the Function's Behavior: The roots define the intervals where the function is positive or negative. For x values between the roots, the function is negative; outside the roots, it's positive.
-
Finding the Vertex: The x-coordinate of the parabola's vertex is the average of the roots. This is a useful property for quickly locating the minimum point of the parabola.
Applications of Quadratic Equations
Quadratic equations, like 6x² - 7x + 2, have widespread applications in various fields:
-
Physics: Calculating projectile motion, determining the path of a thrown object, and analyzing the relationship between time, velocity, and distance.
-
Engineering: Designing parabolic antennas, bridges, and arches; optimizing structural designs.
-
Economics: Modeling cost, revenue, and profit functions; analyzing supply and demand.
-
Computer Graphics: Creating curves and shapes in computer-aided design (CAD) software; generating realistic simulations.
-
Data Analysis: Fitting curves to data points; using quadratic regression to predict future trends.
In each of these fields, understanding how to solve and interpret quadratic equations is vital for accurate modeling and prediction.
Beyond the Basics: Exploring Further Concepts
The exploration of 6x² - 7x + 2 extends beyond the basic concepts of factoring and graphing. Further investigation can include:
-
Discriminant: The discriminant (b² - 4ac) within the quadratic formula determines the nature of the roots. If positive, there are two distinct real roots; if zero, there's one repeated real root; if negative, there are two complex roots.
-
Vertex Form: The quadratic equation can be rewritten in vertex form, y = a(x - h)² + k, where (h, k) represents the coordinates of the vertex. This form simplifies calculations and provides a clearer understanding of the parabola's properties.
-
Calculus Applications: Derivatives and integrals can be used to analyze the slope of the parabola at any point and calculate the area under the curve.
-
Matrices and Linear Algebra: Quadratic equations can be represented and solved using matrix methods, providing alternative approaches to problem-solving.
Conclusion: The Power of a Simple Equation
The seemingly simple quadratic expression 6x² - 7x + 2 unveils a rich tapestry of mathematical concepts and practical applications. From understanding its graphical representation as a parabola to factoring it to find its roots, each step contributes to a broader understanding of algebra and its real-world significance. By mastering these techniques, we gain the tools to solve complex problems across numerous scientific and engineering disciplines, highlighting the power and versatility of even seemingly basic algebraic equations. The journey from a simple equation to a deep understanding of its intricacies demonstrates the beauty and power of mathematical exploration. The more we delve into these fundamentals, the more prepared we are to tackle more advanced mathematical concepts and apply them to real-world challenges.
Latest Posts
Latest Posts
-
Lewis Dot Structure For Ch3coch3
Sep 06, 2025
-
By Stimulating Secretion Of Peptidases
Sep 06, 2025
-
Rural Vs Suburban Vs Urban
Sep 06, 2025
-
Your Base Salary Is 20000
Sep 06, 2025
-
Stub Connections Are Used
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about The Diagram Represents 6x2-7x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.