What Is 1/2 Of 1/3
gasmanvison
Sep 22, 2025 · 5 min read
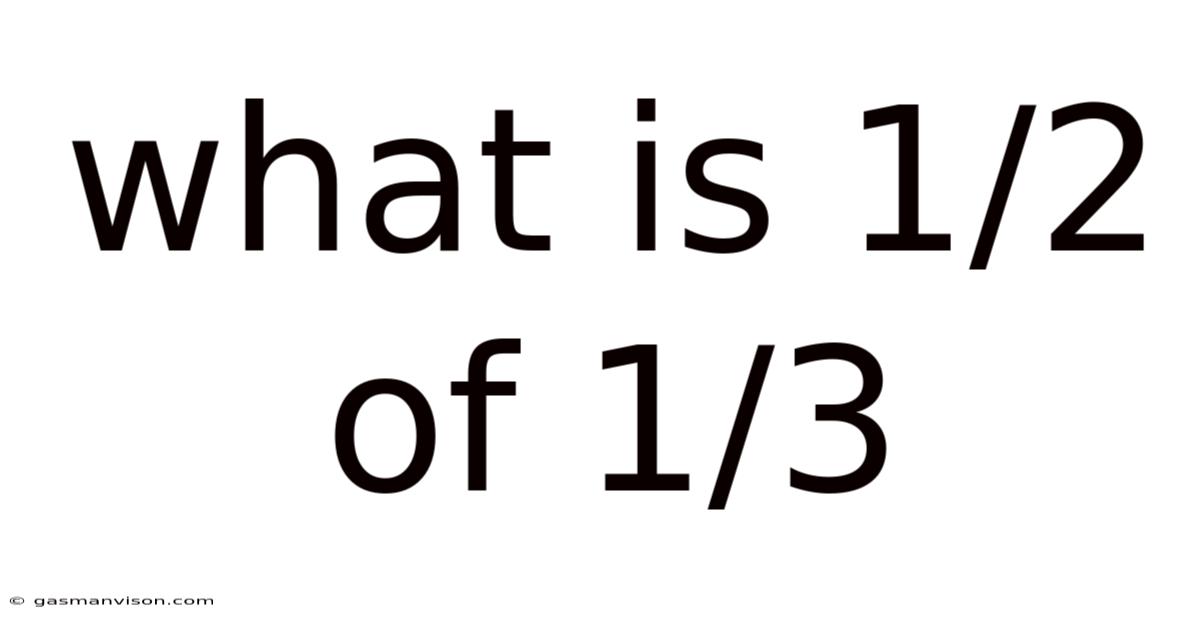
Table of Contents
What is 1/2 of 1/3? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is 1/2 of 1/3?", opens a door to a broader understanding of fractions, their manipulation, and their real-world applications. While the answer itself is straightforward, exploring the process unveils fundamental mathematical concepts crucial for various fields. This article will not only solve the problem but also delve into the underlying principles, providing examples and practical uses of fractional calculations.
Understanding Fractions: Building Blocks of Mathematics
Before tackling the problem, let's establish a solid foundation in understanding fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For instance, 1/3 represents one part out of three equal parts.
Methods for Calculating 1/2 of 1/3
There are two primary methods for calculating half of one-third:
1. Multiplication: The phrase "of" in mathematics often implies multiplication. Therefore, finding 1/2 of 1/3 is equivalent to multiplying 1/2 by 1/3.
To multiply fractions, we multiply the numerators together and the denominators together:
(1/2) * (1/3) = (1 * 1) / (2 * 3) = 1/6
Therefore, 1/2 of 1/3 is 1/6.
2. Visual Representation: A visual approach can enhance understanding, particularly for those who prefer a more intuitive method. Imagine a rectangular shape representing a whole.
- Divide into thirds: Divide the rectangle into three equal parts. Each part represents 1/3.
- Half of one-third: Now, take one of these thirds and divide it in half. This smaller section represents 1/2 of 1/3.
- The whole picture: Observe that the whole rectangle is now divided into six equal parts, and the smaller section represents one of those six parts, confirming that 1/2 of 1/3 is 1/6.
Expanding on Fractions: Practical Applications and Advanced Concepts
The simple calculation of 1/2 of 1/3 serves as a gateway to more complex fractional operations and their relevance in various fields:
1. Cooking and Baking: Recipes often involve fractions. Understanding fractional calculations is essential for adjusting recipes, scaling them up or down, and ensuring accurate measurements. For example, if a recipe calls for 1/3 cup of sugar, and you only want to make half the recipe, you'll need to calculate 1/2 of 1/3 cup, which is 1/6 cup.
2. Construction and Engineering: Precision is paramount in construction and engineering. Fractions are used extensively in blueprints, measurements, and material calculations. Engineers use fractions to calculate load-bearing capacities, dimensions, and material quantities. Imagine calculating the area of a triangular section of a building – fractional calculations are indispensable.
3. Finance and Economics: Fractions are fundamental in financial calculations, including interest rates, stock prices, and investment returns. Understanding fractions helps in calculating portions of investments, interest accrued, or profit margins. For example, calculating a 1/3 profit share from a 1/2 investment requires fractional calculations.
4. Data Analysis and Statistics: Fractions play a crucial role in data analysis and statistics. Representing proportions, percentages, and probabilities often involves fractional values. In data visualization, fractions contribute to understanding proportions within charts and graphs. For instance, analyzing survey results that show 1/3 respondents prefer option A, and calculating 1/2 of that group might involve fractional operations.
5. Science and Medicine: Scientific measurements and experiments often involve fractions. Precise measurements, dilutions, and calculations in chemistry, physics, and biology rely on a solid grasp of fractions. For instance, in a laboratory setting, diluting a solution to 1/3 of its original concentration, and then further diluting to 1/2 of the diluted solution necessitates accurate fractional calculation.
Beyond the Basics: Working with More Complex Fractions
While 1/2 of 1/3 provides a basic example, fractional calculations can become more complex. Let's explore some scenarios:
-
Mixed Numbers: Mixed numbers combine a whole number and a fraction (e.g., 1 1/2). To multiply mixed numbers, convert them into improper fractions first (e.g., 1 1/2 becomes 3/2).
-
Adding and Subtracting Fractions: Adding and subtracting fractions require a common denominator. Find the least common multiple (LCM) of the denominators to achieve this.
-
Dividing Fractions: Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
-
Fractions and Decimals: Converting between fractions and decimals is crucial for various calculations. Remember that a fraction is simply a division problem.
Mastering Fractions: A Continuous Learning Process
The ability to work confidently with fractions is a cornerstone of mathematical literacy. While the calculation of 1/2 of 1/3 may seem elementary, understanding the underlying principles and applying these concepts to more complex scenarios is essential for academic success and professional competence.
Conclusion: The Significance of Fractional Understanding
This article has demonstrated that the seemingly simple question "What is 1/2 of 1/3?" opens the door to a wealth of mathematical concepts and real-world applications. By mastering the fundamentals of fractions, from basic multiplication to more complex operations, individuals equip themselves with a valuable skill applicable across numerous disciplines. This knowledge is not only crucial for academic success but also provides a solid foundation for navigating everyday situations requiring precise calculations and proportional reasoning. Remember, consistent practice and exploration of diverse applications are key to building fluency and confidence in working with fractions.
Latest Posts
Latest Posts
-
2 5 Liters How Many Cups
Sep 22, 2025
-
How Much Is 12 Teaspoons
Sep 22, 2025
-
Rio Bravo Del Norte River
Sep 22, 2025
-
4 1 Independent Practice Answer Key
Sep 22, 2025
-
Continuous Body House Or Senate
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.