What Is 10 Of 80000
gasmanvison
Sep 19, 2025 · 5 min read
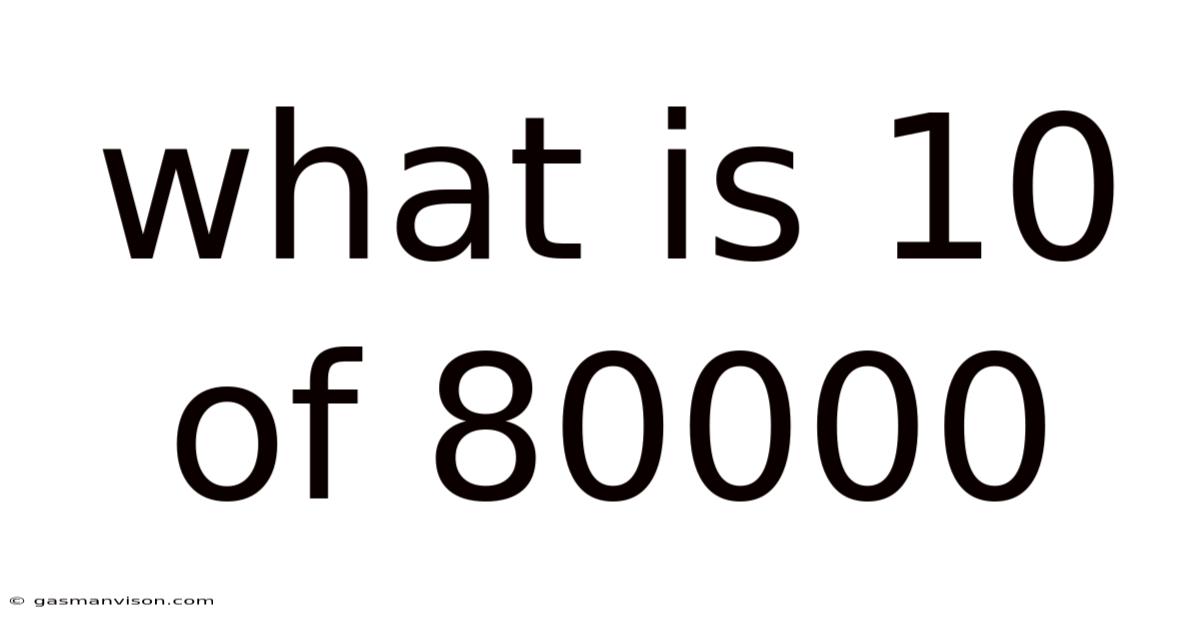
Table of Contents
What is 10/80000? Understanding Percentages and Proportions
This seemingly simple question, "What is 10/80000?", delves into the fundamental concepts of fractions, percentages, and proportions. While a calculator can quickly provide the numerical answer, understanding the underlying principles offers a deeper grasp of mathematical relationships and their applications in various fields. This article will not only provide the answer but also explore the broader context of this calculation, demonstrating its practical relevance and exploring related mathematical concepts.
Meta Description: Learn how to calculate 10/80000 and understand the underlying principles of fractions, percentages, and proportions. This comprehensive guide explores the practical applications of this calculation and provides further insights into related mathematical concepts.
Calculating 10/80000: The Basic Approach
The most straightforward approach is to treat 10/80000 as a simple fraction. We can express this as a decimal by dividing 10 by 80000:
10 ÷ 80000 = 0.000125
This decimal represents the proportion of 10 out of 80000. To express this as a percentage, we multiply the decimal by 100:
0.000125 × 100 = 0.0125%
Therefore, 10 out of 80000 is 0.0125%. This signifies that 10 represents a very small fraction of the total 80000.
Understanding Fractions and Their Components
A fraction, like 10/80000, consists of two main parts:
- Numerator: The top number (10 in this case) represents the part of the whole we are considering.
- Denominator: The bottom number (80000) represents the total number of parts that make up the whole.
Understanding these components is crucial for interpreting the fraction's value and its significance in relation to the whole.
Converting Fractions to Decimals and Percentages
The conversion process from a fraction to a decimal and then to a percentage is a fundamental skill in mathematics. It allows us to easily compare proportions and understand their relative magnitudes. We've already demonstrated this process with 10/80000. However, let's explore the general approach:
- Fraction to Decimal: Divide the numerator by the denominator.
- Decimal to Percentage: Multiply the decimal by 100 and add a "%" sign.
Practical Applications of Proportions
The calculation of 10/80000, while seemingly simple, has far-reaching applications in various fields:
-
Statistics: Analyzing survey results, calculating probabilities, and understanding data distributions often involve working with proportions and percentages. For example, if 10 out of 80,000 respondents to a survey answered "yes" to a particular question, this represents a very low response rate.
-
Finance: Calculating interest rates, analyzing investment returns, and determining financial ratios all rely on understanding and manipulating proportions.
-
Science: In scientific experiments and data analysis, proportions are essential for interpreting results, comparing experimental groups, and establishing relationships between variables.
-
Engineering: Proportionality is crucial in scaling designs, calculating material requirements, and ensuring structural integrity.
-
Manufacturing: Quality control often involves calculating the percentage of defective products to assess production efficiency and identify areas for improvement.
Simplifying Fractions: A Helpful Technique
While the fraction 10/80000 is already relatively simple, we can further simplify it by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 10 and 80000 is 10. Dividing both the numerator and denominator by 10, we get:
10/80000 = 1/8000
This simplified fraction represents the same proportion but is easier to work with in certain contexts.
Working with Very Small Percentages: Considerations
The result of 0.0125% highlights the importance of handling very small percentages. In many situations, rounding or using scientific notation might be necessary for clarity and ease of communication. For example, it might be more practical to report this as approximately 0.01% rather than 0.0125%. The level of precision required depends entirely on the specific context.
Extending the Concept: Proportional Reasoning
The calculation of 10/80000 exemplifies the broader concept of proportional reasoning. This is the ability to understand and solve problems involving ratios and proportions. Proportional reasoning is a fundamental skill used in various aspects of life, including:
- Scaling recipes: Adjusting ingredient quantities based on the number of servings.
- Map reading: Interpreting distances and scales on maps.
- Comparing prices: Determining the best value for money when purchasing goods.
- Understanding rates: Calculating speed, unit costs, or any other rates involving two different units.
Beyond the Calculation: Developing Mathematical Fluency
The simple question, "What is 10/80000?", serves as a gateway to explore a wider range of mathematical concepts and skills. By understanding the underlying principles of fractions, decimals, percentages, and proportions, we gain the ability to solve more complex problems and apply these skills to various real-world situations. Developing mathematical fluency is crucial for critical thinking, problem-solving, and navigating the complexities of modern life.
Advanced Concepts and Further Exploration
For those interested in delving deeper, exploring the following concepts can provide a more comprehensive understanding of the mathematical underpinnings of this calculation:
-
Ratio and Proportion: Understanding the formal definitions and properties of ratios and proportions can enhance problem-solving capabilities.
-
Significant Figures: Learning about significant figures helps in determining the appropriate level of precision when presenting numerical results.
-
Scientific Notation: Using scientific notation provides a concise and efficient way to represent extremely large or small numbers.
-
Error Analysis: Understanding potential sources of error in calculations and how to minimize their impact is crucial for accuracy and reliability.
-
Statistical Inference: Applying statistical methods to analyze data and draw inferences from proportions and percentages allows for more sophisticated data interpretation.
In conclusion, while the answer to "What is 10/80000?" is a simple 0.0125%, the journey to finding this answer provides a valuable opportunity to explore fundamental mathematical concepts and their wide-ranging applications. Understanding these principles empowers us to tackle more complex problems, interpret data effectively, and make informed decisions in various aspects of life. The seemingly simple calculation opens the door to a much richer understanding of mathematics and its profound relevance to the world around us.
Latest Posts
Latest Posts
-
How Many Teaspoons In 1 Ounce
Sep 19, 2025
-
Whats Half Of 1 1 2
Sep 19, 2025
-
Highest Number On Roulette Wheel
Sep 19, 2025
-
1 2 Pint In Cups
Sep 19, 2025
-
Is Ibuprofen A Cholinergic Agent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 80000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.