What Is 15 Of 250
gasmanvison
Sep 12, 2025 · 5 min read
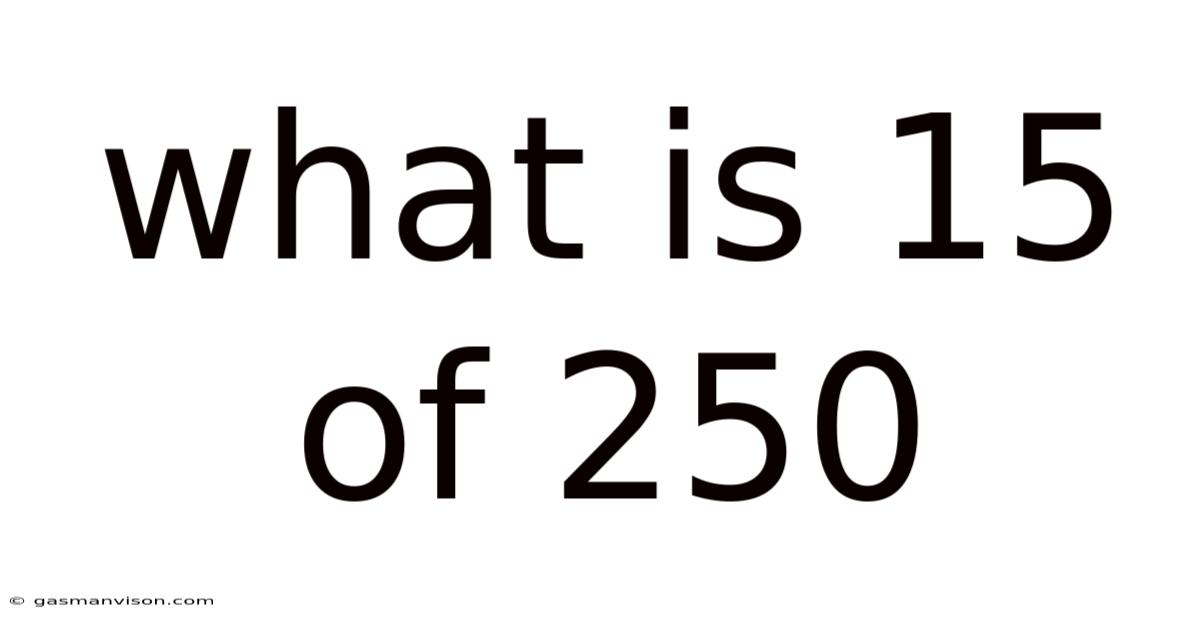
Table of Contents
What is 15% of 250? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "What is 15% of 250?", opens the door to a broader understanding of percentages, their practical applications, and the underlying mathematical principles. While a quick calculation can provide the answer, exploring the "how" and "why" behind the calculation unlocks a wealth of knowledge applicable across various fields. This article will not only answer the question but delve into the methods of calculating percentages, explore real-world examples, and demonstrate the versatility of percentage calculations.
Meta Description: Discover how to calculate 15% of 250 and explore the broader applications of percentage calculations in everyday life, finance, and more. Learn multiple methods and gain a deeper understanding of this fundamental mathematical concept.
Understanding Percentages: A Foundation
Percentages represent parts of a whole, expressed as a fraction of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Therefore, 15% can be understood as 15 out of 100, or 15/100, which simplifies to the decimal 0.15. This decimal representation is crucial for performing percentage calculations efficiently.
Calculating 15% of 250: Three Approaches
There are several ways to determine 15% of 250. Let's explore three common methods:
1. Decimal Conversion Method:
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent (15% = 0.15) and then multiply it by the number:
0.15 * 250 = 37.5
Therefore, 15% of 250 is 37.5.
2. Fraction Method:
We can express 15% as a fraction (15/100) and then multiply it by 250:
(15/100) * 250 = 37.5
This method highlights the fractional nature of percentages and provides an alternative approach to the calculation. Note that simplifying the fraction before multiplication (15/100 simplifies to 3/20) can sometimes streamline the process.
3. Proportion Method:
This method uses the concept of proportions to solve for the unknown value. We set up a proportion:
15/100 = x/250
Cross-multiplying, we get:
100x = 15 * 250
100x = 3750
x = 3750 / 100
x = 37.5
This method emphasizes the relational aspect of percentages and is particularly useful when dealing with more complex percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-life scenarios:
1. Finance:
-
Interest calculations: Banks and financial institutions use percentages to calculate interest on loans, savings accounts, and investments. Understanding percentage calculations is crucial for managing personal finances effectively. For example, calculating the interest accrued on a savings account or determining the monthly payment on a loan requires proficiency in percentage calculations.
-
Discounts and sales tax: Retailers frequently offer discounts expressed as percentages. Calculating the final price after a discount requires understanding how to subtract a percentage from the original price. Similarly, sales tax is added to the price, calculated as a percentage of the original cost. Knowing how to calculate these percentages ensures you can make informed purchasing decisions.
-
Investment returns: Investors use percentage calculations to track the performance of their investments. Understanding percentage change allows for a clear assessment of investment growth or loss over time. Analyzing percentage returns helps investors make strategic decisions about their portfolio.
-
Profit margins: Businesses use percentage calculations to determine their profit margins—the difference between the cost of goods and the selling price, expressed as a percentage of the selling price. Profit margins are crucial for evaluating business profitability and making pricing decisions.
2. Everyday Life:
-
Tip calculations: Calculating tips in restaurants is a common application of percentages. Determining a 15% or 20% tip on a bill is a simple percentage calculation.
-
Grading systems: Many educational institutions use percentages to represent grades. Understanding the percentage equivalent of a letter grade is essential for tracking academic progress.
-
Surveys and statistics: Percentages are frequently used to represent data in surveys and statistical analyses. Understanding how percentages are calculated and interpreted is crucial for drawing meaningful conclusions from data.
3. Science and Engineering:
-
Data analysis: In scientific research, percentages are used extensively to present and analyze data. For instance, expressing experimental results as percentages helps compare different treatments or conditions.
-
Engineering calculations: Percentage calculations are frequently employed in various engineering disciplines, such as determining material efficiency or calculating error margins.
4. Business and Marketing:
-
Market share analysis: Businesses use percentages to analyze their market share—the proportion of the total market that a company controls. Understanding market share is vital for strategic planning and competitive analysis.
-
Conversion rates: In online marketing, conversion rates (the percentage of website visitors who complete a desired action) are a key metric for evaluating the effectiveness of marketing campaigns. Monitoring and improving conversion rates are crucial for online business success.
-
Customer satisfaction: Businesses often use surveys to measure customer satisfaction, and the results are typically expressed as percentages. Tracking customer satisfaction helps businesses identify areas for improvement.
Beyond the Basics: Advanced Percentage Calculations
While calculating 15% of 250 is a straightforward task, more complex percentage problems often require a multi-step approach. These can include:
-
Calculating percentage increase or decrease: This involves determining the percentage change between two values. For example, if a price increases from 100 to 120, the percentage increase is calculated as [(120-100)/100] * 100% = 20%.
-
Finding the original value after a percentage change: If a price is reduced by 20% to 80, the original price can be found by solving the equation: x - 0.20x = 80.
-
Calculating percentages of percentages: This involves calculating a percentage of a percentage, which requires multiplying the two percentages together. For example, finding 10% of 25% of a number requires multiplying 0.10 by 0.25.
Mastering these advanced techniques expands the applicability of percentage calculations to even more complex scenarios.
Conclusion: The Power of Percentages
The seemingly simple question of "What is 15% of 250?" serves as a springboard to a much broader understanding of the pervasive role of percentage calculations in various aspects of life. From personal finance to scientific research, the ability to accurately and efficiently calculate percentages is a valuable skill with wide-ranging applications. By understanding the underlying mathematical principles and mastering various calculation methods, you equip yourself with a powerful tool for navigating the numerical world around you. Beyond simply finding the answer (37.5), this exploration emphasizes the importance of comprehending the process and recognizing the versatile nature of percentage calculations in numerous contexts. This knowledge provides a foundation for tackling more complex problems and making informed decisions in various fields.
Latest Posts
Latest Posts
-
2020 Practice Exam 2 Mcq
Sep 12, 2025
-
10 Percent Of A Million
Sep 12, 2025
-
Are Humans A Multicellular Organism
Sep 12, 2025
-
Lewis Structure For Snf6 2
Sep 12, 2025
-
Write 987 6 In Scientific Notation
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.